
- •2. Линейные дифференциальные уравнения
- •2.1. Линейные однородные дифференциальные уравнения 2-го порядка
- •2.2. Линейные однородные дифференциальные уравнения n-го порядка
- •2.3. Метод вариации произвольных постоянных решения неоднородных дифференциальных уравнений
- •2.4. Линейные неоднородные дифференциальные уравнения 2-го порядка с правой частью вида
- •2.5. Линейные неоднородные дифференциальные уравнения 2-го порядка с правой частью вида
- •2.6. Линейные неоднородные дифференциальные уравнения 3-го и 4-го порядков со специальной правой частью
- •2.7. Применение дифференциальных уравнений 2-го порядка для решения геометрических задач
- •2.8. Применение дифференциальных уравнений 2-го порядка для решения физических задач
- •2.9. Однородные и неоднородные уравнения Эйлера
2.7. Применение дифференциальных уравнений 2-го порядка для решения геометрических задач
Из курса
математического анализа известно, что
производная
![]() функции
функции![]() применяется для исследования геометрических
свойств линий, а именно: выпуклость
(вверх и вниз) и кривизна линии. Кривизна
линии характеризует скорость вращения
касательной к кривой при движении точки
по кривой.
применяется для исследования геометрических
свойств линий, а именно: выпуклость
(вверх и вниз) и кривизна линии. Кривизна
линии характеризует скорость вращения
касательной к кривой при движении точки
по кривой.
Пусть
![]() есть угол, на который поворачивается
касательная при переходе из точки
есть угол, на который поворачивается
касательная при переходе из точки![]() кривой линии
кривой линии![]()
![]() в точку
в точку![]() ,
а
,
а![]() − длина части кривой между названными
точками. Тогда величина
− длина части кривой между названными
точками. Тогда величина![]() выражает среднюю кривизну дуги
выражает среднюю кривизну дуги![]() .
Величина
.
Величина![]() =
=![]() называется кривизной кривой
называется кривизной кривой![]() ,
а величина
,
а величина![]() радиусом кривизны кривой
радиусом кривизны кривой![]() в точке
в точке![]() .
.
Для окружности
кривизна величина постоянная и равна
![]() ,
где
,
где![]() – радиус окружности. Чем меньше радиус,
тем больше кривизна. Последнюю формулу
легко получить из того, что длина
– радиус окружности. Чем меньше радиус,
тем больше кривизна. Последнюю формулу
легко получить из того, что длина![]() любой дуги окружности равна
любой дуги окружности равна![]() ,
где
,
где![]() − радиус окружности,
− радиус окружности,![]() – центральный угол, опирающийся на дугу
(центральный угол, опирающийся на дугу
окружности равен углу между касательными,
проведенными к дуге окружности в её
концах).
– центральный угол, опирающийся на дугу
(центральный угол, опирающийся на дугу
окружности равен углу между касательными,
проведенными к дуге окружности в её
концах).
Н а
рис.2.1 показана окружность радиуса
а
рис.2.1 показана окружность радиуса![]() для точки
для точки![]() кривой. Учитывая смысл предельного
перехода, заметим, что кривую
кривой. Учитывая смысл предельного
перехода, заметим, что кривую![]() в окрестности точки
в окрестности точки![]() можно заменить соприкасающейся
окружностью радиуса
можно заменить соприкасающейся
окружностью радиуса![]() .
Центр этой окружности располагается
на нормали кривой в данной точке, причём
в той же полуплоскости относительно
касательной, что и рассматриваемая
кривая.
.
Центр этой окружности располагается
на нормали кривой в данной точке, причём
в той же полуплоскости относительно
касательной, что и рассматриваемая
кривая.
В
математическом анализе для вычисления
кривизны линии в каждой её точке получена
формула
![]() =
=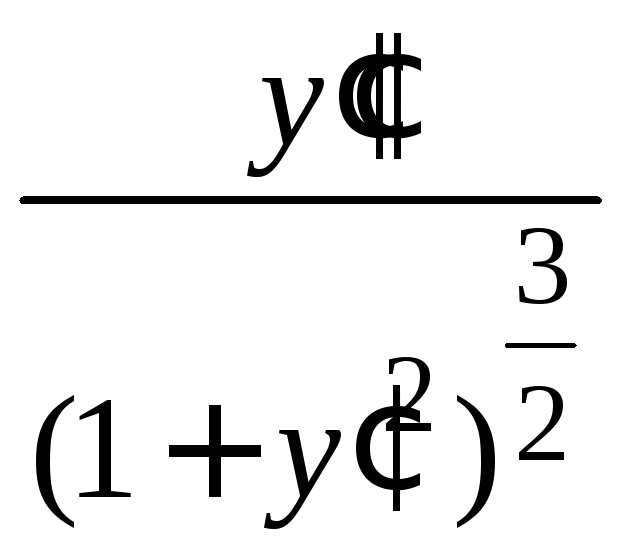 .
Это значит, что радиус кривизны
.
Это значит, что радиус кривизны![]() =
=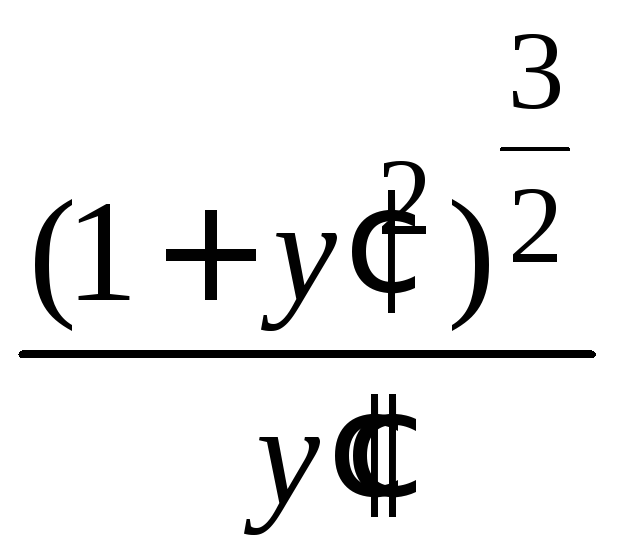 .
.
Известно,
что для линий, выпуклых вниз, производная
![]() >0.
Для таких линий
>0.
Для таких линий![]() и
и![]() ,
что согласуется с чертежом. Соответственно,
для линий, выпуклых вверх −
,
что согласуется с чертежом. Соответственно,
для линий, выпуклых вверх −![]() и
и![]() .
Учитывая замеченное свойство кривых
линий, удобно определить проекцию
радиуса кривизны на ось
.
Учитывая замеченное свойство кривых
линий, удобно определить проекцию
радиуса кривизны на ось![]() формулой
формулой![]() =
=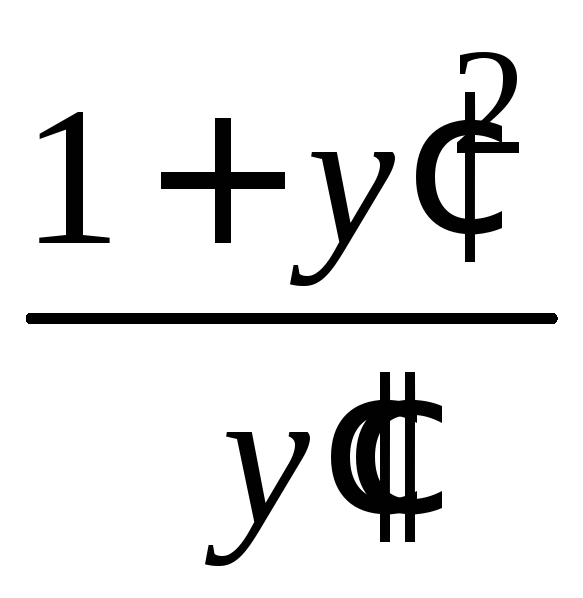 ,
что отражает направление радиуса
кривизны вдоль нормали кривой для
рассматриваемой точки.
,
что отражает направление радиуса
кривизны вдоль нормали кривой для
рассматриваемой точки.
Пример 2.12.Найти уравнение линии, для которой
проекция радиуса кривизны на ось![]() равна 1.
равна 1.
Решение.
1)
Учитывая условие задачи:
![]() =1,
запишем дифференциальное уравнение,
соответствующее требуемым геометрическим
свойствам линии или
=1,
запишем дифференциальное уравнение,
соответствующее требуемым геометрическим
свойствам линии или![]() .
.
2)
Дифференциальное уравнение
![]() решаем способом понижения порядка,
принимая
решаем способом понижения порядка,
принимая![]() =
=![]() .
Тогда
.
Тогда![]() .
Перепишем уравнение
.
Перепишем уравнение![]() ,
или
,
или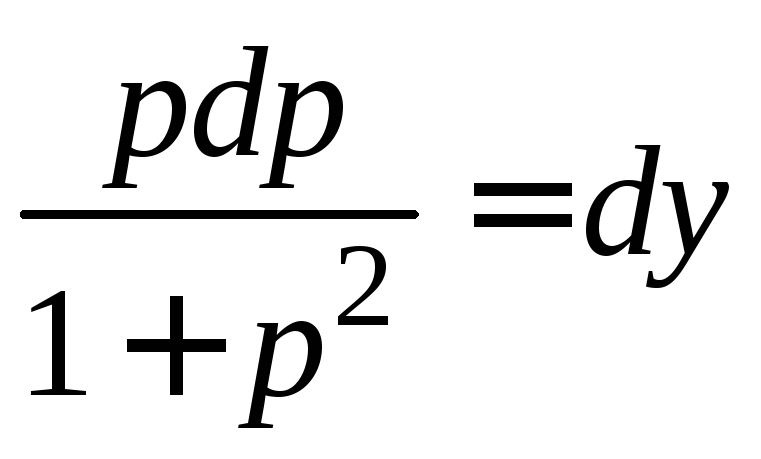 .
Интегрируя это уравнение, получаем
.
Интегрируя это уравнение, получаем![]() ,
или
,
или![]() .
.
3) Так
как
![]() =
=![]() ,
из выражения
,
из выражения![]() следует
следует![]() .
Учитывая, что
.
Учитывая, что![]() =
=![]() ,
получим уравнение
,
получим уравнение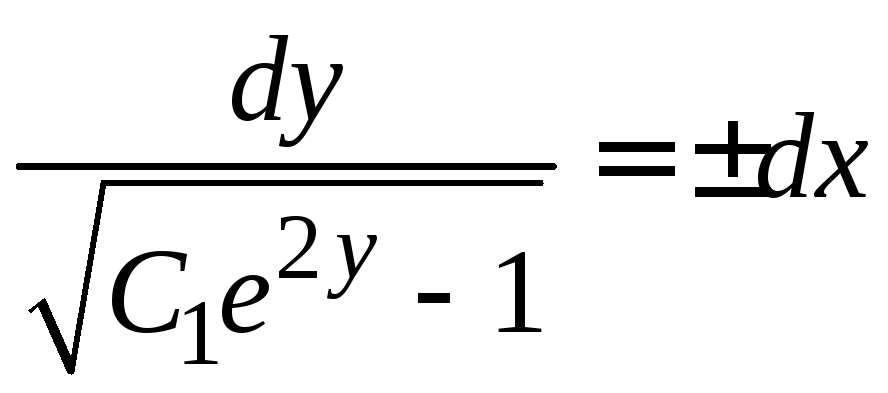 .
При вычислении интеграла левой части
применяем способ замены переменных. В
результате получим
.
При вычислении интеграла левой части
применяем способ замены переменных. В
результате получим![]() .
.
Замечание.
Выражение общего решения можно
преобразовать к виду более удобному
для применения в задачах Коши
![]() .
.
Ответ.
![]() ,
или
,
или
![]() .
.
Задание 2.7. Найти уравнения кривых.
Замечания. 1) При раскрытии модулей можно ограничиться случаем положительности выражений, стоящих под знаком модуля.
2) Для
решения получаемых в заданиях уравнений
2-го порядка нужно будет использовать
методы понижения порядка уравнения.
Далее потребуется применение способов
решения уравнения
![]() ,
не разрешённого относительно производной.
В записи решения этого уравнения могут
содержаться неопределенные интегралы,
если их вычисление является сложным.
,
не разрешённого относительно производной.
В записи решения этого уравнения могут
содержаться неопределенные интегралы,
если их вычисление является сложным.
2.7.1.Найти
уравнение линии, для которой проекция
радиуса кривизны на ось![]() для
всех её точек сохраняет постоянное
значение, равное –1.
для
всех её точек сохраняет постоянное
значение, равное –1.
2.7.2.Найти уравнение линии, для которой радиус кривизны в любой её точке равен длине нормали.
2.7.3.Найти уравнение линии, для которой радиус кривизны в любой её точке равен длине касательной.
2.7.4.Найти
уравнение линии, для которой проекция
радиуса кривизны на ось![]() для
всех её точек сохраняет постоянное
значение, равное 2.
для
всех её точек сохраняет постоянное
значение, равное 2.
2.7.5.Найти
уравнение линии, для которой радиус
кривизны в любой её точке определяется
зависимостью:![]() =
=![]() [длина
нормали], если
[длина
нормали], если![]() .
.
2.7.6.Найти
уравнение линии, для которой радиус
кривизны в любой её точке определяется
зависимостью:![]() =
=![]() [длина
касательной], если
[длина
касательной], если![]() .
.
2.7.7.Найти
уравнение линии, для которой проекция
радиуса кривизны на ось![]() для
всех её точек сохраняет постоянное
значение, равное –2.
для
всех её точек сохраняет постоянное
значение, равное –2.
2.7.8.Найти
уравнение линии, для которой радиус
кривизны в любой её точке определяется
зависимостью:![]() =
=![]() [длина
нормали], если
[длина
нормали], если![]() .
.
2.7.9.Найти
уравнение линии, для которой радиус
кривизны в любой её точке определяется
зависимостью:![]() =
=![]() [длина
касательной], если
[длина
касательной], если![]() .
.
2.7.10.Найти
уравнение линии, для которой проекция
радиуса кривизны на ось![]() для
всех её точек сохраняет постоянное
значение, равное 3.
для
всех её точек сохраняет постоянное
значение, равное 3.
