
- •2. Линейные дифференциальные уравнения
- •2.1. Линейные однородные дифференциальные уравнения 2-го порядка
- •2.2. Линейные однородные дифференциальные уравнения n-го порядка
- •2.3. Метод вариации произвольных постоянных решения неоднородных дифференциальных уравнений
- •2.4. Линейные неоднородные дифференциальные уравнения 2-го порядка с правой частью вида
- •2.5. Линейные неоднородные дифференциальные уравнения 2-го порядка с правой частью вида
- •2.6. Линейные неоднородные дифференциальные уравнения 3-го и 4-го порядков со специальной правой частью
- •2.7. Применение дифференциальных уравнений 2-го порядка для решения геометрических задач
- •2.8. Применение дифференциальных уравнений 2-го порядка для решения физических задач
- •2.9. Однородные и неоднородные уравнения Эйлера
2.2. Линейные однородные дифференциальные уравнения n-го порядка
Для решения
однородных дифференциальных уравнений
с постоянными коэффициентами
n-го
порядка
![]() применяют описанный в п.2.1. алгоритм
решения уравнений 2-го порядка, то есть
записывают характеристическое уравнение
применяют описанный в п.2.1. алгоритм
решения уравнений 2-го порядка, то есть
записывают характеристическое уравнение![]() и находят его корни. Необходимо лишь
учесть, что:
и находят его корни. Необходимо лишь
учесть, что:
каждому действительному корню
 кратности
кратности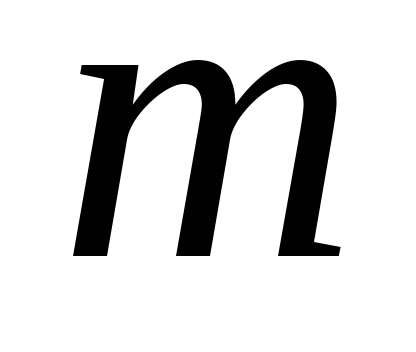 характеристического уравнения
соответствует
характеристического уравнения
соответствует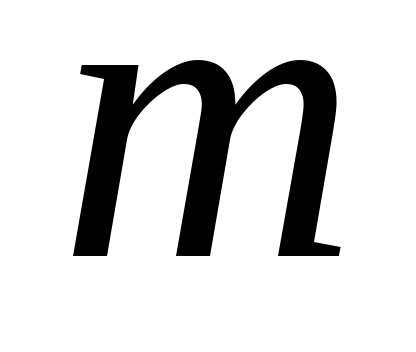 решений в ФСР:
решений в ФСР: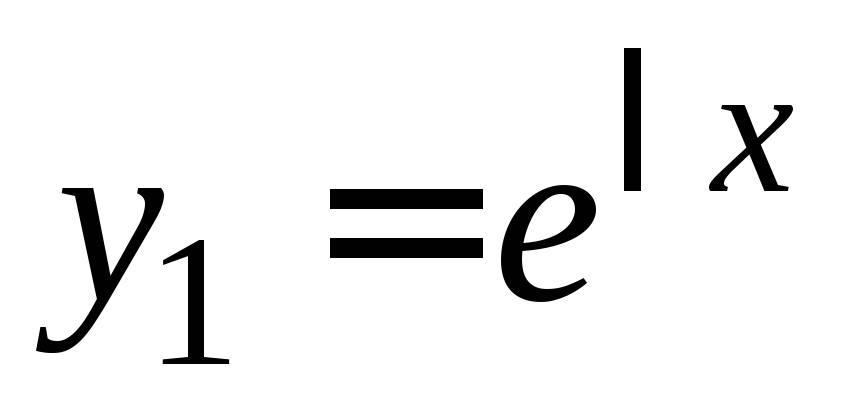 и
и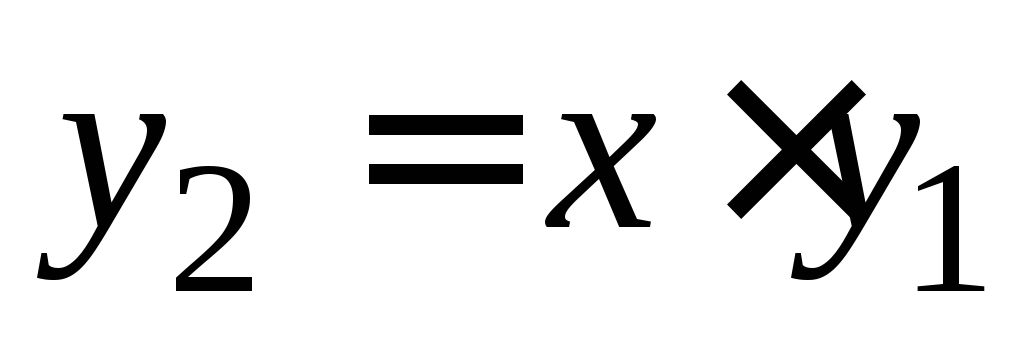 ,
…,
,
…,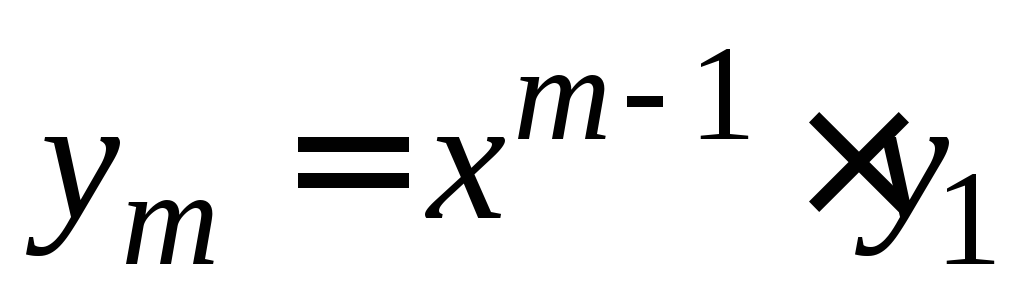 ;
;каждой паре комплексных корней
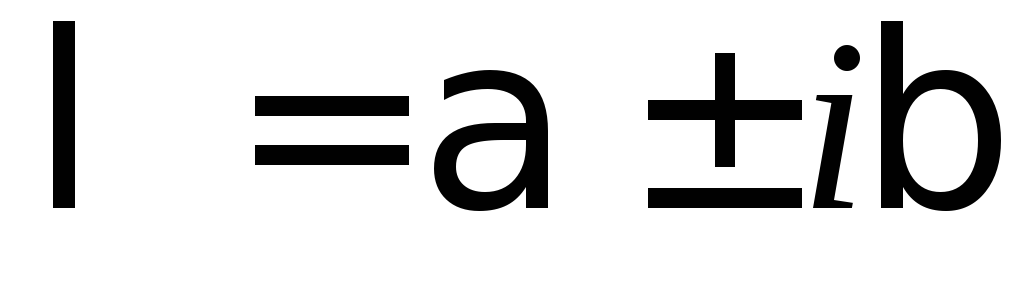 кратности
кратности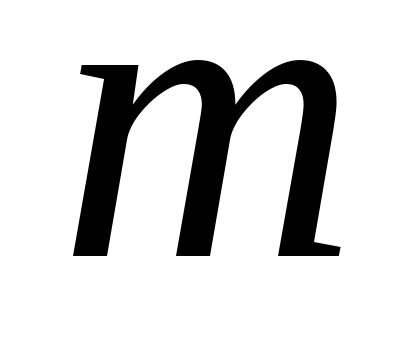 характеристического уравнения
соответствует
характеристического уравнения
соответствует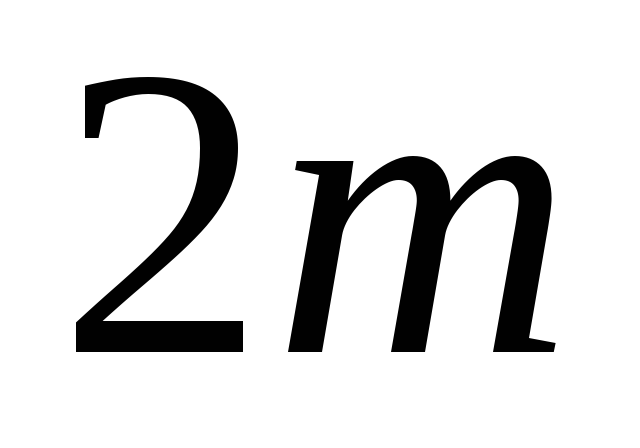 решений в ФСР:
решений в ФСР: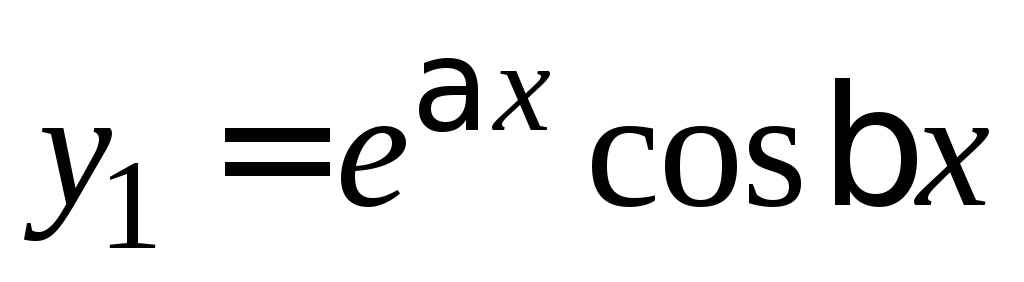 ,
,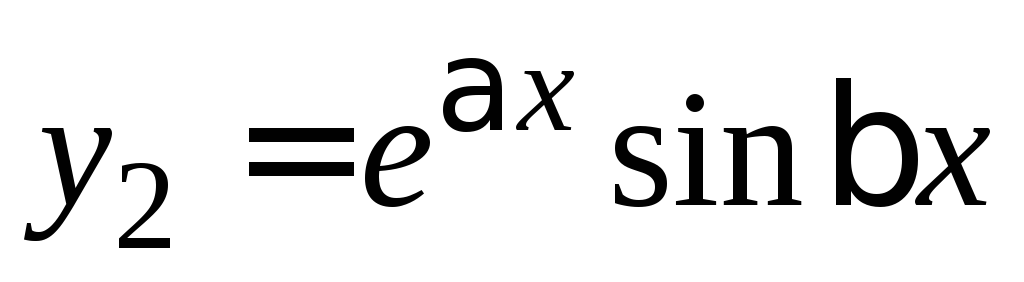 ,
,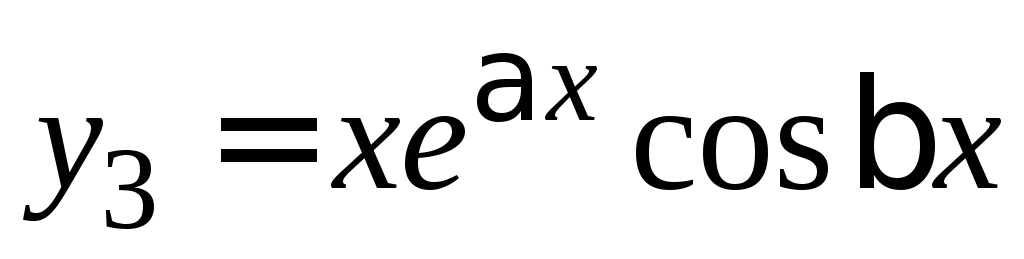 ,
,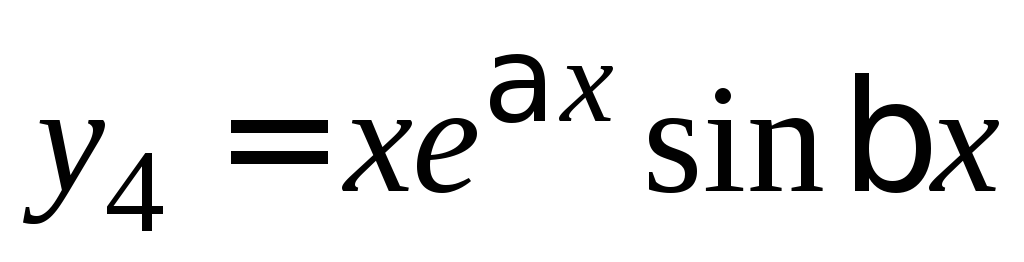 ,…,
,…,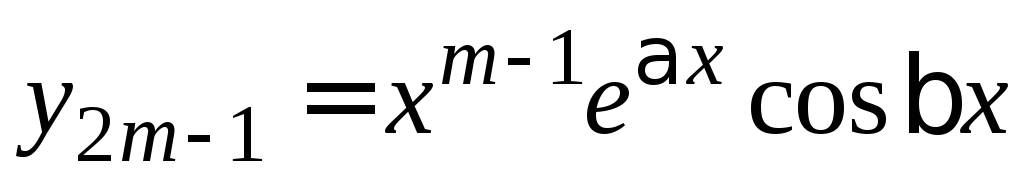 ,
,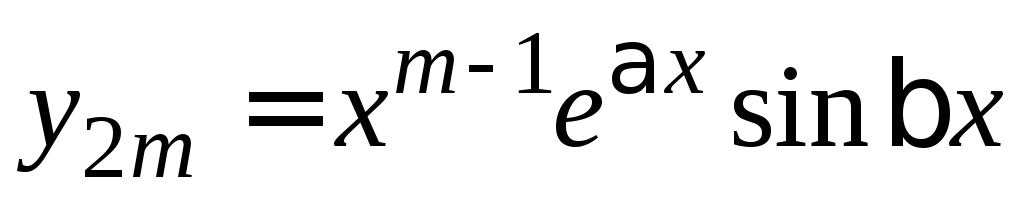 .
.
Задание 2.2. Найти общие решения уравнений.
|
Вар. |
Уравнение |
Вар. |
Уравнение |
|
2.2.1. |
|
2.2.16. |
|
|
2.2.2. |
|
2.2.17. |
|
|
2.2.3. |
|
2.2.18. |
|
|
2.2.4. |
|
2.2.19. |
|
|
2.2.5. |
|
2.2.20. |
|
|
2.2.6. |
|
2.2.21. |
|
|
2.2.7. |
|
2.2.22. |
|
|
2.2.8. |
|
2.2.23. |
|
|
2.2.9. |
|
2.2.24. |
|
|
2.2.10. |
|
2.2.25. |
|
|
2.2.11. |
|
2.2.26. |
|
|
2.2.12. |
|
2.2.27. |
|
|
2.2.13. |
|
2.2.28. |
|
|
2.2.14. |
|
2.2.29. |
|
|
2.2.15. |
|
2.2.30. |
|
2.3. Метод вариации произвольных постоянных решения неоднородных дифференциальных уравнений
Для решения линейных неоднородных дифференциальных уравнений может быть использован метод вариации произвольных постоянных. Опишем его алгоритм на примере неоднородного дифференциального уравнения с постоянными коэффициентами 2-го порядка.
1) Для заданного
уравнения
![]() запишем соответствующее ему однородное
дифференциальное уравнение
запишем соответствующее ему однородное
дифференциальное уравнение
![]() . (2.1)
. (2.1)
2) Находим общее
решение данного однородного уравнения:
![]() ,
где
,
где![]() и
и![]() – функции ФСР, а
– функции ФСР, а![]() и
и![]() – произвольные постоянные.
– произвольные постоянные.
3) Заменим постоянные
![]() и
и![]() на функции
на функции![]() и
и![]() ,
причём так, что функция
,
причём так, что функция![]() будет уже решением неоднородного
уравнения.
будет уже решением неоднородного
уравнения.
4) Найдём производную
![]() для функции
для функции![]() :
:![]() =
=![]() +
+![]() и потребуем
и потребуем
![]() =0, (2.2)
=0, (2.2)
то есть, чтобы
производная
![]() имела такой же вид, как и при постоянных
имела такой же вид, как и при постоянных![]() и
и![]() .
.
5) Учитывая (2.2),
найдём производную
![]() .
Получаем
.
Получаем![]() =
=![]() +
+![]() .
.
6) Подставив
![]() ,
,![]() и
и![]() в исходное уравнение и учитывая, что
в исходное уравнение и учитывая, что![]() и
и![]() являются решениями однородного
уравнения, получаем ещё одно требование
к функциям
являются решениями однородного
уравнения, получаем ещё одно требование
к функциям![]() и
и![]()
![]() =
=![]() . (2.3)
. (2.3)
7) Из условий (2.2) и (2.3) составляем систему:
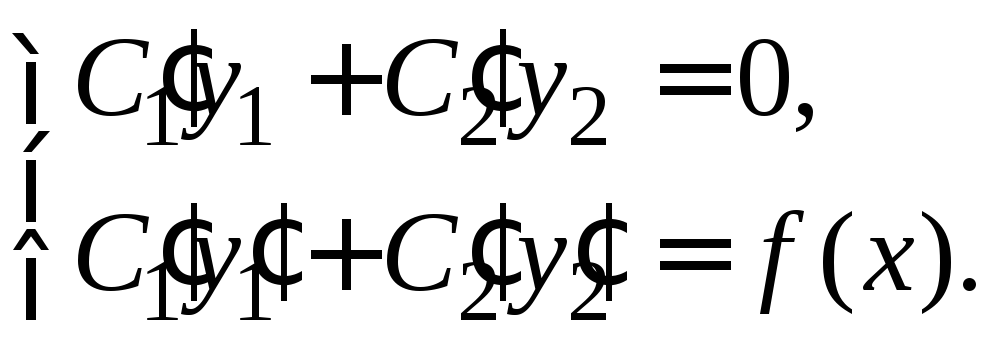 (2.4)
(2.4)
8) Из системы (2.4)
нетрудно получить выражения:
![]() и
и![]() ,
которые затем интегрируем:
,
которые затем интегрируем:
![]() и
и![]() . (2.5)
. (2.5)
В выражении (2.5)
величины
![]() и
и![]() – произвольные постоянные.
– произвольные постоянные.
9) Используя (2.5),
то есть выражения для функций
![]() и
и![]() ,
записываем общее решение неоднородного
уравнения:
,
записываем общее решение неоднородного
уравнения:
![]() . (2.6)
. (2.6)
Из (2.6) следует, что
общее решение неоднородного уравнения
представляется в виде
![]() ,
где
,
где![]() – общее решение однородного уравнения
(2.1), а функция
– общее решение однородного уравнения
(2.1), а функция![]() =
=![]() – частное решение неоднородного
уравнения.
– частное решение неоднородного
уравнения.
Пример 2.3.Решить задачу Коши![]() ,
,![]() ,
,![]() ,
применив метод вариации произвольных
постоянных.
,
применив метод вариации произвольных
постоянных.
Решение: 1)
Составляем характеристическое уравнение![]() .
.
2) Характеристические
корни уравнения:
![]() .
ФСР:
.
ФСР:![]() и
и![]() .
Составим общее решение однородного
уравнения:
.
Составим общее решение однородного
уравнения:![]() =
=![]() .
.
3) Составим систему:
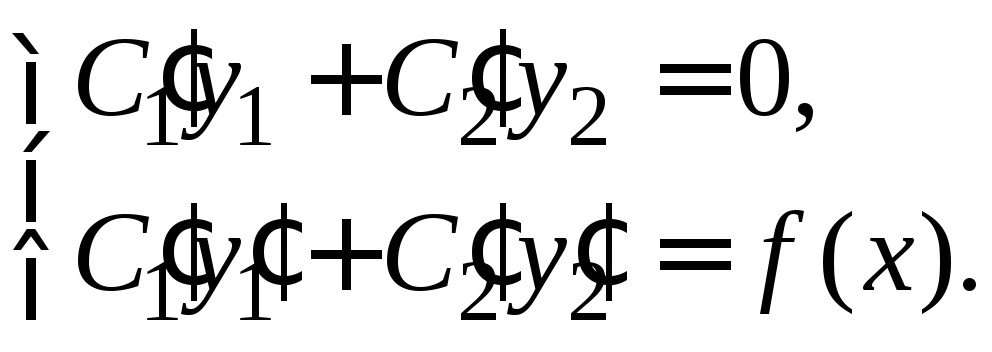 В нашем случае:
В нашем случае: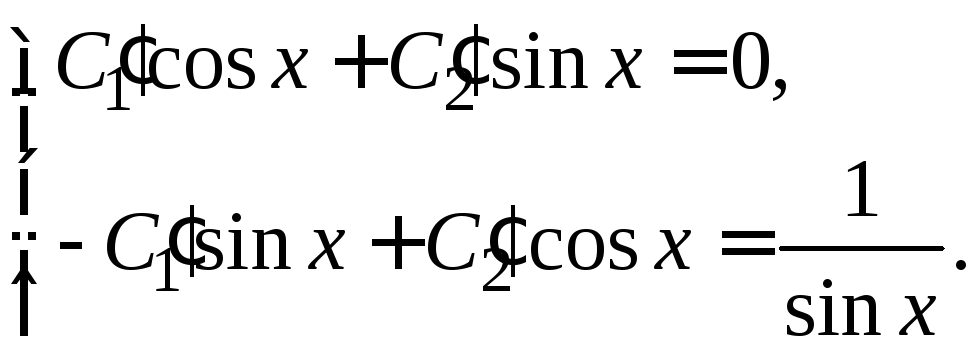 Из этой системы получаем
Из этой системы получаем![]() и
и![]() .
.
4) Вычислим:
![]() =
=![]() и
и![]() =
=![]() =
=![]() .
Составим частное решение неоднородного
уравнения
.
Составим частное решение неоднородного
уравнения
![]() =
=![]() =
=![]() .
.
5) Составим общее
решение неоднородного уравнения
![]() .
.
6) Для заданных
начальных условий получаем
![]() ,
,![]() .
.
Ответ:Общее
решение:![]()
![]() ,частное решение:
,частное решение:![]()
![]() .
.
Задание 2.3. Решить задачу Коши, применяя метод вариации произвольных постоянных.
|
Вар. |
Уравнение |
Начальные условия |
|
2.3.1 |
|
|
|
2.3.2. |
|
|
|
2.3.3. |
|
|
|
2.3.4. |
|
|
|
2.3.5. |
|
|
|
2.3.6. |
|
|
|
2.3.7. |
|
|
|
2.3.8. |
|
|
|
2.3.9. |
|
|
|
2.3.10. |
|
|
|
2.3.11. |
|
|
|
2.3.12. |
|
|
|
2.3.13. |
|
|
|
2.3.14. |
|
|
|
2.3.15. |
|
|
|
2.3.16. |
|
|
|
2.3.17. |
|
|
|
2.3.18. |
|
|
|
2.3.19. |
|
|
|
2.3.20. |
|
|
|
2.3.21. |
|
|
|
2.3.22. |
|
|
|
2.3.23. |
|
|
|
2.3.24. |
|
|
|
2.3.25. |
|
|
|
2.3.26. |
|
|
|
2.3.27. |
|
|
|
2.3.28. |
|
|
|
2.3.29. |
|
|
|
2.3.30. |
|
|
