Примеры показывают, что правила обеспечивают последовательность в преобразовании формул, каждая из которых есть либо аксиома, либо посылка, либо промежуточный результат и, наконец, заключение.

1.1.2.4. Метод резолюции

Существует эффективный алгоритм логического вы-

вода - принцип (или метод) резолюции Дж. Робинсона.

Он показал, что выводимость формулы В из множества посылок и аксиом F1, F2, F3, …, Fn равносильна доказательству теоремы:

| (F1&F2&F3&. . .&Fn→B),

| (¬(F1&F2&F3&. . .&Fn) B), | ¬(F1&F2&F3&. . .&Fn&¬B).

Из последней формулы следует, что заключение В истинно тогда и только тогда, когда формула

(F1&F2&F3&...&Fn&( B))=л. Так как

(F1&F2&F3&...&Fn&( B)) есть КНФ, то все Fi и B должны быть приведены также к виду КНФ. Так может быть

сформировано множество элементарных дизъюнктов К={D1, D2, …, Dm}. Два дизъюнкта Di и Dj, содержащие одинаковые пропозициональные переменные, но с противоположными знаками, объединяют в третий дизъюнкт Dk=(Di Dj)– резольвенту , из которой удаляются эти переменные. Пропозициональные переменные с противоположными знаками называют контрарными атомами. Ес-

ли Di=А, Dj=¬A, то Dk=(Di Dj)=(А ¬A) есть пустая резольвента, которую обозначают символом . Многократно применяя процедуру объединения дизъюнктов множества K с контрарными атомами стремятся получить пустую ре-

зольвенту. Наличие пустой резольвенты есть решение

| (F1&F2&F3&...&Fn& B).

Алгоритм вывода по методу резолюции:

Шаг 1: принять отрицание заключения, т.е. ¬В, Шаг 2: привести все формулы посылок и отрицания

заключения в конъюнктивную нормальную форму, Шаг 3: выписать множество дизъюнктов всех посы-

лок и отрицания заключения: K = {D1, D2, …, Dk },

Шаг 4: выполнить анализ пар множества K по прави-

лу:

«если существуют дизъюнкты Di и Dj, один из которых (Di) содержит атом А, а другой (Dj) - атом ¬А, то соединить эту пару логической связкой дизъюнкции (Di Dj) и сформировать новый дизъюнкт - резольвенту, исключив контрарные атомы А и ¬А, а резольвенту включить в множество К»,

Шаг 5: если в результате соединения дизъюнктов будет получена пустая резольвента (пустой дизъюнкт), то конец (доказательство подтвердило истинность заключения), иначе включить резольвенту в множество дизъюнктов K и перейти к шагу 4; по закону идемпотентности любой дизъюнкт и любую резольвенту можно использовать неоднократно, т.е. из множества К не следует удалять использованные в соединении дизъюнкты.

Пример 1.43. Доказать истинность заключения по ме-

тоду резолюции: (A & B →C),(C& D →¬M),(¬N → D& M) (A & B → N).

Вывод по методу резолюции:

• A&B→C≡¬(A&B) C≡(¬A ¬B C) – посылка содер-

жит один дизъюнкт,

•C&D→¬M≡¬(C&D) ¬M≡(¬C ¬D ¬M) – посылка содержит один дизъюнкт,

•¬N→D&M≡¬¬N D&M≡(N D)&(N M) – посылка со-

держит два дизъюнкта,

•¬((A&B)→N)≡A&B&¬N - отрицание заключения содержит три одно-литерных дизъюнкта,

•множество дизъюнктов:

K={(¬A ¬B C), (¬C ¬D ¬M), (N D), (N M), A, B, ¬N},

•(M N) ¬N ≡ М - резольвента,

•множество дизъюнктов:

K1={(¬A ¬B C), (¬C ¬D ¬M), (N D), (N M), A, B, M, ¬N},

•(¬C ¬D ¬M) M ≡ (¬C ¬D) - резольвента,

•множество дизъюнктов:

K2={(¬A ¬B C), (¬C ¬D ¬M), (N D), (N M),A, B, M, ¬N, (¬C ¬D)},

•(¬A ¬B C) (¬C ¬D) ≡ (¬A ¬B ¬D) – резольвента,

•множество дизъюнктов:

K3={(¬A ¬B C), (¬C ¬D ¬M), (N D), (N M), A, B, M, ¬N, (¬C ¬D), (¬A ¬B ¬D)},

•(¬A ¬B ¬D) A ≡ (¬B ¬D) - резольвента,

•множество дизъюнктов:

K4={(¬A ¬B C), (¬C ¬D ¬M), (N D), (N M), A, B, M, ¬N, D, (¬C ¬D), (¬A ¬B ¬D)}, (¬B ¬D) },

•(¬B ¬D) B ≡ ¬D - резольвента,

•множество дизъюнктов:

K5={(¬A ¬B C), (¬C ¬D ¬M), (N D), (N M), A, B, M,

¬N, D, (¬C¬D), ( A B D)}, ( B D), D},

•D (N D) ≡ N - резольвента,

•множество дизъюнктов:

K6={( A B C), ( C D M), (N D), (N M), A, B, M, N, D, ( C D), (¬A¬B¬D)}, (¬B¬D), ¬D, N},

• N¬N ≡ - пустая резольвента, ч.т.д.

Для демонстрации удобно использовать граф типа дерево, корнем которого является один из дизъюнктов отрицания заключения, а листьями– дизъюнкты всех посылок и отрицания заключения. Тогда узлами графа являются резольвенты. На рис. 1.8 показан граф вывода этой задачи.

Пример 1.44. Доказать истинность заключения:

(A → B) & (C → D),(D & B → M),¬M

(¬A ¬C).

Вывод по методу резолюции:

•(A→B)&(C→D) ≡ (¬A B)&(¬C D) - посылка,

•D&B→M ≡ ¬(D&B) M ≡ (¬D ¬B M) - посылка,

•¬M - посылка,

•¬(¬A ¬C ) ≡ A &C - отрицание заключения,

•множество дизъюнктов:

K={A, C, ¬M, (¬A B), (¬C D), (¬D ¬B M)},

•A (¬A B) ≡ B - резольвента,

•множество дизъюнктов:

K={A, C, ¬M, (¬A B), (¬C D), (¬D ¬B M), B},

•B (¬D ¬B M) ≡ (¬D M) - резольвента,

•множество дизъюнктов:

K={A, C, ¬M, (¬A B), (¬C D), (¬D ¬B M), B, (¬D M)},

•(¬D M) (¬C D) ≡ (¬C M) - резольвента,

•множество дизъюнктов:

K={A, C, ¬M, (¬A B), (¬C D), (¬D ¬B M), B, (¬D M), (¬C M)},

•(¬C M) ¬M ≡ ¬C - резольвента,

•¬C C ≡ - пустая резольвента, ч.т.д.

На рис. 1.9 показан граф вывода этой задачи.

Пример 1.45. Доказать истинность заключения:

((¬A ¬B ¬A &¬B) → C),((A B A & B) →¬C)

(C →¬A).

Вывод по методу резолюции:

•((¬А ¬B ¬А &¬B)→С)≡(А C)&(B C) - посылка,

•(A B А&B)→¬C)≡(¬А ¬C)&(¬B ¬C) -посылка,

•¬(C→¬A)≡C&А – отрицание заключения,

•множество дизъюнктов:

K={(А C), (B C), (¬А ¬C), (¬B ¬C), C, А },

•С (¬А ¬C) = ¬А – резольвента,

•множество дизъюнктов:

K1={(А C), (B C), (¬А ¬C), (¬B ¬C), C, А, ¬А },

•¬А (А C) = C – резольвента,

•множество дизъюнктов:

K2={(А C), (B C), (¬А ¬C), (¬B ¬C), C, А, ¬А },

•С (¬B ¬C) = ¬B –резольвента,

•множество дизъюнктов:

K3={(А C), (B C), (¬А ¬C), (¬B ¬C), C, А, ¬А, ¬B },

•¬B (B C) = C – резольвента,

•множество дизъюнктов:

K4={(А C), (B C), (¬А ¬C), (¬B ¬C), C, А, ¬А, ¬B },

•C ¬A = (C ¬A) – резольвента,

•множество дизъюнктов:

K5={(А C), (B C), (¬А ¬C), (¬B ¬C), C, А, ¬А, ¬B, (C A)},

•(C ¬A) (¬А ¬C) = ¬А – резольвента,

•множество дизъюнктов:

K5={(А C), (B C), (¬А ¬C), (¬B ¬C), C, А, ¬А, ¬B, (C A)},

•(C ¬A) (¬А ¬C) = ¬А – резольвента,

•¬А A = - пустая резольвента, ч.т.д.

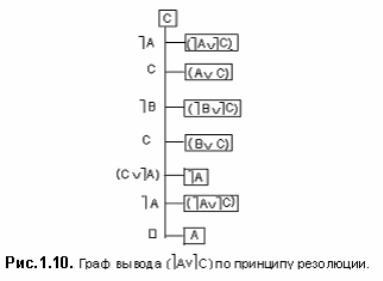
На рис. 1.10 показан граф вывода этой задачи. Обратите внимание, уже после формирования первой

резольвенты (¬А) из дизъюнктов второй посылки и отрицания заключения среди множества дизъюнктов появились два контрарных дизъюнкта (А и ¬А), соединение которых формирует пустую резольвенту. Следовательно, первая посылка - излишняя в доказательстве истинности заключения. Это подтверждается истинностью дизъюнкта (¬А ¬C), что равносильно истинности (С→¬А). Однако, в настоящем выводе был продолжен поиск решения при наличии дизъюнктов первой посылки. Так как резольвен-

ты включаются в множество дизъюнктов, то возможно их многократное использование в процессе вывода. Это оправдано законом идемпотентности, т. е. Di=Di&Di&...&Di.. Достоинством принципа резолюции является то, что при доказательстве применяют только одно правило: поиск и удаление контрарных атомов дизъюнктов, а для этого механизм вывода использует правила подстановки и унификации дизъюнктов.