5.4. Нахождение критических точек

Критические точки являются границами критических областей. Поэтому для полного задания критических областей достаточно найти их граничные (критические) точки.

Задача нахождения критических точек максимально облегчена для пользователя. Критические точки не нужно вычислять: они находятся из соответствующих таблиц.

Помещенные в таблицы критические точки рассчитаны, исходя из требования: если нулевая гипотеза H₀ с вероятностью γ верна, то получаемые в опыте значенияK_н должны с этой вероятностью γ попадать в область принятия гипотезы. Вероятность γ принято брать достаточно большой (близкой к 1). Сказанное можно выразить другими словами: если нулевая гипотезаH₀ с вероятностью γ верна, то с вероятностью α = 1 - γ наблюдаемые значения критерияK_н должны попадать в критическую область. Вероятность α называютуровнем значимости. По своему смыслу α есть вероятность того, что в результате проверки будет отвергнута правильная гипотеза. Проверку статистических гипотез принято проводить, задавая не вероятность γ, а некоторое достаточно малое (близкое к нулю) значение уровня значимости α . Наиболее часто уровень значимости принимают равным 0,01 или 0,05. Если, например, уровень значимости выбран равным 0,01, то в среднем в одной из ста проводимых по одинаковой схеме проверок будет отвергнута правильная гипотеза.

Правосторонняя критическая область состоит из таких значений критерия K, которые удовлетворяют неравенствуK>k_кр , приk_кр > 0. Поэтомуk_крдля правосторонних критических областей рассчитаны, исходя из требования, чтобы (при условии справедливости нулевой гипотезы) вероятность выполнения неравенстваK>k_крбыла равна заданному малому уровню значимости α :

Р(K >k_кр ) = α .

Критические точки левосторонних критических областей рассчитаны, исходя из требования, чтобы (при условии справедливости нулевой гипотезы) вероятность выполнения неравенства K<k_кр(k_кр< 0) была равна выбранному малому уровню значимости α :

Р(K <k_кр ) = α .

Двусторонняя критическая область состоит из двух множеств, определяемых неравенствами: K<k_кр1 иK>k_{кр 2} . Для этой области критические точки должны были бы (при условии справедливости нулевой гипотезы) находиться из уравнения:

Р(K <k_{кр 1}) +Р(K >k_{кр 2}) = α . (5.1)

Существует бесконечно много пар (k_{кр 1},k_{кр 2} ), удовлетворяющих этому уравнению, поэтому в обычных прикладных задачах такие случаи не рассматривают. Если же значения критерия распределены симметрично относительно нуля, то и критические точки можно взять симметричными: -k_кр1=k_{кр 2} =k_кр. В этом случае вместо (5.1)

получаем

Р(K < -k_кр ) +Р(K >k_кр ) = α ,

а так как

Р(K < -k_кр) =Р(K >k_кр),

то критические точки для двусторонней критической области рассчитаны из уравнения

Р(K >k_кр) = α / 2.

5.5. Проверка гипотезы о равенстве двух средних значений нормальных генеральных совокупностей

Пусть изучаются две генеральные совокупности биологических объектов, в одной из которых измеряется признак X , а в другой признакY .Пусть на основании прошлых измерений и проверок можно ожидать, что генеральные средниеM(X) иM(Y) этих совокупностей равны между собой. Другими словами, пусть можно ожидать, что и новая проверка нулевой гипотезыН₀ :M(X) =M(Y) покажет, что эта гипотеза вновь должна быть принята.

Строгая проверка данной гипотезы может быть проведена, если признаки X иY распределены нормально и дисперсии их известны. Однако в практике статистического анализа оба эти условия выполняются редко. Как правило, встречаются следующие случаи:

1) распределение значений признаков X иY по всей генеральной совокупности является нормальным (и всегда будет нормальным, хотя у каждого отдельного объекта совокупности величина признака изменяется во времени), а дисперсии признаков неизвестны;

2) распределения значений признаков X иY в генеральных совокупностях не являются нормальными и дисперсии их неизвестны.

Условия строгой проверки Н₀ можно выполнить с достаточно большой точностью. Пусть из генеральных совокупностейX иY извлечены независимые выборки объемовn и m и по этим выборкам найдены выборочные средние_в и_в . Если независимые выборки имеют большой объем (n > 30,m > 30), то выборочные средние_в и_в можно рассматривать как значения случайных величини, которые (это можно доказать) распределены приближенно нормально. При больших объемахn иm выборочные дисперсииD_в(X) иD_в(Y) являются достаточно точными оценками генеральных дисперсий, поэтому можно считать генеральные дисперсии приближенно известными.

В качестве критерия проверки нулевой гипотезы Н₀ берут случайную величину

.

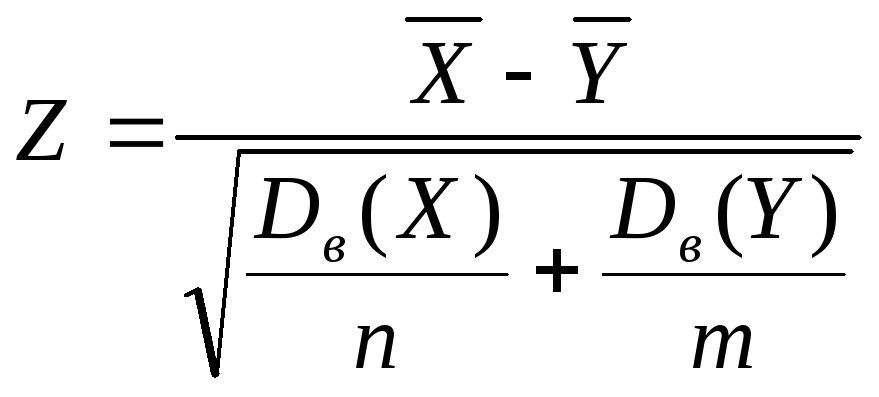Величина Zраспределена приближенно нормально с параметрамиM(Z) = 0 иσ(Z) = 1, поэтому критические точки находятся по таблице функции Лапласа Ф(x) (Приложение 3).

Построение критической области при проверке нулевой гипотезы производится по-разному в зависимости от вида противоречащей гипотезы.

1. Нулевая гипотеза Н₀ :M(X) =M(Y) , противоречащая гипотезаН₁ :M(X) ≠M(Y).

В этом случае критическая область является симметричной двусторонней и определяется неравенствами: Z < -z_кр иZ>z_кр. Критическую точкуz_кр при выбранном уровне значимости α находят из равенства Ф(z_кр) = (1- α)/2 по таблице функции Лапласа. По выборочным данным вычисляется наблюдаемое значение критерия

Z_н =.

Если | Z_н | <z_кр , то нет оснований отвергнуть нулевую гипотезу.

Если | Z_н | >z_кр , то нулевая гипотеза отвергается.

Пример 5.1. Из генеральных совокупностейX иY извлечены независимые выборки объемовn = 50 иm = 70. Выборочные средние оказались равными_в = 73 и_в = 76, а выборочные дисперсииD_в(X) = 7,5 иD_в(Y) = 8,2 . При уровне значимости α = 0,01 проверить нулевую гипотезуН₀ :M(X) =M(Y) при противоречащей гипотезеН₁ :M(X) ≠M(Y).

Решение. Наблюдаемое значение критерия равно

Z_н === - 2.36 .

Критическую точку z_кр двусторонней критической области находим из равенства

Ф(z_кр) = (1- α)/2 == 0,495 .

По таблице функции Лапласа (Приложение 3) находим, что z_кр = 2,58 . Так как оказалось, что |Z_н | <z_кр (т.е.Z_н попало в область принятия гипотезы), то нет оснований отвергнуть нулевую гипотезу.Е

2. Нулевая гипотеза Н₀ :M(X) =M(Y) , противоречащая гипотезаН₁ :M(X) >M(Y).

В этом случае критическая область является правосторонней и определяется неравенством Z>z_кр. Критическую точкуz_кр при выбранном уровне значимости α находят из равенства Ф(z_кр) = (1- 2α)/2 по таблице функции Лапласа. По выборочным данным вычисляется наблюдаемое значение критерия

Z_н =.

Если Z_н <z_кр , то нет оснований отвергнуть нулевую гипотезу.

Если Z_н >z_кр , то нулевая гипотеза отвергается.

Пример 5.2. Из генеральных совокупностейX иY извлечены независимые выборки объемовn = 40 иm = 50. Выборочные средние оказались равными_в = 28 и_в = 24, а выборочные дисперсииD_в(X) = 1,5 иD_в(Y) = 2,2 . При уровне значимости α = 0,05 проверить нулевую гипотезуН₀ :M(X) =M(Y) при противоречащей гипотезеН₁ :M(X) >M(Y).

Решение. Наблюдаемое значение критерия равно

Z_н === 14,01 .

Критическую точку z_кр правосторонней критической области находим с помощью равенства

Ф(z_кр) = (1-2α)/2 == 0,45 .

Из этого равенства по таблице функции Лапласа находим, что z_кр = 1,645. Так какZ_н >z_кр , то нулевая гипотеза отвергается.Е

3. Нулевая гипотеза Н₀ :M(X) =M(Y) , противоречащая гипотезаН₁ :M(X) <M(Y).

В этом случае критическая область является левосторонней и определяется неравенством Z< -z_кр, причемz_кр при выбранном уровне значимости α находится (как и в п.2) из равенства Ф(z_кр) = (1- 2α)/2 по таблице функции Лапласа. По выборочным данным вычисляется наблюдаемое значение критерия

Z_н =.

Если Z_н > -z_кр , то нет оснований отвергнуть нулевую гипотезу.

Если Z_н < -z_кр , то нулевая гипотеза отвергается.

Пример 5.3. Из генеральных совокупностейX иY извлечены независимые выборки объемовn = 40 иm = 50. Выборочные средние оказались равными_в = 25,7 и_в = 26, а выборочные дисперсииD_в(X) = 12,5 иD_в(Y) = 15,6 . При уровне значимости α = 0,05 проверить нулевую гипотезуН₀ :M(X) =M(Y) при противоречащей гипотезеН₁ :M(X) <M(Y).

Решение. Наблюдаемое значение критерия равно

Z_н === - 0,633 .

Значение z_кр находим также, как для правосторонней области, с помощью равенства

Ф(z_кр) = (1-2α)/2 == 0,45 .

По таблице функции Лапласа находим, что z_кр = 1,645 . Так какZ_н > -z_кр , т.е.Z_нпопало в область принятия гипотезы, то нет оснований отвергнуть нулевую гипотезуН₀ .Е

Нулевая гипотеза Н₀ :M(X) =M(Y) может быть выражена по другому. Так как выборочные средние являются несмещенными оценками генеральных средних, то естьM(X) =M() иM(Y) =M(), то нулевую гипотезу можно записать так:

Н₀ :M() =M().

Это значит, что проверка гипотезы о равенстве двух генеральных средних равносильна проверке гипотезы о равенстве математических ожиданий выборочных средних.

Выборочные средние _в и_впрактически всегда оказываются не равными друг другу. Но если окажется, что нет оснований отвергнуть нулевую гипотезуН₀ :M(X) =M(Y) о равенстве генеральных средних, то различие выборочных средних являетсянезначимым и объясняется не природой изучаемых объектов, а просто случайным отбором объектов выборки. Если же нулевая гипотеза отвергается, т.е. генеральные средние не равны друг другу, то различие выборочных средних являетсязначимым и главная причина этого есть действительное различие свойств изучаемых объектов, а неизбежная случайность отбора при составлении выборки играет второстепенную роль.