Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Инженерно-технологическая академия ЮФУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

UML_4256

.pdf

Скачиваний:

Добавлен:

01.06.2015

Размер:

6.64 Mб

Скачать

☆

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 2324 / 5024 25 26 27 28 29 30 31 32 33 34 35 36 > Следующая >>>

					1		1				2		1						3				1			1						1
= −6∫					1		1		+		2		1				−		3				1	+		1						1			dt =
= −6∫				12			t −1		+		3		t +		2		−						t +1	+	2						(t +1)2				dt =
				12			t −1				3		t +		2		4						t +1		2						(t +1)2
= −		1	ln			t −1		− 4ln				t + 2				+		9		ln		t +1		−					3			+ C .
		1																9											3
																											t		+1
		2															2
		2															2
			Осталось вместо t														подставить													x − 2			.
			Осталось вместо t														подставить																.
			Пример 4.																												x +1
			Пример 4.
					dx								x2		− x +1 = t − x																						2t2	− 2t +	2
∫					dx					=				t		2	−1								t			2	−t +1							= ∫	2t2	− 2t +	2	dt =
∫										=		x =				2					, dx =							2						dt		= ∫	t(2t −1)2			dt =
	x + x2 − x +1																							2
	x + x2 − x +1																							2
														2t −1											(2t −1)2

∫

−

dt = 2ln

2t −1

(2t −1)2

2x −1

= 2ln

x + x2 − x +1

−

+ C .

2x + 2 x2 − x +1 −1

− 32 ln 2t −1 − 32 2t1−1 + C =

2 x2 − x +1 −

Замечание.

Интеграл

∫R(x, ax2 +bx + c) dx

подстановкой

t = x +

сводится

интегралам

вида

∫R1 (t, k2

−t2 ) dt

или

∫R1 (t,

t2 ± k2 ) dt .

последним

интегралам можно

применить

тригонометрические

подстановки

t = k sinU , t = k tgU (t = k shU )

t = k secU . Интегралы

вида

∫

x2 ax2 + c

(ax2 + c)3 / 2

x ax2 + c

удобнее вычислять подстановкой x =

Пример 5. Первый способ.

∫

x = sin t

= ∫

cost dt

= ∫

1 − x2

dx = cost dt

sin t cost

sin t

= ∫

2sin

cos

2cos

2 t

231

arcsin x

= ln tg

+ C = ln tg

+ C .

Второй способ.

x =

∫

= −∫

= −ln

t + t2 −1

+ C =

1− x2

dx = −

t2 −1

= −ln

−1

+ C = ln

− ln

1+ 1− x2

+ C .

Разные на вид первообразные отличаются друг от друга на константу. Проверить самостоятельно.

в) Интегралы вида ∫ xm (a +bxn ) p dx .	(4)
Здесь m,n, p −рациональные числа, a	и b – действительные.

Подынтегральное выражение называют дифференциальным биномом. Ясно, что при целом p интеграл (4) совпадает с интегралом (1)

(можно раскрыть по биному Ньютона), рассмотренным в пункте а).

Сделаем замену x = t n . Тогда dx =

t n

−1dt и

m+1

a + bt p

m+1

−1

+ p−1

∫ xm (a + bxn ) p dx =

∫(a + bt) p t n

∫

t n

dt .

(5)

Из (5) видно, что если

m +1

или

m +1

+ p – целые числа, то этот

интеграл совпадает с общим интегралом, рассмотренным в пункте а).

Вывод.		Если хотя бы одно	из чисел p,	m +1	,	m +1	+ p	(6)
				n		n

целое,	то	подынтегральное	выражение		интеграла			(4)
рационализируется.

Чебышев доказал, что в любом другом случае интеграл (4) является неберущимся, то есть его первообразная не выражается через элементарные функции.

232

Пример 6.

m = −1 x = t3

= ∫ x−1 (1 + x1/ 3 )

−2

∫

dx =

n =1/ 3 dx = 3t2dt

3∫

x(1+ 3 x)2

t(1 +t)2

p = −2

= 3

−

dt = 3(ln

− ln

t +1

) + C =

∫

t +1 (t +1)2

t +1

3 x +1

+ C .

= 3 ln

−ln

3 x +1

m =1 Пример 7. ∫ x 1+ x3 dx = ∫ x(1+ x3 )1/ 2 dx = n = 3 .

p =1/ 2

Условия (6) не выполняются. Интеграл неберущийся.

§9. Интегрирование тригонометрических выражений. Неберущиеся интегралы

Так как не все интегралы от тригонометрических функций берутся в элементарных функциях, то рассмотрим частные случаи, когда это возможно.

а) Интегралы вида ∫R (sin x, cos x)dx.

Подынтегральное выражение рационализируется подстановкой

= t . Действительно,

x = 2arctg t

dx =

2dt

–

рациональная

1+ t2

функция аргумента t .

2sin

cos

sin x = 2sin

cos

–

рациональная

2 x

1+ t2

sin

+ cos

2 x

функция аргумента t .

2 x

cos

−sin

1−t2

cos x = cos2

−sin2

–

рациональная

2 x

1+ t2

cos

+sin

функция аргумента t .

233

1−t

dt = ∫R (t) dt –

Итак,

∫R (sin x, cos x)dx = ∫

+t2

1+t2

интеграл от рациональной функции.

Пример 1.

= t

2dt

∫

dx =

= 2∫

arctg

+C =

+ cos x

1+t2

+t2

cos x =

1−t2

1+t2

+ C .

arctg

Замечание

1. Подстановка

= t

называется

универсальной.

Однако ее применение иногда приводит к громоздким выражениям. Поэтому часто используют другие подстановки. Если подынтегральная функция R (sin x, cos x) нечетная относительно sin x, то делается замена

cos x = t , если нечетная относительно cos x , то – sin x = t . Если функция

R (sin x, cos x)

не меняет знака при одновременном изменении знака

перед sin x и cos x , то делается подстановка tg x = t .

Пример 2.

sin x = t

∫

= ∫

dt =

cos xsin

cos x dx

= dt

(1 −t

−t

1 1

1+ t

1+ sin x

= ∫

−

+ C

−

+ C .

2 1−t

2 1+ t

1−t

1−sin x

sin x

Замечание 2. Интегралы вида

∫sinαxsin β x dx, ∫cosαx cos β x dx, ∫sinαxcos β x dx вычисляются преобразованием произведения тригонометрических функций в сумму:

sinαxsin β x = 12 (cos(α − β)x − cos(α + β)x), cosαx cos β x = 12 (cos(α − β)x + cos(α + β)x),

234

sinαx cos β x = 12 (sin(α − β)x + sin(α + β)x).

Пример 3.

∫sin 3xsin 2x dx = 12 ∫(cos x − cos5x) dx = 12 sin x −101 sin 5x + C .

б) Интегралы вида ∫sinm xcosn x dx.

Если m и n – целые числа, то следует применять подстановки, о которых говорилось в замечании 1. Если m и n – рациональные числа, то подстановкой t = sin x подынтегральное выражение сводится к дифференциальному биному. Действительно,

t = sin x, dt = cos x dx, cos x =	1−sin2 t = 1−t2 . В результате получим
n−1
∫sinm xcosn x dx = ∫tm (1−t2 ) 2	dt (см. (4) §8)	(1)
Вспоминая критерий	интегрируемости	дифференциального

бинома Чебышева, найдем, что интеграл (1) берется в элементарных функциях в следующих случаях:

а)

n −1

– число целое, то есть если n – целое нечетное число;

б)

m +1

– число целое, то есть m – целое нечетное число;

в)

m +1

n −1

m + n

– число целое, то есть сумма (m + n)

–

целое четное число.

Пример 4. ∫ 3 sin xcos xdx = ∫sin3 xcos3 x dx , так как m = n =

и не

выполняется ни один из случаев а) – в), то данный интеграл не берется в элементарных функциях.

в) Интегралы вида ∫R(eα x )dx.

Подынтегральное выражение рационализируется подстановкой t = eα x . Действительно,

dt =αeα x dx dx = αdteα x . ∫R(eα x ) dx = α1 ∫R(t) dtt – интеграл от рациональной функции.

235

Пример 5.

∫

ex = t

= ∫

= 2∫

+ ch x

tdx = dt

(t + 2)2

−3

t +

t + 2

−

+C =

ex + 2

−

+ C .

3 t + 2

3 ex + 2

Если

мы

дифференцировали

комплексную

функцию

действительного аргумента (см. §11 гл. 6), то очевидно ее можно и проинтегрировать. Если параметр α в интеграле ∫R(eα x )dx чисто

мнимый, то данный интеграл будет интегралом от тригонометрического выражения.

Пример 6.

eix = t

∫

itdx = dt

= −i∫

= −2i∫

+ cos x

2 +

t2 + 4t +1

cos x =

(t +t

−1

)

t +

= −2i∫

= −

t + 2 − 3

= −

eix + 2 − 3

+ C

(t +

2)2

−3

3 t + 2 +

3 eix + 2 +

= −

1+ 2cos x + i

3 sin x

+ C = −

eiϕ

+ C =

+ C

(2 + 3 )(2 + cos x)

2 +

arctg

3 sin x

+C .

1+ 2cos x

Хотя ответ по форме записи не совпадает с ответом примера 1, но он верный. Убедитесь в этом самостоятельно дифференцированием.

Мы уже знаем, что интеграл дифференциального бинома не всегда выражается через элементарные функции. Такие интегралы называют неберущимися интегралами.

Существует множество неберущихся интегралов, определяющих неэлементарные функции, которые часто используются как в теоретических, так и прикладных вопросах математики. Приведем

некоторые из них. ∫ sinx x dx одна из первообразных этого интеграла называется интегральным синусом и обозначается si(x) .

236

∫	dx	−интегральный логарифм (li x) .	∫	dϕ	– эллиптический
	ln x			1− k 2 sin2 ϕ

интеграл первого рода. ∫e−x2 dx – интеграл вероятности. Для этих функций составлены специальные таблицы.

237

ГЛАВА 8. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ

§1. Понятия интегралов Римана и Стилтьеса. Суммы Дарбу

Напомним (см. §12 гл. 6) определение разбиения отрезка [a,b] –

это	любое конечное множество			точек τ ={x	}n	отрезка	таких,	что
a = x0 < x1 < x2 < ... < xn = b .				i	∞
a = x0 < x1 < x2 < ... < xn = b .
	Каждый из отрезков [xi−1, xi ]			называется отрезком разбиения τ , а
его	длина	обозначается	∆xi = xi − xi−1, i =1,2,..., n.				Величину
δτ = max ∆xi		называют диаметром разбиения				τ . Разбиение		τ′
	i

называется измельчением разбиения τ , если τ′ τ , то есть всякая точка разбиения τ является точкой разбиения τ′.

Пусть	f (x) – ограниченная на отрезке			[a,b]		и заданная в каждой
точке этого	отрезка функция, а	τ ={x }n			–	некоторое	разбиение
		i	i=0
отрезка [a,b]. Пусть Mi = sup f (x), mi = inf			f (x) . Составим суммы
	∆xi	∆xi
	n				n
	S (τ, f )= ∑Mi ∆xi , s(τ,			f )= ∑mi ∆xi			(1)
	i=1				i=1
и рассмотрим величины			−
	n		−
	inf S(τ, f ) = inf (∑Mi ∆xi ) = ∫ f (x) dx,
	i=1						(2)
	n						(2)
	n
	sup s(τ, f ) = sup(∑mi ∆xi ) = ∫ f (x) dx.
	i=1		−

Верхние и нижние грани в (2) берутся по всем возможным разбиениям отрезка [a,b].

Суммы (1) называют верхней и нижней суммами Дарбу, а выражения (2) – верхним и нижним интегралами Римана функции f (x) по отрезку [a,b].

−	= ∫ f (x) dx , то функцию f (x)
Определение 1. Если ∫ f (x) dx	= ∫ f (x) dx , то функцию f (x)
	−

называют интегрируемой по Риману на отрезке [a,b], а общее значение

238

верхнего и нижнего интегралов Римана называют интегралом Римана

	b
функции f (x) на отрезке [a,b] и обозначают ∫ f (x) dx.
Пишут также f (x) R , где R –	a
Пишут также f (x) R , где R –	множество всех	функций,
интегрируемых по Риману на отрезке [a,b].
Так как функция f (x) ограничена,	а ограниченное	множество

всегда имеет точную верхнюю и нижнюю грани, то верхние и нижние интегралы Римана существуют для любой ограниченной функции. Остается только выяснить условия, при которых они совпадают.

Пусть α(x) − монотонно возрастающая функция на				[a,b].
Очевидно, она ограничена на		[a,b]. Если τ ={xi }in=0 – некоторое
разбиение [a,b], то ∆αi =α(xi ) −α(xi−1 ) > 0. Для любой ограниченной
на [a,b] функции f (x) составим суммы:
	n	n	∆αi .
S =	(τ, f ,α) = ∑Mi ∆αi , s(τ, f ,α) = ∑mi		∆αi .	(3)
Здесь Mi и mi	i=1	i=1
Здесь Mi и mi	– те же, что и в (1).
Рассмотрим выражения:
−		n
∫ f (x) dα = inf S		= inf (∑Mi ∆αi ),
		i=1		(4)
		n		(4)
		n
∫ f (x) dα =sup s = sup(∑mi ∆αi ).
−		i=1

Здесь верхние и нижние грани берутся также по всем разбиениям.

−

Определение 2. Если ∫ f (x) dα = ∫ f (x) dα , то их общее значение

−

называют интегралом Стилтьеса от функции f (x) относительно

функции α(x) на отрезке [a,b]. Обозначают ∫ f (x) dα .

Замечание 1. При α(x) = x интеграл Стилтьеса совпадает с

интегралом Римана, следовательно, интеграл Римана – частный случай интеграла Стилтьеса.

Замечание 2. Значения mi , Mi , ∆xi , ∆αi не зависят от обозначения

переменной. Поэтому интегралы Римана и Стилтьеса не зависят от обозначения переменной интегрирования, то есть

239

b	b	b	b	(y).
∫ f (x) dx = ∫ f ( y) dy, ∫ f (x) dα (x)= ∫ f ( y) dα				(y).
a	a	a	a
Теорема 1. Если τ – измельчение разбиения τ , то
s(τ , f ,α) ≥ s(τ, f ,α), S(τ , f ,α) ≤ S(τ, f ,α) .				(5)

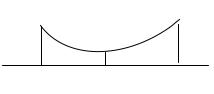
f(x)

xi-1

Доказательство. Допустим сначала, что τ содержит только на одну точку больше, чем τ (см. рис.).

Обозначим эту точку x .

Пусть µ

= inf f (x),

x x

, x

, µ

= inf

f (x),

x , x

i−1

Очевидно, µ1 ≥ mi и µ2 ≥ mi .

(6)

Найдем разность s(τ , f ,α) − s(τ, f ,α) =

= µ1 (α(x ) −α(xi−1 ))+ µ2 (α(xi ) −α(x ))− mi (α(xi ) −α(xi−1 ))=

= (µ − m )(−α(x

))+ (µ

− m )

α(x ) + (µ − m + m − µ

) α(x ) =

1 i

i−1

= (µ1 − mi ) (α(x ) −α(xi−1 ))+(µ2 − mi ) (α(xi ) −α(x ))≥ 0

(см. (2)), то

есть s(τ , f ,α) ≥ s(τ, f ,α)

и первое из неравенств (5) доказано.

Если τ

содержит

на

точек больше, чем τ , то повторив

проведенные рассуждения k

раз, мы докажем первое из неравенств (5)

в общем случае. Второе неравенство в (5) доказывается аналогично. Теорема доказана.

Таким образом, с измельчением разбиения нижние суммы могут только возрасти, а верхние – только уменьшиться.

Разбиение τ называется общим измельчением разбиений τ1 и τ2 ,

если τ =τ1 τ2 .
Следствие.	При любых разбиениях нижняя сумма Дарбу-
Стилтьеса не более верхней, то есть
	s(τ1, f ,α) ≤ S(τ2 , f ,α).	(7)
	240

<<< < Предыдущая 12 13 14 15 16 17 18 19 20 21 22 2324 / 5024 25 26 27 28 29 30 31 32 33 34 35 36 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20191.07 Mб17Uchebnoe_posobie_ch1.doc
#
05.09.2019687.71 Кб13Uchebnoe_posobie_metrologia.docx
#
01.06.20152.46 Mб17UMK_po_Menedzhmentu_modul_2.pdf
#
01.06.2015359.44 Кб7umk_treb.pdf
#
01.06.2015903.17 Кб14UML_1321.pdf
#
01.06.20156.64 Mб21UML_4256.pdf
#
01.06.2015321.05 Кб16UML_4497.pdf
#
01.06.20151.11 Mб7UML_4562.pdf
#
01.06.2015641 Кб9UML_4564.pdf
#
01.06.2015943.33 Кб7UML_4597.pdf
#
01.06.20151.72 Mб68UML_4797.pdf