
- •Содержание
- •1. ОБЩИЕ РЕКОМЕНДАЦИИ СТУДЕНТУ-ЗАОЧНИКУ ПО РАБОТЕ НАД КУРСОМ ВЫСШЕЙ МАТЕМАТИКИ
- •2. ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ
- •3. ПРОГРАММА
- •3.1. Элементы линейной алгебры и аналитической геометрии
- •3.2. Введение в математический анализ
- •3.3. Дифференциальное исчисление функций одной переменной
- •3.4. Применение дифференциального исчисления для исследования функций и построения их графиков
- •4. ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
- •4.1. Матрицы
- •4.3. Скалярное произведение векторов
- •4.4. Векторное произведение векторов
- •4.5. Смешанное произведение векторов
- •4.6. Прямая и плоскость
- •4.7. Линии второго порядка
- •4.8. Поверхности второго порядка
- •5. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •5.1. Предел числовой последовательности. Предел функции
- •6. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
- •6.1. Дифференцирование функций
- •6.2. Производные и дифференциалы высших порядков. Дифференцирование функций, заданных параметрически
- •6.3. Приложение теорем Ролля, Лагранжа, Коши. Правило Лопиталя
- •6.4. Формула Тейлора и ее приложения
- •7.1. Исследование функций на экстремум. Выпуклость и вогнутость кривой, точки перегиба. Асимптоты
- •7.2. Исследование функций и построение их графиков
- •КОНТРОЛЬНАЯ РАБОТА № 1
- •Литература

П р и м е р 5.4. Установить вид точек разрыва функции
1
f(x) = e x+1.
Ре ш е н и е . Данная функция непрерывна всюду, кроме точки
х= –1, в которой f(x) не определена.
Поскольку
|
f (x) = |
|
1 |
= 0 (т.к. |
1 |
|
→ −∞ при x → −1 − 0 ), |
||||
lim |
lim |
|
e |
x+1 |
|
||||||
x + 1 |
|||||||||||
x→−1−0 |
|
x→−1−0 |
|
||||||||
lim f (x) = |
|
1 |
= +∞ (т.к. |
1 |
|
→ +∞ при x → −1 + 0 ), |
|||||
|
e |
|
|
||||||||
lim |
x+1 |
|
|||||||||
x + 1 |
|||||||||||
x→−1+0 |
x→−1+0 |
|
|
|
|
|
|
||||
т.е. правосторонний предел бесконечен, то х = –1 – точка разрыва второго рода.
6. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
6.1. Дифференцирование функций
Производной функции y = f(x) в точке х называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
f '(x) = lim |
y , |
x→0 |
x |
где y = f (x + x) − f (x). |
|
Производная обозначается у', y'(x), y'x, dy . dx
Правила дифференцирования функций. Пусть С – постоянная,
аu(x) и v(x) – дифференцируемые функции. Тогда
1)C' = 0,
45

2)(Cu)'= Cu',
3)(u ± v)'= u'±v',
4)(u ×v)'= u'v + v'u ,
u ' |
u'v - uv' |
|
||||
5) |
|
|
= |
|
|
(v ¹ 0) . |
|
v2 |
|||||
v |
|
|
||||
Производная сложной функции y = f(u(x)). Если функция u = u(x)
дифференцируема в точке х, а функция y = f(u) дифференцируема в соответствующей точке u = u(x), то сложная функция y = f(u(x)) дифференцируема в точке х и ее производная равна
y'(x) = f 'u (u) × u'(x).
Таблица производных.
1. (uα )'= auα−1 ×u', a ¹ 0; 2. (au )'= au ×ln a ×u';
3. (eu )'= eu × u';
4. |
(loga u)'= |
|
|
1 |
|
|
|
×u'; |
|
|
|
||||||
u |
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
×ln a |
|
|
|
|
|
||||||||
5. |
(ln u)'= |
×u'; |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|||
6. |
(sin u)'= cosu × u'; |
|
|
|
|||||||||||||
7. |
(cosu)'= -sin u × u'; |
|
|
|
|||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
8. ( tg u)'= |
|
|
|
|
×u'; |
|
|
|
|||||||||
cos2 u |
|
|
|
|
|||||||||||||
9. |
(ctg u)'= - |
|
1 |
|
|
×u'; |
|
|
|
||||||||
|
|
|
|
|
|
|
|||||||||||
sin2 u |
|
|
|
||||||||||||||
10. (arcsinu)'= |
|
1 |
|
×u'; (arccosu)'= - |
1 |
×u'; |
|||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1- u2 |
1- u2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
46 |
|
|
|
|
11. (arctg u)'= |
|
1 |
×u'; (arcctg u)'= - |
1 |
×u'; |
|
+ u2 |
1+ u 2 |
|||
1 |
|
|
|||
12.(sh u)'= ch u × u';
13.(ch u)'= sh u × u';
14. (th u)'= |
1 |
×u'; |
(cth u)'= - |
1 |
×u'. |
|
ch2 u |
|
|
||||
|
|
|
sh2 u |
|
||
Функция |
y = f (x), |
x Î (a; b), неявно задана |
уравнением |
|||
F (x, y) = 0, |
если |
для |
всех x Î (a; b) выполняется |
равенство |
||
F (x, f (x)) = 0.
Для вычисления производной функции, заданной неявно, следует тождество F (x, f (x)) = 0 продифференцировать по х (рассмат-
ривая левую часть как сложную функцию от х), а затем полученное уравнение решить относительно f'(x).
П р и м е р 6.1. Найти производную показательно-степенной функции
|
|
1 |
2x |
y = 1 |
+ |
|
. |
|
|||
|
|
x |
|
Р е ш е н и е . Логарифмируя, а затем дифференцируя левую и |
|||
правую части равенства, получим |
|
|
|
|
|
1 |
|
ln y = 2x ln 1 |
+ |
|
; |
|
|||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y¢ |
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|||
|
= 2 ln 1 |
+ |
|
|
+ x |
|
|
|
|
- |
|
|
. |
|
y |
|
|
|
1 |
x2 |
|||||||||
|
|
|
x |
|
1 + |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Умножая обе части равенства на у, имеем:
47

|
|
1 2x |
|
|
|
1 |
|
1 |
|
||
y¢ = 2 1 |
+ |
|
|
× ln 1 |
+ |
|
|
- |
|
. |
|
|
|
|
|||||||||
|
|
x |
|
|
|
x |
|
|
|
||
|
|
|
|
x +1 |
|||||||
П р и м е р 6.2. Найти производную функции y = f (x) , задан-
ной неявно уравнением x2 - 2x2 y2 + 5x + y - 5 = 0 .
Ре ш е н и е . Дифференцируя по х тождество x2 - 2x2 y2(x) +5x +
+y(x) - 5 = 0 , получим 2x - 4xy2 - 4x2 yy¢ + 5 + y¢ = 0 . Выражая y′ из этого равенства, находим:
y¢ = 4xy2 - 2x - 5 .
1 - 4x2 y
Дифференциал dy функции y = f (x) равен произведению ее производной на приращение x независимой переменной: dy = f ′(x) x
или dy = f ′(x)dx .
При достаточно малых x имеет место приближенная формула y ≈ dy , т.е. f (x + x) − f (x) ≈ f ′(x) x или f (x + x) ≈ f (x) + f ′(x) x .
П р и м е р 6.3. Найти приближенное значение объема шара, радиус которого равен 1,02 м.
Р е ш е н и е . Воспользуемся формулой V = V (r) = 4 πr3 . Тогда
3
V¢ = 4pr2 . Полагая r =1, r = 0,02, получим V(1,02) ≈V(1) +V′(1)0,02=
=4 π + 4π0,02 ≈ 4,43 м3. 3
6.2.Производные и дифференциалы высших порядков. Дифференцирование функций, заданных параметрически
Производной второго порядка функции y = f (x) называется
48
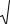
производная от ее производной y′ = f ′(x) , т.е. y′′ = |
d 2 y |
= ( y′)′ . |
|
dx2 |
|||
|
|
Аналогично определяются производные более высоких порядков y′′′ = ( y′′)′,K, y(n) = ( y(n−1) )′ .
Дифференциалы высших порядков функции y = f (x) (x – независимая переменная) вычисляются по формулам
d 2 y = y′′(dx)2 ,K, d n y = y(n) (dx)n .
Если функция y = y(x) |
|
задана параметрически соотношениями |
|||||||||||||||||||
x = x(t), |
y = y(t) , причем |
|
|
′ |
|
|
то ее первая |
′ |
и вторая |
′′ |
|||||||||||
|
x (t) ¹ 0 , |
yx |
yxx |
||||||||||||||||||
производные находятся по формулам: |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
y′ |
|
′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
y′ |
|
|
|
|
|
|
( y′ )′ |
x′ |
|
y′′ x′ − x′′ y′ |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y′ |
= |
t |
, y′′ |
= ( y′ )′ |
|
= |
x t |
= |
t |
t |
= |
|
tt t |
tt t |
. |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
x |
|
xt′ |
|
xx |
x |
x |
|
xt′ |
|
xt′ |
|
|
|
(xt′)3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
П р и м е р |
6.4. Найти выражение для производной n-го порядка |
||||||||||||||||||||
функции y = |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р е ш е н и е . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y′ = − |
1 |
; |
y′′ = |
2 |
; |
y′′′ = − |
2 × 3 |
= − |
3! |
,K, y(n) = (−1)n |
n! |
. |
|||||
|
|
|
|
|
|
||||||||||||
|
x2 |
|
x3 |
4 |
|
x4 |
|
|
|
xn+1 |
|||||||
|
|
|
x |
|
|
|
|||||||||||
П р и м е р |
6.5. Найти производную 2-го порядка от функции |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
|
|
||
y = y(x) , заданной неявно уравнением |
|
x2 + y2 = e |
|
x . |
|||||||||||||
Р е ш е н и е . По правилу дифференцирования функции, заданной неявно, получаем:
49
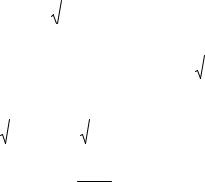
|
|
|
|
|
|
|
|
|
arctg |
y |
|
|
|
|
|
||||
|
|
|
|
x + yy′ |
x ( y′x − y) |
||||||||||||||
|
|
|
|
= |
e |
|
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x2 + y2 |
|
|
|
x2 + y2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
arctg |
y |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Отсюда, используя равенство e |
x = x2 + y2 , имеем: |
||||||||||||||||||
|
|
||||||||||||||||||
|
x + yy′ |
|
= |
|
y′x − y |
или x + yy′ = y′x − y . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x2 + y2 |
x2 + y2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Следовательно, y′ = x + y . x − y
Дифференцируя последнее равенство и используя найденное для y′ выражение, получим:
y′′ = |
(1 + y′)(x − y) − (1 − y′)(x + y) |
= |
|
x − y + xy′ − yy′ − x − y + xy′ |
+ |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
(x − y)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x − y)2 |
|
|
|
|||||||||||
|
|
yy′ |
|
|
|
2xy′ − |
|
|
|
|
2(x |
x + y |
|
− y) |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
+ |
= |
2y |
= |
|
|
|
|
x − y |
|
|
= |
2(x2 + y |
2 ) |
. |
|
||||||||||||||||||||||
(x − y)2 |
|
|
|
|
|
|
|
|
(x − y)2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
(x − y)2 |
|
|
|
|
|
|
|
|
(x − y)3 |
|
|||||||||||||||||||||||
П р и м е р 6.6. Найти производную 2-го порядка функции, |
за- |
||||||||||||||||||||||||||||||||||||
данной параметрически: y = ln t, |
x = t 2 , t (0;+∞). |
|
|
|
|||||||||||||||||||||||||||||||||
Р е ш е н и е . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
y′ = |
1 |
, x′ = 2t, y′ |
= |
yt′ |
|
= |
1 |
, |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
xt′ |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
t |
|
|
t |
t |
|
|
|
|
|
|
x |
|
|
|
|
|
|
2t 2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
′ ′ |
|
|
|
2 |
|
− 13 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
y′′ |
|
|
( yx )t |
|
2t |
|
t |
|
|
|
|
|
|
|
= − |
1 |
. |
|
|
|
|||||||||||||||
|
|
|
= |
= |
|
= |
|
|
|
|
t |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
xx |
|
|
|
xt′ |
|
|
|
|
2t |
|
|
|
|
|
|
|
2t |
|
|
|
|
|
2t 4 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
