4. Повторение испытаний

4.1. Формула Бернулли

Если в каждом из n независимых испытаний вероятность появления события А постоянна и равна p, то вероятность того, что в n испытаниях событие А произойдет ровно m раз, определяется по формуле Бернулли . (11)

4.2. Формула Пуассона

Если n велико, а p мало ( обычно p<0,1; npq9 ), то вместо формулы Бернулли применяют приближенную формулу Пуассона , (12) где=np.

4.3. Локальная теорема Лапласа

Если n велико, вероятность может быть вычислена по приближенной формуле, (13) где. Значения функции(x) определяются из таблицы .

Вероятность того, что вn независимых испытаниях, в каждом из которых вероятность появления события А равна p(0<p<1), событие А наступит не менее раз и не болеераз, приближенно равна, (14) где - функция Лапласа,,. Значенияопределяются из таблицы;=1/2 при x>5,= –.

Пример 14. В мастерской имеется 10 моторов. При существующем режиме работы вероятность того, что в данный момент не менее 8 моторов работают с полной нагрузкой, равна 0,8. Найти вероятность того, что в данный момент не менее 8 моторов работают с полной нагрузкой.

Решение. Рассмотрим события: А={не менее 8 моторов из 10 в данный момент работают с полной нагрузкой}; B, C, D - события, состоящие в том, что работают соответственно 8, 9 и 10 моторов. Тогда A=B+C+D. Так как события B, C и D несовместны, P(A)=P(B)+P(C)+P(D). Найдем вероятности событий B, C и D по формуле Бернулли (11): 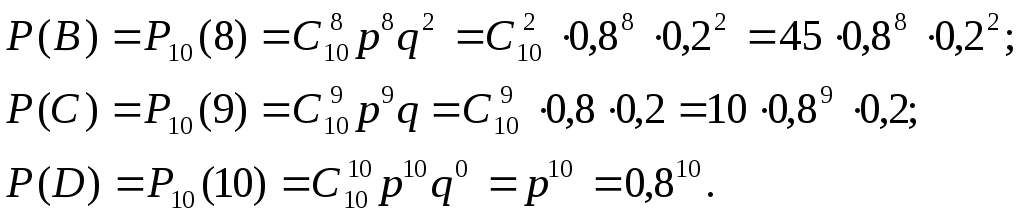Тогда.

Пример 15. Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.

Решение. По условию n=100, m=75, p=0,8, q=0,2. Так как n=100 велико, воспользуемся формулой (13) локальной теоремы Лапласа. Для этого найдем . По таблице найдем(–1,25)=0,1826. Искомая вероятность .

Пример 16. Предприятие отправило на базу 5000 изделий. Вероятность того, что в пути изделие повредится, равна 0,0002.Найти вероятность того, что на базу прибудет ровно 3; не более 3 негодных изделий.

Решение. Воспользуемся формулой Пуассона (12). В данном случае m=3, p=0,0002, n=5000, =np=1; . Вероятность того, что на базу прибудет не более 3 негодных изделий, равна

Пример 17. Имеется 100 станков одинаковой мощности, работающих независимо друг от друга, в одинаковом режиме, при включенном приводе, в течение 0,8 всего рабочего времени. Какова вероятность того, что в произвольно взятый момент времени окажутся включенными от 70 до 86 станков?

Решение. Воспользуемся интегральной теоремой Лапласа ( формула (14)) , где- функция Лапласа;;.

Искомая вероятность .

4.5. Наивероятнейшее число появлений события

Наивероятнейшее число появления события А в n независимых испытаниях, в каждом из которых оно может появиться с вероятностью p ( и не появиться с вероятностью q = 1 – p ), определяется из двойного неравенства np-qnp+p, (15) а вероятность появления события А хотя бы один раз вычисляется по формуле P=1 – qⁿ. (16)

Пример 18. Оптовая база снабжает 10 магазинов, от каждого из которых может поступить заявка на очередной день с вероятностью 0,4, независимо от заявок других магазинов. Найти наивероятнейшее число заявок в день и вероятность получения этого числа заявок.

Решение. Запишем двойное неравенство (15) при n=10, p=0,4, q=0,6 для этого случая: 100,4-0,6100,4+0,4 или 3,44,4.

Так как число должно быть целым, положительным, то=4. Найдем вероятность получения этого числа по формуле Бернулли (11).

Пример 19. Вероятность попадания в десятку при одном выстреле равна 0,3. Сколько должно быть произведено независимых выстрелов, чтобы вероятность хотя бы одного попадания в десятку была больше 0,9?

Решение. Для решения этой задачи воспользуемся формулой (16). В данном случае p=0,3; q=0,7; P>0,9; число выстрелов n необходимо определить из неравенства 1-(0,7)ⁿ>0,9. Решим его: (0,7)ⁿ<0,1, отсюда , т.е. n7.