3.3. Расход элементарной струйки и расход через поверхность

Расходом называется количество жидкости, протекающее через живое сечение потока (струйки) в единицу времени. Под живым сечением, или просто сечением потока, понимают в общем случае поверхность в пределах потока, проведенную нормально к линиям тока.

Это количество можно измерить в единицах объема, в весовых единицах или в единицах массы, в связи с чем различают объемный Q, весовой и массовый расходы. Для элементарной струйки, имеющей бесконечно малые площади сечений, можно считать истинную скорость V одинаковой во всех точках каждого сечения. Следовательно, для этой струйки объемный (), весовой () и массовый () расходы будут равны

(3.14)

где dS - площадь сечения струйки.

Основываясь на законе сохранения вещества, на предположении о сплошности (неразрывности) течения и на указанном выше свойстве трубки тока, заключающемся в ее «непроницаемости», для установившегося течения несжимаемой жидкости можно утверждать, что объемный расход во всех сечениях элементарной струйки один и тот же

(вдоль струйки). (3.15)

Это уравнение называется уравнением объемного расхода для элементарной струйки.

В векторном анализе потоком любого вектора а называется интеграл по некоторой поверхности от проекции вектораа на нормаль n в каждой точке поверхности, т.е.

. (3.16)

Соответственно с этим поток вектора скорости определяется величиной, равной

. (3.17)

Поток вектора скорости физически представляет собой объемный расход некоторой жидкости (среды) через поверхность .

Если поверхность замкнутая, то при отсутствии внутри поверхности источников и стоков поток вектора скорости через замкнутую поверхность будет равен нулю

. (3.18)

Для потока конечных размеров скорость имеет различное значение в разных точках сечения, поэтому расход надо определять как сумму элементарных расходов струек, т.е.

. (3.19)

Обычно в рассмотрение вводят среднюю по сечению скорость , откуда получаем

(вдоль потока). (3.20)

Для потока конечных размеров, ограниченного непроницаемыми стенками, будем иметь

(вдоль потока). (3.21)

Уравнение расхода является следствием общего закона сохранения вещества для частных условий, в частности для условий сплошности (неразрывности) течения.

При наличии источника поток вектора скорости будет составлять

, (3.22)

а при наличии стока

. (3.23)

3.4. Уравнение неразрывности (сплошности)

В механике обычно рассматриваются законы сохранения четырех величин: массы, количества движения, момента количества движения и энергии. Все законы сохранения относятся к так называемым изолированным системам. Будем в дальнейшем называть систему изолированной или замкнутой в том случае, если через контрольную поверхность - окружающую систему - нет переноса массы, количества движения и энергии. На изолированную систему не действуют внешние силы.

Закон сохранения массы для изолированной системы выражается в том, что масса m такой системы остается постоянной во все время движения, т.е. количество вещества остается постоянным или

. (3.24)

Общий закон сохранения массы применительно к сплошным средам получает свое выражение в уравнении неразрывности или сплошности движения. Для получения этого уравнения при отсутствии источников или стоков массы применим закон сохранения массы к некоторому элементарному объему , движущемуся вместе со средой, имеющей плотность . Так как

(3.25)

то , (3.26)

или . (3.27)

Относительное изменение объема в данной точке за единицу времени равно дивергенции вектора скорости в данной точке, т.е.

. (3.28)

Тогда уравнение неразрывности движения примет вид

. (3.29)

Если плотность зависит и от времени и от координат, т.е. , то

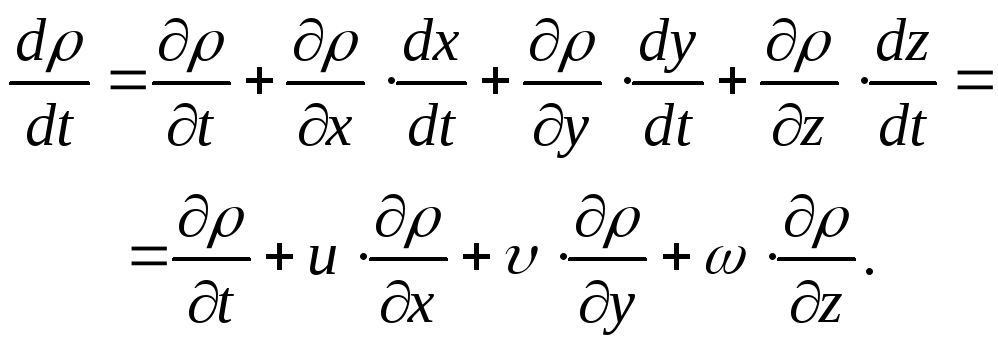(3.30)

Подставив это выражение в (3.29), получим другой вид уравнения неразрывности (в проекциях на прямоугольные оси)

(3.31)

или

. (3.32)

Последние слагаемые составляют дивергенцию , поэтому уравнение (3.32) в дифференциальной форме имеет вид

. (3.33)

Для стационарного движения, при котором , уравнение неразрывности примет вид

. (3.34)

При наиболее простом случае движения, когда плотность жидкости постоянна и не зависит от координат и времени, т.е. , уравнение неразрывности будет иметь вид

. (3.35)

Уравнение неразрывности (сплошности) также может быть представлено в интегральной форме в виде

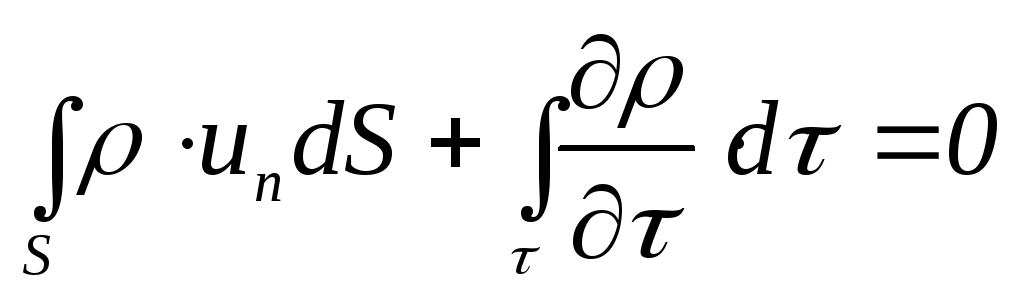, (3.36)

где S - поверхность, ограничивающая объем .