§19. Бесконечно малые и бесконечно большие функции

Пусть f(x) определена в некоторой проколотой окрестности точки:

Определение 1.Функцияf(x) называетсябесконечно малойв точке а (при ), если.

По определению это значит, что выполняется.

Определение 2.Функцияf(x) называетсябесконечно большой в точке а (при ), есливыполняется.

Обозначается .

Определение 3.Функцияf(x) называетсяположительной бесконечно большой функцией при , есливыполняется, обозначается.

Определение 4.Функцияf(x) называетсяотрицательной бесконечно большой функцией при , есливыполняется, обозначается.

Пример 1.Доказать, что- бесконечно малая функция при, то есть.

 Выберем . Надо найти::выполняетсянадо взять.

Пример 2.Доказать, что- бесконечно большая функция при,.

 Выберем . Найдем::выполняетсянадо взять.

Пример 3.Доказать, что.

 Выберем . Найдем::выполняется.

Теорема 1.1) Сумма, разность и произведение двух бесконечно малых функций в точкеаявляется бесконечно малой функцией в точкеа.

2) Произведение бесконечно малой функции в точке ана ограниченную в окрестности точкиафункцию является бесконечно малой функцией в точкеа.

Доказательство.

1) Пустьf(x),g(x) - бесконечно малые в точкеафункции. Докажем, чтоf(x)+g(x) - бесконечно малая функция в точкеа. Выберем. По определению:выполняется,

выполняется.

Возьмём выполняется.

Разность и произведение – аналогично: ,

(можно взять не, а).

2) Пусть f(x) – ограничена в окрестности точкиа, аg(x) - бесконечно малая функция в точкеа.

Тогда по определению существует выполняется;

выполняется.

Возьмём выполняется.

Теорема 2.

1) Пусть f(x) - бесконечно большая функция при. Тогда- является бесконечно малой функцией при;

2) Пусть f(x) - бесконечно малая функция прии. Тогда- бесконечно большая функция при.

Доказательство.

1) Пусть. Выбереми положим.

 для выбранноговыполняется(так как, то естьв, тоимеет смысл).

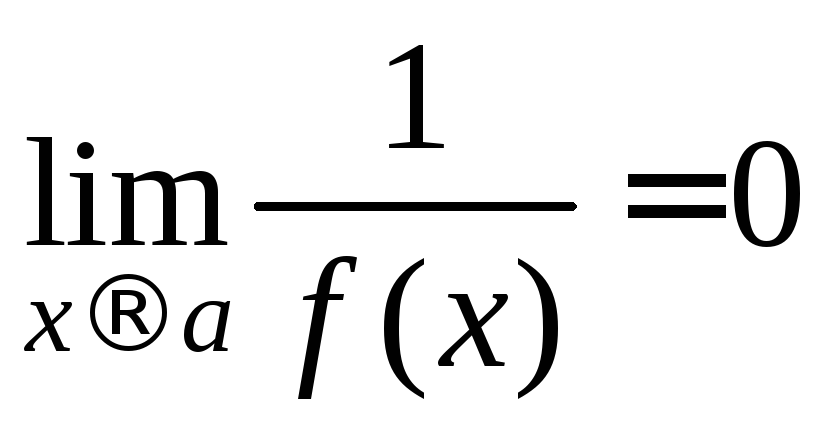2) аналогично.

Следствие 1.Произведение постоянной С на бесконечно малую функцию приесть бесконечно малая функция при.

Следствие 2.Произведение любого конечного числа бесконечно малых функций приесть бесконечно малая функция при.

Следствие 3.Произведение функцииf, имеющей предел прина бесконечно малую функцию приесть бесконечно малая функция при, то есть если существует,.

Общее понятие предела функции.

Понятие предела можно обобщить на случаи:а=а-0, а=а+0, а=. Всего 4 варианта для элементаА, и 6 вариантов дляа.Итого 24 определения предела функции.

Общее определение.выполняется.

Пример., то естьвыполняется.

Бесконечные пределы и неопределенности

(дополнения к теореме 8 §6)

1. ,

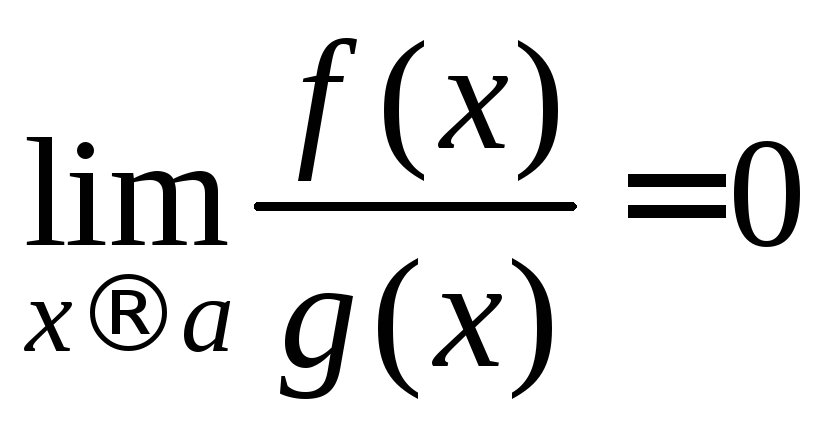
2. ,

3. ,

4. ,

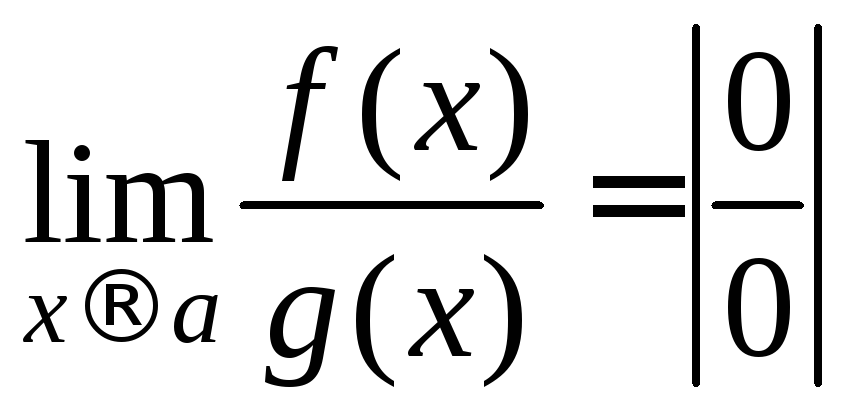
5. ,

6. ,

7. ,

8. ,

9. ,

10. ,

11. ,

§20. Сравнение бесконечно малых функций и бесконечно больших функций

Пусть все рассмотренные функции определены в , где,,,. Пустьи- бесконечно малые функции при. Сравним эти функции по быстроте их стремления к нулю. Для этого составим отношение(в).

Определение 1.Если, тоназываетсябесконечно малой высшего порядкапо отношению к бесконечно малойпри.

Обозначается: ,(– омикрон, греческая буква).

Говорят, что бесконечно мала по сравнению спри.

Пример 1. ,, при,.

.

Следовательно, при.

Определение 2.Если, тоестьбесконечно малая функция низшего порядка, чемпри.

Определение 3.Если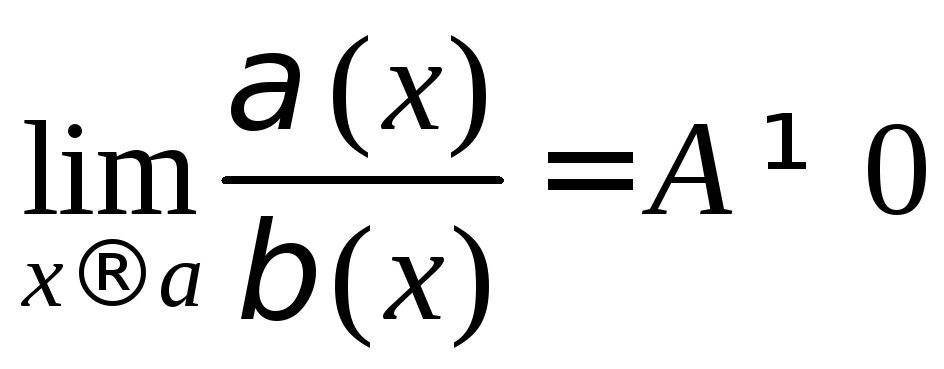, тоибесконечно малые одного порядка при .

Пример 2. 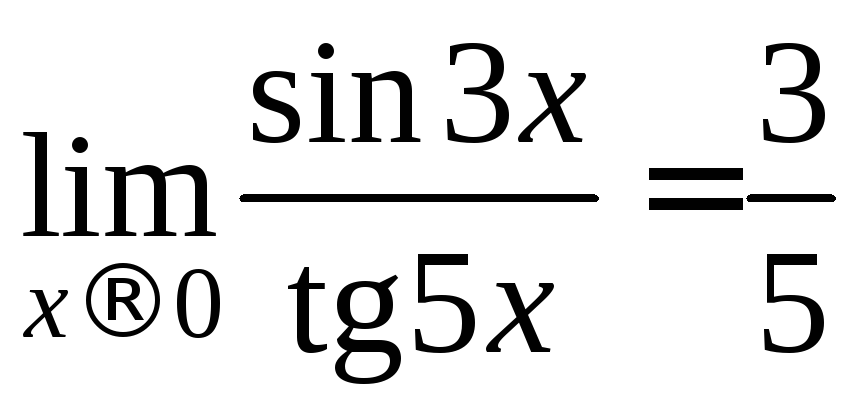(см. раньше)и- бесконечно малые одного и того же порядка при.

Определение 4.Если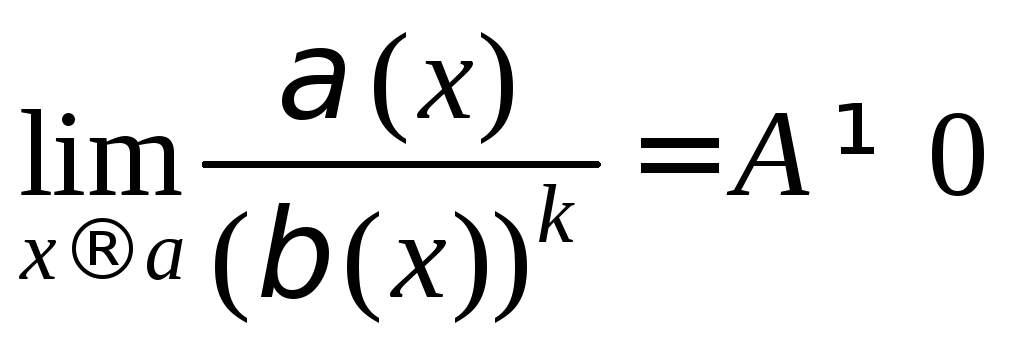,, тоявляетсябесконечно малой k-го порядкапо сравнению спри.

Пример 3. ,.

.

Значит, - бесконечно малая функция 4–го порядка по сравнению спри.

Теорема 1.Произведение двух бесконечно малых функций приесть бесконечно малая функция привысшего порядка, чем каждая из них, то есть если,-бесконечно малая функция, то

.

Доказательство.

при;

при.

Эквивалентные бесконечно малые функции

Определение 5.Если, тоиназываютсяэквивалентными бесконечно малыми функциями при .

Обозначается: ~,.

Примеры. Прих0sinxx

tgx x

ln(1+x)x(докажем позже)

e^x -1  x (докажем позже)

arcsinx  x

arctgx  x

(1+x)^kkx, (докажем позже)

Теорема 2.Для того, чтобы(x) и(x) были эквивалентными бесконечно малыми принеобходимо и достаточно, чтобы их разность была бесконечно малой функцией более высокого порядка, чем(x) и(x).

То есть (x) ~(x),.

Доказательство.

,, т. к.по т.1.

Теорема 3.Если при(х) ~ ₁(х) , (х) ~ ₁(х) и существует, то существует, то есть.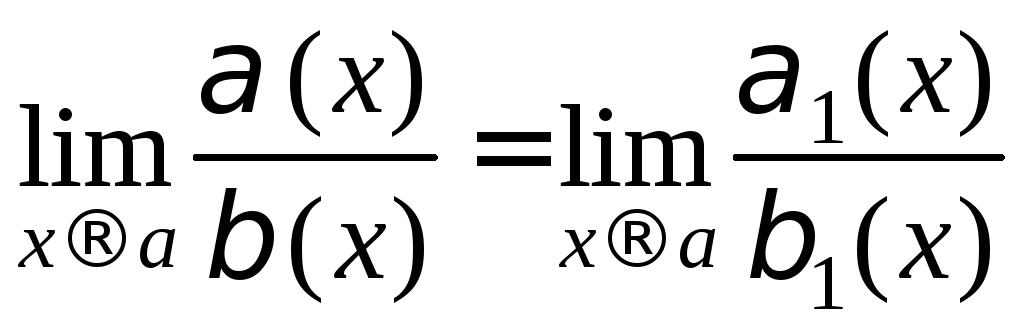

Доказательство.

Всправедливо:.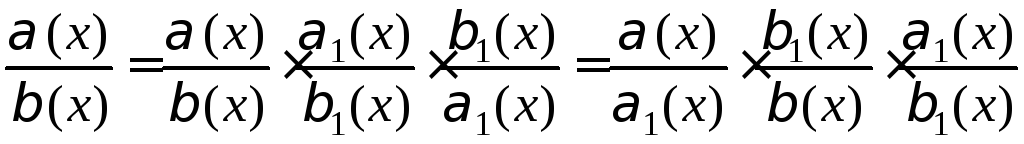

Так как существует , существуети существует, то существует.

Практическое применение теоремы 3 заключается в следующем.

При нахождении предела отношения двух бесконечно малых функцийкаждую из них можно заменить любой эквивалентной бесконечно малой функцией, и от этого предел не изменится.

Пример 4.а); б).

Замечание.В тех случаях, когда в числителе или знаменателе стоит сумма, при раскрытии неопределенностинельзя заменять отдельные слагаемыеэквивалентными величинами, так как такая замена может привести к неверному результату или вовсе к потере смысла.

Пример 5.

.

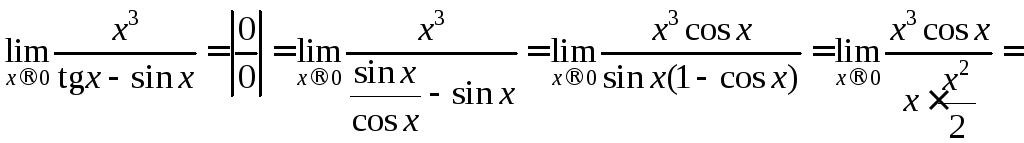
Но если бы мы сделали замену tgx~x, sinx~x, тоне имеет смысла.

Сравнение бесконечно больших функций

Пусть - бесконечно большие функции при.

Если (0), тобесконечно большая функциявысшего(низшего)порядкапо отношению к бесконечно большой функциипри.

Если , тои-бесконечно большие функцииодного порядка(еслиk=1 – тоэквивалентные бесконечно большие функции).

Для бесконечно большой функции можно сформулировать теорему, подобную теореме 3.

26