§ 17. Распространение теорем о пределах
последовательностей на случай функций
Все теоремы о пределах, доказанные для последовательностей (xn), применимы к функциям. Покажем обоснованность их переноса на функции. Для этого докажем несколько теорем.
Свойства функций, имеющих предел в точке
Теорема 1.(Единственность предела). Любая функция в точке может иметь только один предел.
Доказательство:
Пусть
,
и
.
Возьмем (xn):xn
a.
Рассмотрим (f(xn)).
По определению предела функции по Гейне
и
.
Но по теореме о единственности предела
последовательности отсюда следует, чтоА=В.
Полученное противоречие доказывает
теорему.
Теорема 2.Если
,
то
ограничена в некоторой проколотой
окрестности точкиа.
Доказательство.
:
:
выполняется
.
По определению ограниченной функции
это означает, что
ограничена в
.
Теорема 3.
тогда и только тогда, когда существует
окрестность
:
представима в виде
,
где
.
Доказательство аналогично случаю последовательностей («на языке -»).
Предельный переход в неравенствах
Теорема 4.Пусть 1)
;
2)
.
Тогда
.
Доказательство.
Выберем
.
Тогда по условию 2) теоремы
:
:
выполняется
,
:
:
выполняется
.
По условию 1) теоремы
:
выполнено
.
Положим
.
Тогда для выбранного
:
:
выполняется
.
Теорема 5.Пусть
,
иА<B(A>B).
Тогда
:
:
выполняется
(
).
Доказательство.
По
условию
:
:
выполняется
,
:
:
выполняется
.
Возьмём
и
.
Тогда
и, значит, для выбранного
:
:
выполняется
.
Теорема 6.Если
иА<B(A>B),
то
:
:
выполняется
(
).
Доказательство.
Пусть
.
По теореме 5 Þ
:
:
выполняется
.
Теорема 7.(Предельный переход в неравенствах)
Пусть
,
и
:
:
выполняется
).
Тогда
.
Доказательство от противного (Þиз теоремы 5).
Теоремы, связанные с арифметическими операциями над пределами
Теорема 8.Пусть
и
определены в некоторой проколотой
окрестности точкиа
и
,
.
Тогда в точкеасуществуют пределы
суммы, разности, произведения и частного
(при условии, что
и
в
),
причем
,
,
,
при
и
в
.
Доказательство.
Докажем
для суммы, остальное – аналогично.
Возьмём
:
.
Так как
и
,
то по определению предела функции по
Гейне
,
.
По теореме о пределе суммы последовательностей
последовательность
также имеет предел, причем
.
Получили, что
:
последовательность
сходится к числуА+В(
)
.
Следствие.Если
,
то
,
.
§ 18. Некоторые замечательные пределы
1.Первый замечательный предел
Лемма.
:
. (1)
Доказательство.
1)
.
В круге радиусом Rпостроим центральный угол с радианной меройx
(2)
из (2) 
.
(3)
,
,
верно (1)
2)
,
то есть для (-х) справедливо
.
Замечание 1.Так как прих=0,
,
,
то
:
справедливо
. (4)
Замечание 2:
(5)
Действительно,
(5) доказано для
.
имеет место неравенство
(5) верно
.
Рассмотрим функцию
,
.
.
Покажем, что
-замечательный
предел.
справедливо
неравенство
(1)
Разделим (1) на
>0:
или
.
;
.
.
Умножим все части на (-1): 
.
Прибавим ко всем частям 1: 
.
Так как
и
,
то
(6).
Согласно определению для выбранного
надо найти
,
выполнено
. (7)
Так как по (6)
,
то если выполнено
,
значит выполнено и (7).
Отсюда
,
.
Так как (6) справедливо на
,
то возьмем
.
Тогда
выполняется
.
Замечание.Из установленной оценки
(6) следует, что
.
Следствие 1.
.
Следствие 2.
.
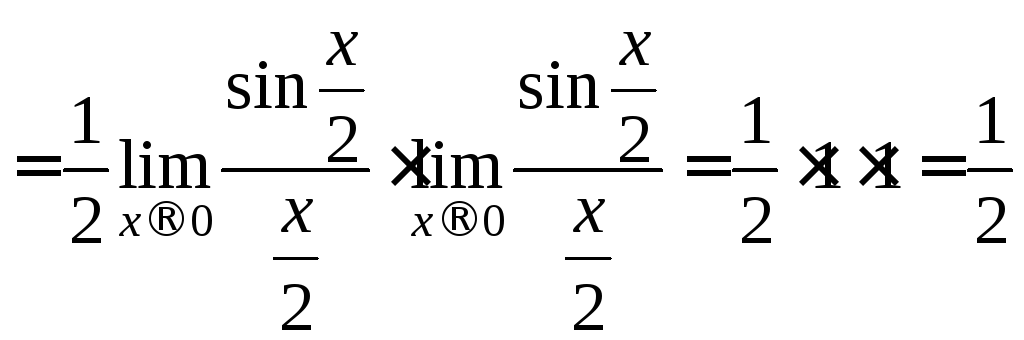Пример 1.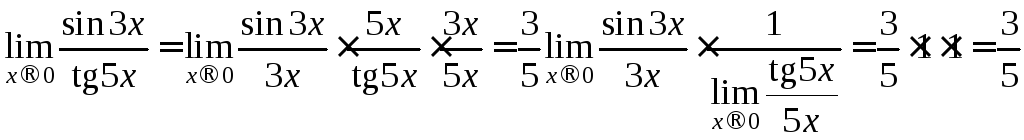
.
2.Предел сложной функции (замена переменной при вычислении пределов)
Теорема.Пусть
,
и
.
Пусть существует (конечный или бесконечный)
и
.
Тогда при
существует и предел (конечный или
бесконечный) сложной функции
,
причём
,
где
.
Пример 2. 
.
3.Второй замечательный предел
Рассмотрим функцию
,
.
Рассмотрим функцию f(x)
в
.
Докажем, что существует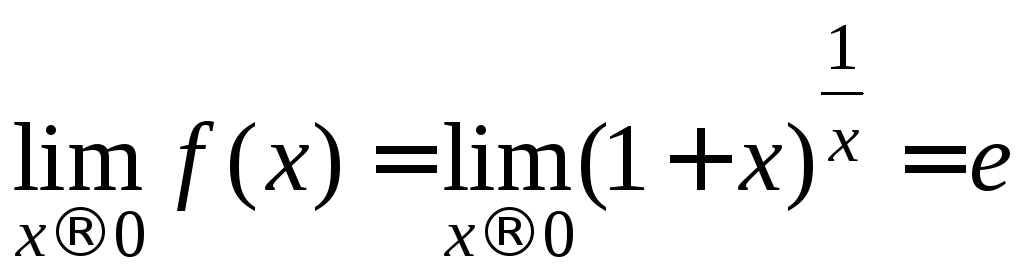
.
Замечание 1.Ранее было доказано,
что последовательность
сходится,
.
Тогда любая подпоследовательность
последовательности (yn)
также имеет предел, равныйе, то есть
.
— замечательный предел.
Доказательство.
1)
Выберем
.
Будем считать, что
выполнено
0<
<1.
Положим
,
или
(1)
Так как
,
то
.
Тогда из замечания 1 и теорем о пределах арифметических операций над последовательностями следует:
;
.
Отсюда по теореме о пределе промежуточной
последовательности из (1) следует, что
.
Итак,
;
выполняется
.
2) Возьмем
,
.
Положим
.
Тогда
,
.
Следовательно,
.
Таким образом,
,
выполняется
.
3) Из 1) и 2) по необходимому и достаточному
условию существования предела функции
(через односторонние пределы) 
.
Замечание 2.
(с помощью замены
)