§15. Предел функции

1. Предельная точка множества

Определение. Точка а называется предельной точкой множества D, если в любой окрестности точки а имеется хотя бы одна точка множества D, отличная от а, т.е.V(a) .

Пример. D=(0;2){-1;3}. Предельной точкой D является любая точка из [0;2].

Лемма. Для того, чтобы точка а была предельной точкой множества D, необходимо, чтобы существовала последовательность (х_n) точек из D, отличных от а и сходящаяся к а.

Доказательство.

1) Необходимость.

Выберем последовательность (δ_n): δ_n=,limδ_n=0. Т.к. а-предельная точка множества D, то в окрестности есть хотя бы одна точка, отличная ота.

δ₁=1x₁, x₁D,

δ₂=2x₂, x₂D,

……

δ_n=nx_n, x_nD.

Итак, Значит,. Так как, то по теореме о пределе промежуточной последовательности.

2) Достаточность.

Очевидно из геометрического смысла предела последовательности.

2. Первое определение предела функции в точке (по Гейне)

Пусть функция y=f(x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а, то есть f(x) определена в D(f).

Возьмем любую последовательность точек , принадлежащих:

(1),

такую, что (так кака – предельная точка , то по лемме такая последовательность существует). Последовательности (1) соответствует последовательность соответствующих значений функции

(2).

Например, f(x)=x², (x_n): x_n=, (f(x_n)): f(x_n)=.

Последовательность (2) может иметь предел, а может и не иметь. Из можно выделить и другие последовательности вида (1); всем им соответствуют последовательности вида (2).

Возможны 2 случая.

1 случай. , сходящейся ка () соответствующая последовательность значений функции (2) имеет один и тот же предел, равный A.

Пример 1.  ,D(f)=\

a=2. Пусть : -2. Выберем,, такую, что.

Рассмотрим (f(x_n)): f(x_n)=.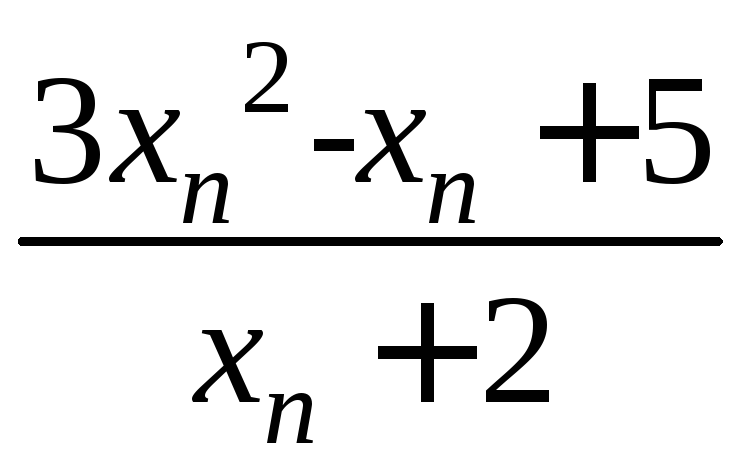

==(А=).

Получили, что для любой последовательности точек из,а=2, сходящейся к а=2, соответствующая последовательность значений функции (f(x_n)) сходится к А=.

2 случай. Для некоторых последовательностей (1) последовательности соответствующих значений функции (2) не имеют предела;

или для двух некоторых различных последовательностей (1), сходящихся к а, соответствующие последовательности (2) имеют различные пределы.

Пример 2.  , D(f)=,a=0. Рассмотрим .

Рассмотрим две последовательности и.

: ,n; ,,

: ; .

: , n; ,.

.

Определение 1 (по Гейне). Число А называется пределом функции f(x) в точке а (или при ха), если для любой последовательности (х_n) точек из , сходящейся к а, соответствующая последовательность значений функции (f(x_n)) сходится к числу А.

Обозначается или.

Таким образом, ,выполнено(f(x_n))A.

Согласно определению, в примере 1 . В примере 2 функцияне имеет предела в точке 0.

Замечание 1. Из определения 1 предела следует, что функция f может иметь в точке а только один предел.

Замечание 2. Из определения 1 предела следует, что значение функции в точке а (если оно существует), а также значения функции в точках, лежащих вне любой окрестности точки а, не влияют на существование и величину предела функции в точке а. Существование и величина предела функции в точке а зависит только от значений функции в сколь угодно малых окрестностях .

Замечание 3. Если f(x)=g(x), то функции f и g одновременно имеют или не имеют предел в точке а; если имеют, то эти пределы равны.

Замечание 4. Если функция f имеет предел при xа, то она определена в некоторой .

Определение предела по Гейне основано на понятии числовой последовательности. Поэтому его называют определением “на языке последовательностей”.

Замечание 5. Определение по Гейне удобно использовать для доказательства того, что f(x) не имеет предела в точке x₀. Для этого достаточно указать какую-либо последовательность (f(x_n)), не имеющую предела, или указать две последовательности и, имеющие различные пределы (см. пример 2).