
Lek_1_ELEKTROSTATIKA
.pdf
С учетом этих замечаний формулу (27) запишем в виде:
|
|
q1 |
|
2 |
d |
||
dФ1 |
|
|
|
r |
|||
4 |
0 |
r2 |
|||||
|
|
|
|
||||
|
|
|
|
|
|
|
|
или
dФ |
q |
d |
|
1 |
|||
|
|
||
1 |
4 |
|
|
|
0 |
||
|
|
(28)
• Формула (28) представляет элементарный поток
вектора напряженности электрического поля через элемент dS замкнутой поверхности S, обусловленный зарядом q1
А поток Ф1 через всю замкнутую поверхность:
|
q1 |
4 |
q1 |
|
Ф1 |
d |
|||
4 0 |
0 |
|||
|
0 |

или |
|
|
|
|
Ф |
q |
|
||
|
|
|||
|
|
1 |
(29) |
|
|
|
|
||
|
1 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
• Добавляя внутрь замкнутой поверхности S заряд q2,
получим дополнительный поток Ф2:
P |
Ф |
q2 |
(30) |
|
|||
2 |
0 |
|
|
|
|
|
• Добавляя заряд q3, получим дополнительный поток
Ф3: |
|
|
|
|
|
Ф |
q |
|
|
||
|
|
3 |
и т.д. |
(31) |
|
|
|
|
|||
|
3 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||
• Положительные заряды |
создают положитльные |
||||
потоки, а отрицательные заряды – отрицательные потоки.

Для системы зарядов полный поток Ф:
|
|
|
|
|
|
||||||
|
Ф Ф Ф Ф ... |
||||||||||
|
|
|
1 |
|
2 |
|
|
3 |
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Ф |
i |
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
0 |
i 1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
или с учетом (26) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
n |
|
||
|
|
|
(E, dS ) |
|
i |
|
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
q |
|
||||
|
|
S |
|
|
|
|
0 |
i 1 |
|
||
|
|
|
|
|
|
|
|
||||
Формулы (32) и (33) являются выражением теоремы Гаусса.
(32)
(33)
аналитическим
Сформулируем эту теорему:
•Полный поток вектора напряжённости электростатического поля через любую замкнутую
поверхность охватывающую заряды равен
произведению величины 1 / 0 на алгебраическую сумму
зарядов, охватываемых этой поверхностью.
•Если заряды находятся не в вакууме, а в среде с
диэлектрической проницаемостью 0 , то формула,
выражающая теорему Гаусса будет иметь вид:
|
1 |
n |
|
|
(E, dS ) |
qi |
(34) |
||
|
||||
S |
0 |
i 1 |
||
|
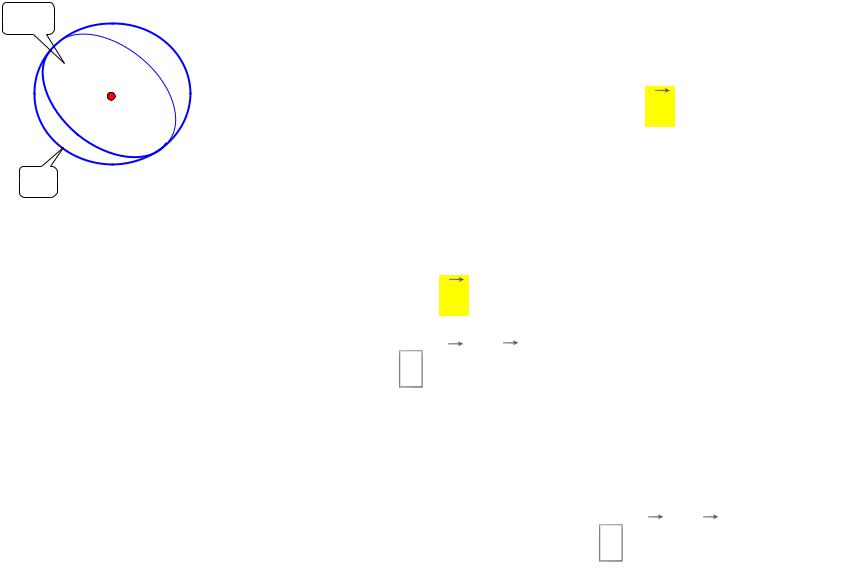
10. Теореме Гаусса в дифференциальной форме
V
P
S Рис. 12
• Пусть в некоторой области
пространства создано электростатическое поле – поле вектора E.
• Отметим в нём некоторую точку Р и
окружим эту точку замкнутой поверхностью S.
• Запишем поток вектора
E
через эту поверхность:
|
Ф (E, dS ) |
|
|
|
|
|
|
S |
|
|
|
|
|
• Обозначим через ∆V объём, охватываемый |
||||||
поверхностью S. |
|
|
|
|
|
|
|
1 |
|
(E, dS ) |
и возьмём |
||
• Сконструктируем выражение: |
||||||
|
||||||
V |
||||||
|
|
|||||
|
|
|
S |
|
|
|

его предел при ∆V → 0.
|
|
|
lim |
1 |
|
(E, dS) |
|
|
|
|||||
|
|
|
V |
|
|
|
||||||||
|
|
|
V 0 |
S |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
• Предел этого выражения при ∆V → 0 называется |
||||||||||||||
|
|
|
E |
|
|
|
|
|
|
|
||||
дивергенцией вектора |
|
(divE) |
. |
|
|
|
||||||||
Следовательно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
divE lim |
1 |
|
(E, dS ) |
(35) |
||||||||
|
|
V |
||||||||||||
|
|
|
|
V 0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|
величина скалярная. В декартовых координатах |
|||||||||||||
divE |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
divE |
Ex |
|
Ey |
|
Ez |
|
|
|||||
|
|
x |
|
z |
|
|
||||||||
|
|
|
|
|
dy |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
divE
есть мера источников поля.
Если
divE 0
то в
данной области пространства нет зарядов (заряды являются источниками поля).

• В тех точках поля, где |
divE 0 |
, поле создается поло- |
||
|
|
|
|
|
жительными зарядами, а там, где |
divE 0 |
, поле соз- |
||
|
||||
дается отрицательными зарядами (стоки, истоки).
 q
q 
 q
q 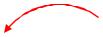
|
Рис. 13 |
|
Рис. 14 |
||
|
|
|
|
|
|
|
divE 0 |
divE 0 |
|||
Исток линий напряжен- |
Сток линий напряжен- |
||||
|
ности. |
|
ности. |
||
• Если divE 0, то в данной |
области пространства |
||||
электрические заряды отсутствуют.

• Сформулируем понятие дивергенции поля вектора
E
.
• Дивергенцией вектора E электростатического поля
в некоторой его точке называется предел, к которому стремится отношение потока вектора E через малую
поверхность, охватывающую данную точку к объему, заключенному внутри этой поверхности при его стремлении к нулю.
• Полагая, что в объеме ∆V
средней объемной плотностью запишем в виде:
заряд |
распределен со |
||
|
|
|
|
|
|
, |
теорему Гаусса |
|
|
||
|
|
|
|
(E, dS) |
1 |
V , |
|
||
S |
0 |
|
откуда

|
1 |
(E, dS) |
1 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
V |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
S |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
• При стремлении объема ∆V → 0, т.е. при стягивании |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
его к точке средняя плотность заряда |
|
|
|
|
будет |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стремиться к плотности |
|
|
в данной точке |
|
( |
|
) |
. |
|||||||||||||||
|
|
||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
1 |
(E, dS ) |
1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
V 0 V |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или с учетом формулы (35) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
divE |
1 |
|
|
|
|
|
|
|
|
|
|
|
(36) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
•Формула (36) выражает теорему Гаусса в дифференциальной форме.
•Следует знать, что в общем случае (x, y, z).

• Если заряд распределен по объему, охватываемому замкнутой поверхностью S, с объемной плотностью ,
то формула (33), выражающая теорему Гаусса может быть представлена в виде:
|
(E, dS ) |
|
|
1 |
dV |
|
||||||||
|
|
|
|
|
||||||||||
|
S |
|
|
|
|
0 |
|
V |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или |
(E, dS ) |
1 |
|
dV |
(37) |
|||||||||
|
|
|
|
|||||||||||
|
|
|
|
|||||||||||
|
|
|
|
|||||||||||
|
S |
|
|
|
V |
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
однако |
|
1 |
divE |
|
|
|||||||||
|
|
|
|
|
||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С учетом этой формулы формулу (37) запишем в виде:
(E, dS ) divEdV |
(38) |
|
S |
V |
|
