Advanced Wireless Networks - 4G Technologies

19.5.5 Network with memory

In this case we have to slightly modify the associated acyclic network.

Definition 1

Given a communication network (G, S) and a positive integer τ , the associated communication network with memory, denoted as (G[τ ], S), is defined as follows. The set of nodes in G[τ ] includes the node S and all pairs of the type [X, t], where X is a nonsource node in G and t ranges through integers 1 to τ . Channels in the network (G[τ ], S) belong to one of the three types listed below. For any nonsource nodes X and Y in (G, S);

(1)for t ≤ τ , the multiplicity of the channel from S to [X, t] is the same as that of the channel S X in the network (G, S);

(2)for t < τ , the multiplicity of the channel from [X, t] to [Y, t + 1] is the same as that of the channel X Y in the network (G, S);

(3) for t < τ , the multiplicity of channels from [X, t] to [X, t + 1] is equal to t ×

mf G(X).

(4)The communication network (G[τ ], S) is acyclic.

(5)Every flow from the source to the node X in the network (G(τ ), S) corresponds to

aflow with the same volume from the source to the node [X, t] in the network (G[τ ], S).

(6)Every LCM v on the network (G(τ ), S) corresponds to an LCM u on the network (G[τ ], S) such that for all nodes X in G: dim[u([X, τ ])] = dim[v(X)].

19.5.6 Construction of a generic LCM on an acyclic network

Let the nodes in the acyclic network be sequentially indexed as X0 = S, X1, X2, . . . , Xn such that every channel is from a smaller indexed node to a larger indexed node. The following procedure constructs an LCM by assigning a vector v(XY ) to each channel XY , one channel at a time.

{

for all channels XY

v(X Y ) = the zero vector; // initialization for ( j = 0; j ≤ n; j + +)

{

arrange all outgoing channels X j Y from X j in an arbitrary order;

take one outgoing channel from X j at a time

{

let the channel taken be X j Y ;

choose a vector w in the space v(X j ) such that w v(U Z ) : U Z ξ for any collection ξ of at most d − 1 channels with

780 NETWORK INFORMATION THEORY

v(X j ) v(U Z ) : U Z ξ ; v(X j Y ) = w;

}

v(X j+1) = the linear span by vectors

v(X X j+1) on all incoming channels X X j+1 to X j+1;

}

}

The essence of the above procedure is to construct the generic LCM iteratively and make sure that in each step the partially constructed LCM is generic.

19.5.7 Time-invariant LCM and heuristic construction

In order to handle delays, we can use an element a(z) of F[(z)] to represent the z-transform of a stream of symbols a0, a1, a2, . . . , at , . . . that are sent on a channel, one symbol at a time. The formal variable z is interpreted as a unit-time shift. In particular, the vector assigned to an outgoing channel from a node is z times a linear combination of the vectors assigned to incoming channels to the same node. Hence a TILCM is completely determined by the vectors that it assigns to channels. On the communication network illustrated in Figure 19.18, define the TILCM v as

v(S X) = (1 0)T, v(SY ) = (0 1)T, v(X Y ) = (z z3)T v(Y W ) = (z2 z)T and v(W X) = (z3 z2)

By formal transformation we have for example

v(X Y ) = (z z3) = z(1 − z3)(1 0)T + z(z3 z2)T

=z[(1 − z3)v(S X) + v(W X)]

Thus, v(X Y ) is equal to z times the linear combination of v(S X) and v(W X) with coefficients 1 − z3 and 1, respectively. This specifies an encoding process for the channel X Y that does not change with time. It can be seen that the same is true for the encoding process of every other channel in the network. This explains the terminology ‘time-invariant’ for an LCM.

To obtain further insight into the physical process write the information vector as [a(z) b(z)], where

belong to F[(z)]. The product of the information (row) vector with the (column) vector assigned to that channel represents the data stream transmitted over a channel

= za(z) + z3b(z) → (0, a0, a1, a2 + b0, a3 + b1, a4 + b2, . . . , at−1 + bt−3, . . .)[a(z) b(z)] · v(Y W )

= z2a(z) + zb(z) → (0, b0, a0 + b1, a1 + b2, a2 + b3, a3 + b4, . . . ,

at−2 + bt−1, . . .)[a(z) b(z)] · v(W X)

=z3a(z) + z2b(z) → (0, 0, b0, a0 + b1, a1 + b2, a2 + b3, . . . , at−3 + bt−2, . . .)

Adopt the convention that at = bt = 0 for all t < 0. Then the data symbol flowing over the channel X Y , for example, at the time slot t is at−1 + bt−3 for all t ≥ 0. If infinite loops are allowed, then the previous definition of TILCM v is modified as follows:

v(S X) = (1 0)T , v(SY ) = (0 1)T

v(XY ) = (1 − z3)−1(z z3)T, v(Y W ) = (1 − z3)−1(z2 z)T

and

v(W X) = (1 − z3)−1(z3 z2)

The data stream transmitted over the channel X Y , for instance, is represented by

a j z j b j z j · v(X Y ) = (a j z j+1 + b j z j+3)/(1 − z3)

That is, the data symbol at−1 + at−4 + at−7 + · · · + bt−3 + bt−6 + bt−9 + · · · is sent on the channel X Y at the time slot t. This TILCM v, besides being time invariant in nature, is a ‘memoryless’ one because the following linear equations allows an encoding mechanism that requires no memory:

and

v(W X) = zv(Y W )

19.5.7.1 TILCM construction

There are potentially various ways to define a generic TILCM and, to establish desirable dimensions of the module assigned to every node. In this section we present a heuristic construction procedure based on graph-theoretical block decomposition of the network. For the sake of computational efficiency, the procedure will first remove ‘redundant’ channels from the network before identifying the ‘blocks’ so that the ‘blocks’ are smaller. A channel in a communication network is said to be irredundant if it is on a simple path starting at the source. otherwise, it is said to be redundant. Moreover, a communication network is said to be irredundant if it contains no redundant channels. In the network illustrated in Figure 19.19, the channels Z X, T X and T Z are redundant.

The deletion of a redundant channel from a network results in a subnetwork with the same set of irredundant channels. Consequently, the irredundant channels in a network define an

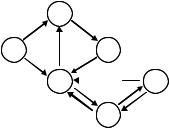
782 NETWORK INFORMATION THEORY

Y

X T

Z

Figure 19.19 Redundant channels in a network.

irredundant subnetwork. It can be also shown that, if v is an LCM (respectively, a TILCM) on a network, then v also defines an LCM (respectively, a TILCM) on the subnetwork that results from the deletion of any redundant channel. In addition we say that two nodes are equivalent if there exists a directed path leading from one node to the other and vice versa. An equivalence class under this relationship is called a block in the graph. The source node by itself always forms a block. When every block ‘contracts’ into a single node, the resulting graph is acyclic. In other words, the blocks can be sequentially indexed so that every interblock channel is from a smaller indexed block to a larger indexed block.

For the construction of a ‘good’ TILCM, smaller sizes of blocks tend to facilitate the computation. The extreme favorable case of the block decomposition of a network is when the network is acyclic, which implies that every block consists of a single node. The opposite extreme is when all nonsource nodes form a single block exemplified by the network illustrated in Figure 19.19. The removal of redundant channels sometimes serves for the purpose of breaking up a block into pieces. For the network illustrated in Figure 19.19, the removal of the three redundant channels breaks the block {T, W, X, Y, Z } into the three blocks

{T }, {W, X, Y } and {Z }.

In the construction of a ‘good’ LCM on an acyclic network, as before, the procedure takes one node at a time according to the acyclic ordering of nodes and assigns vectors to outgoing channels from the taken node. For a general network, we can start with the trivial TILCM v on the network consisting of just the source and then expand it to a ‘good’ TILCM v that covers one more block at a time.

The sequential choices of blocks are according to the acyclic order in the block decomposition of the network. Thus, the expansion of the ‘good’ TILCM v at each step involves only incoming channels to nodes in the new block. A heuristic algorithm for assigning vectors v(X Y ) to such channels XY is for v(XY ) to be z times an arbitrary convenient linear combination of vectors assigned to incoming channels to X. In this way, a system of linear equations of the form of Ax = b is set up, where A is a square matrix with the dimension equal to the total number of channels in the network and x is the unknown column vector whose entries are v(XY ) for all channels XY . The elements of A and b are polynomials in z. In particular, the elements of A are either ±1, 0, or a polynomial in z containing the factor z. Therefore, the determinant of A is a formal power series with the constant term (the zeroth power of z) being ±1, and, hence is invertible in F(z). According to Cramer’s rule, a unique solution exists. This is consistent with the physical intuition because the whole network is completely determined once the encoding process for each channel is specified. If this unique solution does not happen to satisfy the requirement for being a ‘good’ TILCM, then

the heuristic algorithm calls for adjustments on the coefficients of the linear equations on the trial-and-error basis.

After a ‘good’ TILCM is constructed on the subnetwork formed by irredundant channels in a given network, we may simply assign the zero vectors to all redundant channels.

Example

After the removal of redundant channels, the network depicted by Figure 19.19 consists of four blocks in the order of {S}, {W, X, Y }, {Z } and {T }. The subnetwork consisting of the first two blocks is the same as the network in Figure 19.18. When we expand the trivial TILCM on the network consisting of just the source to cover the block {W, X, Y }, a heuristic trial would be

v(S X) = (1 0)T v(SY ) = (0 1)T

together with the following linear equations:

v(X Y ) = zv(S X) + zv(W X) v(Y W ) = zv(SY ) + zv(XY )

and

v(W X) = zv(Y W ).

The result is the memoryless TILCM v in the preceding example. This TILCM can be further expanded to cover the block {Z } and then the block {T }.

19.6 CAPACITY OF WIRELESS NETWORKS USING MIMO TECHNOLOGY

In this section an information theoretic network objective function is formulated, which takes full advantage of multiple input multiple output (MIMO) channels. The demand for efficient data communications has fueled a tremendous amount of research into maximizing the performance of wireless networks. Much of that work has gone into enhancing the design of the receiver, however considerable gains can be achieved by optimizing the transmitter.

A key tool for optimizing transmitter performance is the use of channel reciprocity. Exploitation of channel reciprocity makes the design of optimal transmit weights far simpler . It has been recognized that network objective functions that can be characterized as functions of the output signal-to-interference noise ratio (SINR) are well suited to the exploitation of reciprocity, since it permits us to relate the uplink and downlink objective functions [48–50]. It is desirable, however, to relate the network objective function to information theory directly, rather than ad-hoc SINR formulations, due to the promise of obtaining optimal channel capacity. This section demonstrates a link between the information theoretic, Gaussian interference channel [51] and a practical network objective function that can be optimized in a simple fashion and can exploit channel reciprocity. The formulation of the objective function permits a water filling [52] optimal power control solution, that can exploit multipath modes, MIMO channels and multipoint networks.

Consider the network of transceivers suggested by Figure 19.20. Each transceiver is labeled by a node number. The nodes are divided into two groups. The group 1 nodes transmit in a given time-slot, while the group 2 nodes receive. In alternate time-slots, group

784 NETWORK INFORMATION THEORY

Figure 19.20 Network layout.

2 nodes transmit, while group 1 nodes receive, according to a time division duplex (TDD) transmission scheme.

The channel is assumed to be channelized into several narrow band frequency channels, whose bandwidth is small enough so that all multipath is assumed to add coherently. This assumption allows the channel between any transmit antenna and any receive antenna to be modeled as a single complex gain and is consistent with an orthogonal frequency division multiplexing (OFDM) modulation scheme. All transceivers are assumed to have either multiple antennas or polarization diversity, for both transmit and receive processing. The link connecting nodes may experience multipath reflections. For this analysis we assume that the receiver synchronizes to a given transmitter and removes any propagation delay offsets. The channel, for a given narrow band, between the transmitter and receiver arrays is therefore modeled as a complex matrix multiply.

Let 1 be an index into the group 1 transceivers, and 2 an index into the group 2 transceivers. When node 2 is transmitting during the uplink, we model the channel between the two nodes as a complex matrix H12( 1, 2) of dimension M1( 1) × M2( 2), where M1( 1) is the size of the antenna array at node 1, and M2( 2) is the size of the array at node 2. Polarization diversity is treated like additional antennae. In the next TDD time slot, during the downlink, node 1 will transmit and the channel from 1 to 2 is described by the complex M2( 1) × M1( 2) matrix H21( 2, 1). For every node pair ( 1, 2) that forms a communications link in the network, we assign a MIMO channel link number, indexed by k or m, in order to label all such connections established by the network. Obviously not every node pair is necessarily assigned a link number, only those that actually communicate. We also define the mapping from the MIMO link number to the associated group 1 node, 1(k) and the associated group 2 node 2(k) by the association of k with the link [ 1(k), 2(k)]. Because each channel is MIMO, a given node will transmit multiple symbols over possibly more than one transmission mode. The set of all transmission modes over the entire network is indexed by q and p. This index represents all the symbol streams that are transmitted from one node to another and therefore represents a lower level link number. The low level link numbers will map to its MIMO channel link, via the mapping k(q). Because our network will

786 NETWORK INFORMATION THEORY

as [52, 53]:

where, Gt ↔ {gt (q)} represents all transmit weights stacked into a single parameter vector and where we neglect the n dependency for the random vectors xr (n; k) and dt (n; k). The interference and the signal covariance matrices are defined as:

and where Rεr εr (k) is the covariance of the background noise vector εr (n, k). The covariance of the source statistics is assumed governed by the transmit weights Gt (k), therefore the covariance of dt (k) is assumed to be the identity matrix.

Let us now consider the introduction of complex linear beam-forming weights at the receiver. For each low level link q, we assign a receive weight vector wr (q), r {1, 2} for use at receiver r [k(q)]. The weights, in theory, are used to copy the transmitted information symbol,

and k(q j ) = k. The vector version of this can be written as:

and k(q j ) = k. The structure of the transceiver channel model is illustrated in Figure 19.21 for the uplink case, highlighting the first Mc(k) low-level links, all assumed to be associated with the same MIMO-channel link. The MIMO channel link index k and sample index n are omitted for simplicity. The downlink case is the same after the 1 and 2 indices are swapped.

Owing to the additional processing [52], the mutual information either remains the same or is reduced by the application of the linear receive weights,

g1(1) g1(2) g1(Mc)

d1(1) d1(2) d1(Mc)

Figure 19.21 Uplink transceiver channel model.

In addition to inequality, Equation (19.75), it can be also shown [54, 55] that, if the source symbols dt (q) are mutually independent then,

q: k(q)=k

The lower bound of in Equation (19.76) is referred to as the decoupled capacity and can be written as:

q: k(q)=k

where the collection of all receive weights is stacked into the parameter vector Wr ↔ {wr (q)}. Equations (19.75) and (19.76) demonstrate that

The decoupled capacity is implicitly a function of the transmit weights gt (q) and the receive weights wr (q). Optimizing over these weights can always acheive the full capacity of the Gaussian interference channel and hence the upper bounds in Equation (19.78).

First we write ˆt ( ; ) as, d n q