Advanced Wireless Networks - 4G Technologies

768 NETWORK INFORMATION THEORY

cooperation strategy operate at the physical layer. In OLA framework, the receiver has to solve an equivalent point-to-point communication problem without requiring higher layers’ interventions (MAC or network layer). The benefits from eliminating two layers are higher connectivity and faster flooding. However, the OLA flooding algorithm cannot be used for some broadcasting applications such as route discovery due to the fact that the higher layer information is eliminated.

Each node in the OLA is assumed to have identical transmission resources; therefore, any node has the ability of assuming the role of a leader. The leader can be chosen to be the leader of a troop, the clusterheads in clustering algorithms, or simply some node that has information to send.

19.4.3 Simulation environment

Various network broadcasting methods were analyzed using the ns2 network simulator. The simulation parameters are specified in Table 19.1 [40, 44]. Physical layer resources of the IEEE 802.11 DSSS PHY specifications [45] for the 2.4 GHz carrier were used. Each node-to-node transmission is assumed to experience independent small-scale fading with Rayleigh coefficients of variance 1. The large-scale fading is deterministic, and the path loss model is based on the model used in ns2 [46], where the free space model is used for distance d < dc (the cross-over distance) and the two-ray ground reflection model is used for d > dc, where dc = 4π/λ. The position of the ‘leader’ is randomly selected, and the OLA is regenerative.

There are three parameters that define the simulation setting. The first is the point- to-point average SNR (averaged over the small scale fading), which is defined as

using the specified path loss model. The exact SNR at each node is different due to the accumulation of signals. Therefore, we define a third parameter, which is the node SNR at the

detection level SNR gi 2/E ni 2 .The value of SNR can be mapped one-to-one det = || || {|| || } det

into the node error rate if error propagation is neglected and provides a criterion equivalent to the one in definition 1 to establish whether a node is connected or not. In all cases, the threshold on SNRdet is the same as the required point-to-point SNRp2 p(d) used to define network links in conventional networks, and let this value be ξ .

To simplify the network simulations, it is assumed that the transmission propagates through the network approximately in a multiple ring structure shown in Figure 19.13. In

Table 19.1 Simulation parameters

r

r

Dk

rk

Figure 19.13 Nodes in the ring r transmit approximately simultaneously.

Number of users

Figure 19.14 Connectivity ratio vs number of nodes in the network.

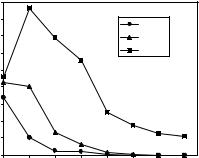
each ring, we prune away the nodes that do not have strong enough SNRdet, but we do not detect and retransmit at the exact time when the SNRdet reaches the threshold. Because we just partition the network geographically, we can expect, in general, nonuniform and lower error rates than the ones prescribed by the threshold on SNRdet. In the experiments, it was assumed that the signal space is perfectly estimated at each relaying node. This assumption is practical, because the network is static, and when the number of training symbols is sufficiently large, the noise variance caused by the contribution of the estimation error can be neglected. Figure 19.14 shows to what degree the network is connected according to definition 1 when the threshold for (SNRdet)dB is 10 dB. Specifically, the connectivity ratio

(CR) is shown, which is defined as the number of nodes that are ‘connected’, over the total number of nodes in the network. The nodes’ transmit power and thermal noise are constant and are fixed so that (SNRp2 p )dB = 10 at the distances dp2 p = 100, 80 and 60 m, representing the transmission radii.

For dp2 p = 100 m, the CR is 100 % even at very low node density. As we shorten the radius of transmission, the connectivity of the network will decrease. Figure 19.15 plots the delivery ratio (DR), which is defined as the ratio between the average number of nodes that receive packets using a specific flooding algorithm over the number of nodes that are connected in multiple hops, i.e. nodes for which there exists a path from the leader that is formed with point-to-point links having SNRp2 p above a fixed threshold. The only cause of packet loss considered in Williams and Camp [44] is the fact that the packet is not delivered because it is dropped by the intermediate relays’ queues to reduce the nodes congestion.

Routing, MAC and physical layer errors and their possible propagation are ignored in the

770 NETWORK INFORMATION THEORY

Number of users

Figure 19.15 Delivery ratio vs number of nodes in the network.

definition of DR. DR essentially shows how routing and MAC problems can reduce the probability of successfully reaching the nodes. Hence, according to Williams and Camp [44], the simple flooding algorithm achieves 100 % DR, even if it might create longer delays and instability due to the increased level of traffic. In the OLA, the accumulation of signal energy may still allow extra nodes (besides the ones that have a multihop route) to receive the broadcasted packets reliably. Therefore, if we calculate the ratio between the number of nodes connected in the OLA according to definition 1 and the number of nodes that are connected through multihop point-to-point links, we must be able to achieve more than 100 % DR. Using the parameters in Table 19.1, Figure 19.15 plots the DR vs the number of nodes. It is shown that there can be remarkable gains in connectivity over any scheme operating solely on point-to-point links.

The end-to-end delay is the time required to broadcast the packet to the entire network. In the OLA flooding algorithm, there is no channel contention, and therefore, the overhead necessary for carrier sensing and collision avoidance used in IEEE 802.11 is eliminated. With the reduction of overheads and the time saved by avoiding channel contention, it is clear that the speed of flooding will be much higher than the traditional broadcasting methods. Figure 19.16 shows the end-to-end delay vs the number of nodes in the network. The end-to-end delay is only in the order of milliseconds for a packet payload of 64 bytes, which coincides with the symbol period Ts times the number of bits in a packet.

19.5 NETWORK CODING

In this section we consider a communication network in which certain source nodes multicast information to other nodes on the network in multihops where every node can pass on any of its received data to others. The question is how the data should be sent and how fast each node can receive the complete information. Allowing a node to encode its received data before passing it on, the question involves optimization of the multicast mechanisms at the nodes. Among the simplest coding schemes is linear coding, which regards a block of data as a vector over a certain base field and allows a node to apply a linear transformation to a vector before passing it on.

772 NETWORK INFORMATION THEORY

Unlike a conserved physical commodity, information can be replicated or coded. The notion of network coding refers to coding at the intermediate nodes when information is multicast in a network. Let us now illustrate network coding by considering the communication network depicted in Figure 19.17(b). Again, we want to multicast two bits b1 and b2 from the source S to both the nodes Y and Z . A solution is to let the channels ST, TW and TY carry the bit b1, channels SU, UW and UZ carry the bit b2, and channels WX, XY and XZ carry the exclusive-OR b1 b2. Then, the node Y receives b1 and b1 b2, from which the bit b2 = b1 (b1 b2) can be decoded. Similarly, the node Z can decode the bit b1 from b2 and b1 b2 as b1 = b2 (b1 b2). The coding/decoding scheme is assumed to have been agreed upon beforehand. In order to discuss this issue in more detail, in this section we first introduce the notion of a linear-code multicast (LCM). Then we show that, with a ‘generic’ LCM, every node can simultaneously receive information from the source at rate equal to its max-flow bound. After that, we describe the physical implementation of an LCM, first when the network is acyclic and then when the network is cyclic followed by a presentation of a greedy algorithm for constructing a generic LCM for an acyclic network. The same algorithm can be applied to a cyclic network by expanding the network into an acyclic network. This results in a ‘time-varying’ LCM, which, however, requires high complexity in implementation. After that, we introduce the time-invariant LCM (TILCM).

Definition 1

Over a communication network a flow from the source to a nonsource node T is a collection of channels, to be called the busy channels in the flow, such that: (1) the subnetwork defined by the busy channels is acyclic, i.e. the busy channels do not form directed cycles; (2) for any node other than S and T, the number of incoming busy channels equals the number of outgoing busy channels; (3) the number of outgoing busy channels from S equals the number of incoming busy channels to T. The number of outgoing busy channels from S will be called the volume of the flow. The node T is called the sink of the flow. All the channels on the communication network that are not busy channels of the flow are called the idle channels with respect to the flow.

Definition 2

For every nonsource node T on a network (G, S), the maximum volume of a flow from the source to T is denoted max f lowG (T ), or simply mf(T) when there is no ambiguity.

Definition 3

A cut on a communication network (G, S) between the source and a nonsource node T means a collection C of nodes which includes S but not T . A channel XY is said to be in the cut C if X C and Y C. The number of channels in a cut is called the value of the cut.

19.5.1 Max-flow min-cut theorem (mfmcT)

For every nonsource node T , the minimum value of a cut between the source and a node T is equal to mf (T). Let d be the maximum of mf (T) over all T. In the sequel, the symbolwill denote a fixed d-dimensional vector space over a sufficiently large base field. The

information unit is taken as a symbol in the base field. In other words, one symbol in the base field can be transmitted on a channel every unit time.

Definition 4

An LCM v on a communication network (G, S) is an assignment of a vector space v(X) to every node X and a vector v(XY ) to every channel XY such that (1) v(S) = ; (2) v(XY ) v(X) for every channel X Y ; and (3) for any collection of nonsource nodes in the network {v(T ) : T } = {v(XY ) : X Y }. The notation · is for linear span. Condition (3) says that the vector spaces v(T ) on all nodes T inside together have the same linear span as the vectors v(XY ) on all channels XY to nodes in from outside .

LCM v data transmission: The information to be transmitted from S is encoded as a d-dimensional row vector, referred to as an information vector. Under the transmission mechanism prescribed by the LCM v, the data flowing on a channel XY is the matrix product of the information (row) vector with the (column) vector v(XY). In this way, the vector v(XY) acts as the kernel in the linear encoder for the channel XY. As a direct consequence of the definition of an LCM, the vector assigned to an outgoing channel from a node X is a linear combination of the vectors assigned to the incoming channels to X. Consequently, the data sent on an outgoing channel from a node X is a linear combination of the data sent on the incoming channels to X. Under this mechanism, the amount of information reaching a node T is given by the dimension of the vector space v(T) when the LCM v is used.

and

v(WX) = v(XY) = v(XZ) = (1 1)T

where ( )T stands for transposed vector. The data sent on a channel is the matrix product of the row vector (b1 b2) with the column vector assigned to that channel by v. For instance, the data sent on the channel WX is

(b1, b2)v(WX) = (b1, b2) (1 1)T = b1 + b2

Note that, in the special case when the base field of is GF(2), the vector b1 + b2 reduces to the exclusive-OR b1 b2 in an earlier example.

Proposition P1

For every LCM v on a network, for all nodes T dim[v(T )] ≤ m f (T ). To prove it fix a nonsource node T and any cut C between the source and T v(T ) v(Z ) : Z C =v(YZ) : Y C and Z C . Hence, dim[v(T )] ≤ dim( v(YZ) : Y C and Z C ), which is at most equal to the value of the cut. In particular, dim[v(T )] is upper-bounded

774 NETWORK INFORMATION THEORY

by the minimum value of a cut between S and T, which by the max-flow min-cut theorem is equal to mf(T).

This means that mf (T) is an upper bound on the amount of information received by T when an LCM v is used.

19.5.2 Achieving the max-flow bound through a generic LCM

In this section, we derive a sufficient condition for an LCM v to achieve the max-flow bound on dim[v(T )] in Proposition 1.

Definition

An LCM v on a communication network is said to be generic if the following condition holds for any collection of channels X1Y1, X2Y2, . . . , Xm Ym for 1 ≤ m ≤ d : ( ) v(Xk ) {v(X j Y j ) : j =k} for 1 ≤ k ≤ m if and only if the vectors v(X1Y1), v(X2Y2),

. . . , v(Xm Ym ) are linearly independent. If v(X1Y1), v(X2Y2), . . . , v(Xm Ym ) are linearly independent, then v(Xk ) {v(X j Y j ) : j =k} since v(Xk Yk ) v(Xk ). A generic LCM requires that the converse is also true. In this sense, a generic LCM assigns vectors which are

as linearly independent as possible to the channels.

With respect to the communication network in Figure 19.17(b), the LCM v defined by Equation (19.58) is a generic LCM. However, the LCM u defined by

Then u(S) u(WX) and u(W ) u(ST) , but u(ST) and u(WX) are not linearly independent. Therefore, u is not generic. Therefore, in a generic LCM v any collection of channels XY1, XY2, . . . , XYm from a node X with m ≤ dim[v(X)] must be assigned linearly independent vectors by v.

Theorem T1

If v is a generic LCM on a communication network, then for all nodes T, dim [v(T )] = mf(T ). To prove it, consider a node T not equal to S. Let f be the common value of mf(T ) and the minimum value of a cut between S and T . The inequality dim[v(T )] ≤ f follows from Proposition 1. So, we only have to show that dim[v(T )] ≥ f. To do so, let dim(C) = dim( v(X, Y ) : X C and Y C ) for any cut C between S and T . We will show that dim[v(T )] ≥ f by contradiction. Assume dim[v(T )] < f and let A be the collection of cuts U between S and T such that dim(U ) < f. Since dim[v(T )] < f implies V \{T } A, where v is the set of all the nodes in G, A is nonempty.

at least d, and dim({S}) = d ≥ f . Therefore, {S} A. Then there must exist a min-

can be seen as follows. The set of channels in cut U \{W } but not in K is given by {(X, W ) : X U \{W }}. Since v is an LCM v(X, W ) : X U \{W } v(W ). If v(W )

spanned by the channels in cut U \{W }, is contained by v(X, Y ) : (X, Y ) K . This implies that dim(U \{W }) ≤ dim(U ) < f is a contradiction. Therefore, for all W B, v(W )v(X, Y ) : (X, Y ) K . For all (W, Y ) K , since v(X, Z ) : (X, Z ) K \{(W, Y )}v(X, Y ) : (X, Y ) K , v(W ) v(X, Y ) : (X, Y ) K implies that v(W ) v(X, Z ) :

(X, Z ) K \{(W, Y )} .

Then, by the definition of a generic LCM {v(X Y ) : (X, Y ) K } is a collection of vectors such that dim(U ) = min(|K |, d). Finally, by the max-flow min-cut theorem, |K | ≥ f , and since d ≥ f, dim(U ) ≥ f . This is a contradiction to the assumption that U A. The theorem is proved.

An LCM for which dim[v(T )] = mf(T ) for all T provides a way for broadcasting a message generated at the source S for which every nonsource node T receives the message at rate equal to mf(T ). This is illustrated by the next example, which is based upon the assumption that the base field of is an infinite field or a sufficiently large finite field. In this example, we employ a technique which is justified by the following arguments.

Lemma 1

Let X, Y and Z be nodes such that mf(X) = i, mf(Y) = j, and mf(Z) = k, where i ≤ j and i > k. By removing any edge UX in the graph, mf(X) and mf(Y) are reduced by at most 1, and mf(Z) remains unchanged.

To prove it we note that, by removing an edge UX, the value of a cut C between the source S and node X (respectively, node Y ) is reduced by 1 if edge U X is in C, otherwise, the value of C is unchanged. By the mfmcT, we see that mf(X) and mf(Y) are reduced by at most 1 when edge UX is removed from the graph. Now consider the value of a cut C between the source S and node Z . If C contains node X, then edge UX is not in C, and, therefore, the value of C remains unchanged upon the removal of edge UX. If C does not contain node X, then C is a cut between the source S and node X. By the mfmcT, the value of C is at least i. Then, upon the removal of edge UX, the value of C is lower-bounded by i − 1 ≥ k. Hence, by the mfmcT, mf(Z) remains to be k upon the removal of edge UX.

Example E1

Consider a communication network for which mf(T ) = 4, 3 or 1 for nodes T in the network. The source S is to broadcast 12 symbols a1, . . . , a12 taken from a sufficiently large base field F. (Note that 12 is the least common multiple of 4, 3 and 1.) Define the set Ti = {T : m f (T ) = i}, for i = 4, 3, 1. For simplicity, we use the second as the time unit. We now describe how a1, . . . , a12 can be broadcast to the nodes in T4 ,T3, T1, in 3, 4 and 12 s, respectively, assuming the existence of an LCM on the network for d = 4, 3, 1.

sufficiently large because there are a finite number of nodes in T3. Define bi = αi r for i = 1, 2, 3. Now remove incoming edges of nodes in T4, if necessary, so that mf(T ) becomes 3 if T is in T4, otherwise, mf(T ) remains unchanged. This is based on Lemma 1). Let v2 be an LCM on the resulting network with d = 3. Let β = (b1 b2 b3) and transmit β as the information vector using v2 in the fourth second. Then all the nodes in T3 can recover β and hence α1, α2 and α3.

(3)Let s1 and s2 be two vectors in F3 such that {s1, s2} intersects with v2(T ) trivially for all T in T1, i.e. {s1,s2, v2(T )} = F3 for all T in T1. Define γi = βsi for i = 1, 2. Now remove incoming edges of nodes in T4 and T3, if necessary, so that mf(T ) becomes 1 if T is in T4 or T3, otherwise, mf(T ) remains unchanged. Again, this is based on Lemma 1). Now let v3 be an LCM on the resulting network with d = 1. In the fifth and the sixth seconds, transmit γ1 and γ2 as the information vectors using v3. Then all the nodes in T1 can recover β.

(4)Let t1 and t2 be two vectors in F4 such that {t1, t2} intersects with {r, v1(T )} trivially for all T in T1, i.e. {t1, t2, r, v1(T )} = F4 for all T in T1. Define δ1 = α1t1 and δ2 = α1t2. In the seventh and eighth seconds, transmit δ1 and δ2 as the information vectors using v3. Since all the nodes in T1 already know b1, upon receiving δ1 and δ2, α1 can then be recovered.

(5)Define δ3 = α2t1 and δ4 = α2t2. In the ninth and tenth seconds, transmit δ3 and δ4 as the information vectors using v3. Then α2 can be recovered by all the nodes in T1 .

(6)Define δ5 = α3t1 and δ6 = α0t2. In the eleventh and twelveth seconds, transmit δ5 and δ6 as the information vectors using v3. Then α3 can be recovered by all the nodes in T1.

So, in the ith second for i = 1, 2, 3, via the generic LCM v1, each node in T4 receives all four dimensions of αi , each node in T3 receives three dimensions of αi , and each node in T1 receives one dimension of αi . In the fourth second, via the generic LCM v2, each node in T3 receives the vector β, which provides the three missing dimensions of α1, α2 and α3 (one dimension for each) during the first 3 s of multicast by v1. At the same time, each node in T1 receives one dimension of β. Now, in order to recover β, each node in T1 needs to receive the two missing dimensions of β during the fourth second. This is achieved by the generic LCM v3 in the fifth and sixth seconds. So far, each node in T1 has received one dimension of αi for i = 1, 2, 3 via v1 during the first 3 s, and one dimension of αi for i = 1, 2, 3 from β via v2 and v3 during the fourth to sixth seconds. Thus, it remains to provide the six missing dimensions of α1, α2 and α3 (two dimensions for each) to each node in T1, and this is achieved in the seventh to the twelfth seconds via the generic LCM v3. The previous scheme can be generalized to arbitrary sets of max-flow values.