Лабораторная работа №53. Изучение затухающих и вынужденных гармонических колебаний крутильного маятника

Цель работы: 1. Изучение зависимости амплитуды механических колебаний от частоты внешнего воздействия.

2. Качественная проверка зависимости резонансной частоты от величины коэффициента затухания.

3. Определение резонансной частоты крутильного маятника.

Оборудования:

1) Крутильный маятник с постоянным магнитом.

2) Тахометр.

3) Автотрансформатор.

4) Секундомер.

Теоретическое введение

Гармоническими колебаниями называются процессы изменения состояния системы, обладающие той или иной степенью повторяемости. По физической природе колебания делятся на механические и электромагнитные. Примером механических колебаний являются колебания маятников, струн, мембран, столба воздуха в трубах и т.д. Электромагнитные колебания возникают в электрических цепях. В процессе колебаний периодически изменяются различные физические характеристики системы. В механической системе это смещение материальных точек относительно положения равновесия, скорость, ускорение, кинетическая и потенциальная энергия системы. Колебания, происходящие по закону синуса или косинуса, называются простейшими или гармоническими.

Основными физическими характеристиками колебательного движения являются амплитуда, период, частота, фаза.

Амплитуда А- величина наибольшего смещения тела от положения равновесия,

Период Т- время, за которое совершается одно полное колебание,

Частота - число колебаний за единицу времени,

(1)

Циклическая частота

Фаза колебания - величина, определяющая при заданной амплитуде состояние колебательной системы в любой момент времени. В механической системе фаза определяется смещение тела в любой момент времени.

(2)

где - начальная фаза колебаний (величина, определяющая начальное смещение).

Свободные не затухающие механические колебания возникают при выделении системы из положения равновесия однократным внешним воздействием и далее совершаются под действием внутренних сил упругой и квазиупругой природы. Квазиупругими называют силы не упругой природы, прямо пропорциональные величине смещения из положения равновесия.

Рассмотрим дифференциальное уравнение свободных не затухающих колебаний пружинного маятника массой m (рис.1).

Сила упругости, возникающая при деформации пружины, вызывает ускоренное движение маятника.

(3)

где k- коэффициент жесткости пружины, Х- смещение от положения равновесия.

По второму закону Ньютона:

(4)

где m – масса колеблющегося тела

mа _х= - kx (5)

где а_х = - ускорение этого тела.

(6)

т.к. k и m положительны, то их отношение выражается

(7)

где - собственная частота колебаний системы.

Дифференциальное уравнение колебаний такой системы имеет вид

(8)

Решением уравнений такого вида является гармоническая функция (закон собственных колебаний)

(9)

где А- амплитуда колебаний.

Период колебаний пружинного маятника равен.

(10)

Свободные затухающие колебания

Если в системе действуют диссипативные силы (силы трения), колебания становятся затухающими. По второму закону Ньютона имеем

ma_x=F_упр+F_тр (11)

где F_тр – сила трения равная

F_тр=r (12)

где r – коэффициент сопротивления среды,

–скорость колеблющегося тела.

Дифференциальное уравнение незатухающих колебаний записывается в виде

ma_x++kx=0 (13)

Это уравнение можно преобразовать, разделив почленно на m

(14)

дифференциальное уравнение затухающих гармонических колебаний.

Обозначим - называемый коэффициент затухания.

Решение дифференциального уравнения (закон затухающих колебаний) имеет вид

(15)

где - циклическая частота затухающих колебаний, связанная с частотой незатухающих колебаний и зависящая от свойств внешней среды.

(16)

Ввиду затухания такие колебания не являются строго периодическими. Под их периодом понимают интервал времени между двумя последовательными максимальными отклонениями от положения равновесия.

Амплитуда таких колебаний с течением времени убывает по экспоненциальному закону

(17)

где А₀ – начальная амплитуда,

е – основание натурального логарифма.

Быстроту затухания колебаний характеризуют физической величиной, называемой логарифмическим декрементом затухания , численно равен натуральному логарифму отношения амплитуд, отстоящих друг от друга по времени на период колебаний.

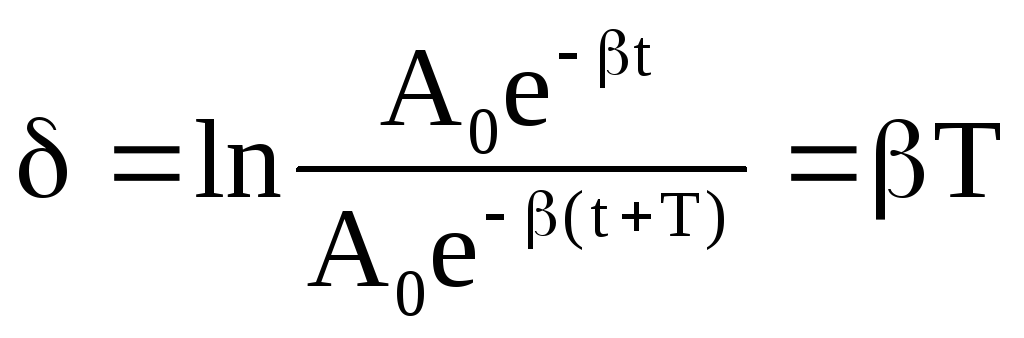(18)