umk-teoriya-mehanizmov

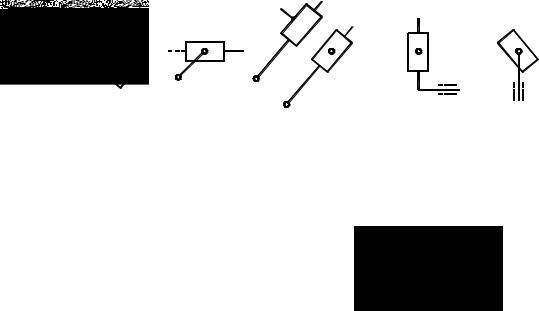
6.4.4. Статически определимые кинематические цепи

Рассматриваемую часть кинематической цепи передаточного меха- низма необходимо разбить на простейшие статически определимые кине- матические цепи. Эти цепи определяют при помощи формул Сомова-

Эти уравнения должны быть решены в целых числах. Первое урав- нение – сложное и для его решения используют ЭВМ. Второе уравнение решается проще. Полагая n = 1, p1 = 1, получим и p2 = 1, т.е. статической определимостью обладает звено с одной высшей и одной низшей кинема-

(количество звеньев n должно быть четным). Выражение (6.19) – струк- турная формула групп Ассура. Двухповодковых групп Асура (n = 2) суще- ствует 5 видов (рис. 6.12). Они различаются соотношением количества по- ступательных и вращательных кинематических пар.

Рис. 6.12. Виды двухповодковых групп Ассура

По Ассуру механизмы можно получить, присоединяя к началь- ным механизмам со степенью под- вижности W = 1 структурные груп- пы, либо цепи с нулевой степенью подвижности. Присоединением к начальному механизму структур- ной двухповодковой группы Ассу-

ра того или иного вида (рис. 6.12), получаем пять видов четырехзвенных

111

(простейших) рычажных механизмов. Шестизвенные схемы можно полу- чить, присоединяя по две двухповодковые, либо одну трехповодковую группы. Трехповодковая группа Ассура (рис. 6.13) имеет n = 4 и p1 = 6.

Трехповодковых групп – множество. В механизмах они встречаются редко, поскольку недостаточно изучены, а пересечение направлений трех поводков в одной точке приводит к заклиниванию механизма [21].

В нашем примере (рис. 6.11) механизм включает двухповодковую группу Ассура 4-5 (2-го вида), группу Ассура 2-3 (3-го вида) и главный вал, представляющий блок кривошипа 1 и зубчатого колеса z5, закреплен- ных на валу О.

6.4.5. Кинетостатика структурных групп

Рассмотрим пример механизма на рис. 6.10. Отсоединяем от меха- низма последнюю присоединенную группу Ассура 4-5 (рис. 6.14) и загру- жаем ее силами.

τ

Рис. 6.14. Последняя присоединенная группа 4-5 механизма на рис. 6.10, а

идействующие на нее силы

Вместах размыкания кинематических пар прикладываем реакции

Далее задачу решаем графически, строя план сил по уравнению:

112

ми направлениями. Строя многоугольник известных сил, замыкая его ли- ниями действия неизвестных, найдем эти неизвестные (рис. 6.15).

Далее отделяем группу 3-4 и загружаем ее силами веса, инерции, извест-

замыкающую многоугольника сил.

G3

C

Рис. 6.16. Предпоследняя присоединенная группа 2-3 и действующие на нее силы (без P )

03

113

Предварительно из уравнения равновесия всех сил, действующих на

находим P как замыкающую многоугольника первых четырех сил.

03

Рассмотрим главный вал, вместе с кривошипом ОА и зубчатым коле- сом z5 (рис. 6.17), представляющий статически определимую систему (од- но звено, высшая и низшая кинематические пары).

Рz45=Pур.

Рис. 6.17. Главный вал и действующие на него силы

Pz 45 = Pyp (направлена по линии зацепления зубьев, поддерживает ω1 ).

∑m0 = 0 : P21 × h21 × μ l −M И1 − Pz 45 × h45 × μl = 0 Pz 45 ,

затем P01 находим из плана сил:

P21 + G1 + Pz 45 + P01 = 0 .

Нами рассмотрен рычажный механизм и главный вал машины. Ме- ханизм имеет известный закон движения, известную силу полезных сопро- тивлений и состоит из трех статически определимых кинематических це- пей. Расчет продолжают и заканчивают начальным звеном машины – ро- тором приводного электродвигателя. Из равновесия ротора находят дви- жущий момент, который и обеспечивает главному валу движение с необ- ходимым значением δ .

Рассматривают все положения передаточного механизма, составляют таблицу изменения реакций, по ним конструируют кинематические пары, определяют потери на трение и износ.

114

7. ТРЕНИЕ И ИЗНОС В МАШИНАХ

7.1. Трение в кинематических парах

Материалы трущихся поверхностей и конструкции кинематических пар известны. Эти данные необходимы для оценки мощности сил трения в кинематических парах.

Во вращательной кинематической паре (рис. 7.1) мощность сил трения:

Nтр = Fтр × rц × wотн. ,

где Fтр = Рab × fпр – сила трения; Pab – реакция звена a на звено b;

fпр – приведенный коэффициент трения, зависящий от конструкции и материала элементов кинематической пары (выбирается по техническим справочникам);

ωотн – относительная угловая скорость:

ωотн = ωa − ωb = ω1(ωωa − ωωb ) ;

1 1

rц – радиус цапфы – поверхности сил трения.

а b

Рис. 7.1. К определению мощности сил трения во вращательной паре

В поступательной кинематической паре (рис. 7.2):

Рис. 7.2. Конструкции поступательной кинематической пары и приведенный коэффициент трения fпр

Мощность сил трения:

Nтр = Fтр ×Vотн.

Pab b

а

Vотн

Рис. 7.3. К определению мощности сил трения в поступательной паре

115

Относительная скорость скольжения:

V = Vab × w .

отн w1 1

Известно выражение среднециклового кпд:

по одной прямой).

Подставляя эти значения в формулу (7.1), получаем ηмгн. . Чтобы оп-

ределить кпд за цикл ηс.ц , необходимо такой расчет выполнить во всех по-

ложениях механизма. Тогда:

hmaxмгн + hminмгн = hс.ц.

2

Если значения ηс.ц сильно отличаются от принятого в начале проек-

тирования машины (по техническим справочникам), то расчет уточняется. По структуре суммы (7.2) оценивают сравнительную интенсивность износа кинематических пар. Большая интенсивность износа соответствует

большему значению Nтр i .

116

8.ОСНОВЫ ВИБРОЗАЩИТЫ ЧЕЛОВЕКА И МАШИНЫ

8.1.Дифференциальное уравнение малых колебаний машин

на фундаментах

Колебания конструкций с большой частотой называют вибрациями. Вибрации порождаются колебаниями с собственной частотой и с частотой возмущающей силы. Возмущающая сила может возникнуть как внутри машины (от неуравновешенных масс), так и извне (от фундамента). Вибрации вредно влияют на человека и приводят к разрушению конструк- ций, особенно при резонансах, когда амплитуда колебаний может возрасти теоретически до бесконечности. Они – одна из причин усталостных раз-

рушений деталей машин.

Вибрации ограничивают предельно допустимыми нормами. Способы борьбы – уравновешивание, виброгашение и виброизоляция. Виброизоля- ция предполагает введение амортизаторов, поглотителей и других объек- тов, способных рассеивать энергию колебаний за счет внутреннего трения. Силы в них зависят от скоростей.

Виброгашение – способ борьбы с колебаниями путем изменения параметров колебательной системы.

Механическим колебательным контуром называем совокупность массы и упругого основания (рис. 8.1). Рассмотрим систему «машина – уп- ругий фундамент, на котором она установлена» и защищающий амортиза- тор с коэффициентом вязкого трения β.

x

Рис. 8.1. Механический колебательный контур машины

Обозначим:

m – масса машины;

с – жесткость упругого основания; F – возмущающая сила;

F0 – амплитуда возмущающей силы; p – частота возмущающей силы.

117

Тогда дифференциальное уравнение малых колебаний машины в проекции на ось y от положения равновесия будет:

Величину с можно определить теоретически, либо экспериментально по прогибу фундамента f под известным весом машины mg при ее установ-

ке ( с = mg f ).

Из уравнения (8.1) при β = 0 (вязкое трение отсутствует) и F0 = 0 (нет возмущающей силы) получаем

myɺɺ+ сy = 0,

что представляет собой уравнение собственных колебаний машины на фундаменте с частотой

Если F ¹ 0 и правая часть уравнения (8.1) имеется, получаем урав- нение вынужденных колебаний машины с частотой р, которая при совпа- дении с величиной ω (резонанс) приводит к возрастанию амплитуды коле- баний до бесконечности.

При b ¹ 0 энергия колебаний рассеивается, и амплитуда их посте- пенно уменьшается.

Рассмотрим некоторые способы борьбы с вибрациями.

8.2. Защита воздействием на возмущающие силы

8.2.1.Уравновешивание роторов

Известно, что звенья машин совершают поступательное, вращательное, плоскопараллельное и др. движения. Рассмотрим звено, совершающее вра- щательное движение (ротор). Пусть в качестве ротора будет диск (рис. 8.2) и пусть центр масс этого диска не лежит на оси вращения.

Рис. 8.2. Статически неуравновешенный (а) и уравновешенный (б) диски

118

Д – смещение центра масс.

Ускорение смещенного центра масс S диска:

as = ω2 × Д = πn 2 × Д .

30

Сила инерции:

Фи = m × as = m × πn 2 × Д .

30

Эта сила передается на подшипники, фундаментные болты и являет- ся, по сути, возмущающей силой, поскольку ее вертикальная и горизон- тальная составляющие периодически изменяются.

Фих = Фи × cos ϕ

Фиy = Фи × sin ϕ

Возмущающая сила вызывает вибрации, которые в случае резонанса могут приводить к «печальным» последствиям. Чтобы нейтрализовать си- лу инерции Фи , диск нужно уравновесить: на линии ОS с противополож-

ной стороны за точкой О закрепить противовес с массой mпр , который бы создал силу инерции Фи пр , равную по модулю Фи .

Фи пр = −Фи

mпр × (ОЕ) × ω2 = −m × Д × ω2 .

После преобразований получаем:

mпр × (ОЕ) = m × Д .

Т.е. сумма статических масс диска и противовеса должна быть равна нулю. При этом центр О и центр S совпадут в точке О, т.е. в центре этих масс. Иначе говоря, центр масс системы должен лежать на оси вращения.

Условие равенства нулю статических моментов масс должно соблю- даться и в общем случае, когда неуравновешенных масс несколько. Ре- зультирующий вектор их статического момента должен быть равен левой части уравнения (8.3), т.е:

Уравновешивание главного вектора сил инерции называется стати- ческим и для вала (диска) может быть произведено одним противовесом.

119

Если диск статически уравновешен, но перекошен, т.е. его плоскость и ось вращения не перпендикулярны (рис. 8.3), то центры масс полудисков расположатся в разных плоскостях вращения и их силы инерции создадут неурав- новешенную пару с плечом h. Уравновешива- ние пары называется динамическим и может быть произведено противовесами, которые бу- дут создавать пару в плоскости действия ре- зультирующей пары сил инерции.

В общем случае вращающегося вала, ко- гда он несет на себе множество неуравнове- шенных масс, расположенных произвольно с разным дисбалансом, приходится уравнове-

шивать и главный вектор, и главный момент. При этом требуется три про- тивовеса. Один из них (для уравновешивания главного вектора) можно расположить в плоскости действия одного из противовесов для уравнове- шивания главного момента. Складывая силы инерции двух противовесов, установленных в одной плоскости, результирующую этих сил получим од- ним противовесом, закрепленным в точке пересечения составляющих сил инерции. Таким образом, для полного уравновешивания ротора требуется два противовеса. Уравнения для их определения в общем случае имеют следующий вид:

где hi – расстояния неуравновешенных масс относительно плоскости,

где закреплен один противовес.

Полученные уравнения показывают: условием полного уравновеши- вания ротора (вала) является то, что ось вращения будет главной цен- тральной осью инерции.

Уравнения (8.5) решают геометрически, начиная со второго. Опреде-

Решая теперь первое уравнение, находят статический момент второго про- тивовеса. Задав массы второго и первого противовесов тпр1 и тпр2 , нахо-

120