
Механика
.pdf
ГЛАВА 3 |
23 |
|
|
|
|
Убедительного экспериментального доказательства первого следствия нет. Приведём одно из доказательств второго следствия. Положительный μ- мезон рождается в космических лучах одновременно с нейтрино в результате распада π- плюс мезона, а μ- мезон, прожив свою короткую жизнь (~ 10-6 с), распадается на позитрон и два нейтрино (μ+ → e+ + 2ν). Отрезок его жизни можно проследить по треку в пузырьковой камере, с момента когда он в неё попадает до момента, когда из неё выходит, а по длине трека L можно судить о времени его жизни в нашей лабораторной системе К . Можно независимо с помощью имеющихся приборов измерить L и v. Если нет замедления времени, то времена в жизни в К и К’ равны: τ = τ0.
Тогда L = v τ = v τ0 и, таким образом, L и v |
пропорциональны. Если |
|||||
замедление есть, то измеренная длина L |
|
v 0 |
|
|
. Пропорциональ- |
|
|
|
|
|
|
||
1 |
v 2 |
|
||||
|
|
|
|
|||
|
c2 |
|
|
|
||
|
|
|
|
|
|
|
ности в этом случае нет, что и подтверждается измерениями 3. Релятивистский закон сложения скоростей. Пусть ско-
рость некоторой точки относительно К равна u, а относительно K’ равна u’. Запишем преобразования Лоренца (3.3) в дифференциальном виде:
|
|
|
|
|
|
|
|
dt' |
|
vdx' |
' |
|
|||
|
dx' vdt' |
|
|
dy dy' ; dz dz' ; dt |
|
|
|
|
|
||||||
dx |
|
; |
c2 |
||||||||||||
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
|||||||||
|
|
1 |
v 2 |
|
|
|
|
|
1 |
v 2 |
|
|
|||
c2 |
c2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
Имея в виду, что ux = dx/dt лив на дифференциал dt : ux dxdt
иu’x= dx’/dt’ и т.д., получим, поде-
dx' vdt' . Разделив числитель и dt' vdx'
c2
знаменатель на dt’, получим

24 |
|
|
|
|
|
|
|
|
|
|
|
ЧАСТЬ 1. МЕХАНИКА |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v 2 |
|
|
|
|
v 2 |
|
|
|
||||
|
|
u' x v |
|
u' y |
1 |
|
|
|
|
u'z |
1 |
|
|
|
|
|
|||
|
|
|
c2 |
c2 |
|
|
|
||||||||||||
ux |
|
|
|
и далее uy |
|
|
|
|
|
|
; uz |
|
|
|
|
|
. |
||
1 |
vu' x |
|
1 |
vu' x |
|
|
|
1 |
vu' x |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
c2 |
|
|
c2 |
|
|
|
c2 |
|
|
|
|||||||
Последние соотношения выражают релятивистский закон сложения скоростей. Если в них заменить плюс на минус, а штрихованные и нештрихованные компоненты поменять местами, получатся выражения для u’x, u’y, u’z через ux, uy, uz .
Видно, что в отличие от классического галилеевского закона сложения скоростей компоненты uy и uz по направлениям y и z, вдоль которых система K’ не движется, также претерпевают преобразования и зависят от скорости движения v системы K’ вдоль Х. При v c получим классический закон сложения скоростей, а при v = c получим, что также и в K будет ux = c. Иначе и быть не могло, т.к. преобразования Лоренца выводились исходя из предположения инвариантности скорости света. Однако длина стержня и временной интервал инвариантами уже не являются.
Обобщением специальной теории относительности является общая теория относительности, рассматривающая также ускоренное движение и поведение частиц и излучения в гравитационном поле.
ГЛАВА 4 |
25 |
|
|
|
|
ГЛАВА 4. ОСНОВНЫЕ ПОНЯТИЯ ДИНАМИКИ. ЗАКОНЫ
ДИНАМИКИ. МОМЕНТ ИМПУЛЬСА И МОМЕНТ ИНЕРЦИИ. ВИДЫ ДВИЖЕНИЯ
В отличие от кинематики динамика анализирует движение вместе с причинами, вызывающими это движение и изменения в нём. А начало любого движения и его изменения связаны с взаимодействием между телами. Количественной мерой взаимодействия между телами является сила (по-гречески сила – δυναμας; отсюда и динамика). Сила – векторная величина. Причём взаимодействие может быть непосредственное и на расстоянии – посредством силового поля, т.е. области пространства, в котором обнаруживается действие силы. Законы динамики были сформулированы английским физиком Исааком Ньютоном и носят его имя. Справедливы они, как уже говорилось, при v c. Будем в дальнейшем считать, что именно с такими малыми скоростями мы и имеем дело (если не будут оговорены иные условия).
Мы уже вводили понятие инерции (глава 1) как свойства всех материальных тел сохранять состояние покоя или равномерного прямолинейного движения, если не действуют внешние силы. Коли-
чественной мерой инертности тел является масса. В СИ масса из-
меряется в килограммах (кг). В бюро мер и весов в Севре под Парижем хранится эталон 1 кг – последний оставшийся из рукотворных метрологических эталонов. Остальные уже были заменены естественными. Масса – величина скалярная и обладает свойством аддитивности, т.е. масса тела складывается из масс отдельных его частей или вычитается, если из тела удаляется какая-либо его

26 ЧАСТЬ 1. МЕХАНИКА
часть. Как показали эксперименты на ускорителях, масса зависит от скорости по закону m m0 / 
 1 (v 2 / c2 ) и ведёт себя как величина γ (рис. 3.3). Она при v = 0 равна m0 и называется массой покоя и быстро возрастает при увеличении скорости свыше 70-80% от с.
1 (v 2 / c2 ) и ведёт себя как величина γ (рис. 3.3). Она при v = 0 равна m0 и называется массой покоя и быстро возрастает при увеличении скорости свыше 70-80% от с.
Основным законом динамики является второй закон Ньютона: ускорение, с которым движется тело, прямо пропорционально дей-
ствующей силе и обратно пропорционально массе: a mF . Если
действует не одна, а несколько сил, то под F понимается их векторная сумма. Единица силы [F ] = кг·м / с2 – ньютон (Н).
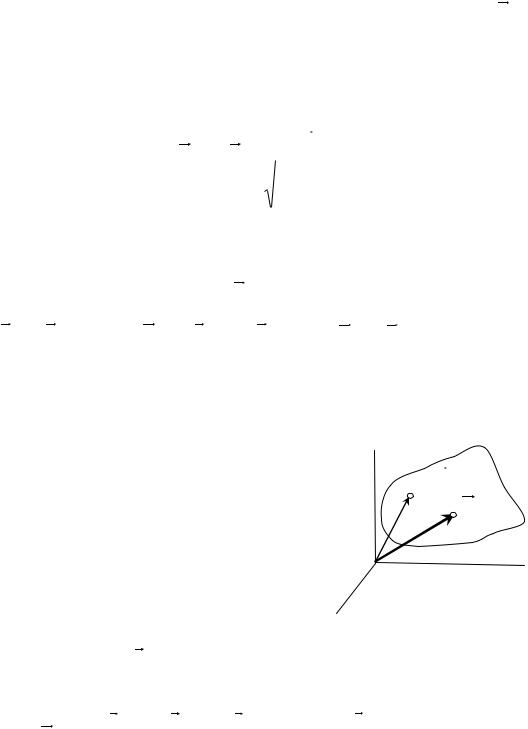
Третий закон Ньютона: действия двух тел друг на друга равны по величине и противоположны по направлению: F 12 F 21 . Здесь F 12 - сила действующая на первое тело со стороны второго, а F 21 - сила действующая на второе тело со стороны первого. Если на столе 1 лежит кирпич 2 (рис. 4.1), то величина силы F 12 , с которой кирпич 2 действует на стол 1 равна величине силы F 21 , с которой стол 1 действует на кирпич 2 . Поскольку силы приложены к разным телам, то нельзя искать их равнодействующую! Третий закон не позволяет также определить величину этих сил. Для кирпича на
столе можно написать F12 F21 mg . |
|
F21 |
|
Однако здесь мы уже применили второй за- |
|
кон Ньютона, зная из опытов Галилея по свобод- |
2 |
ному падению, что ускорение, обусловленное при- |
1 |
|
|
тяжением Земли одинаково для всех тел и равно g |
|
= 9,8 м/с2. Этот результат, равно как все законы |
F12 |
|
Рис. 4.1 |
||
|
||
Ньютона и многие другие фундаментальные зако- |
|
ны физики, ниоткуда не выводится, а является обобщением человеческого опыта.
ГЛАВА 4 |
27 |
|
|
|
|
Сила, с которой тело действует на подставку (или подвес) называется весом тела. В нашем примере весом является сила F 12 .
Единицей силы в СИ является ньютон: [F]= [m][a] = кг·м/с2 = Н. Другой динамической характеристикой – мерой запаса коли-
чества движения – является импульс, определяемый как
p mv |
|
m0 v |
|
|
. |
|
|
|
|
|
|
||
1 |
v 2 |
|
||||
|
|
|
|
|||
|
c2 |
|
|
|
||
|
|
|
|
|
|
|
Как сила или любая другая векторная величина, импульс складывается по законам векторной алгебры и полный импульс системы материальных точек равен p pi . Его размерность: кг·м/с.
|
i |
|
Так как a dv / dt , то |
F ma mdv / dt |
и F d p / dt . Последняя |
форма второго закона справедлива и для релятивистского случая и является более универсальной.
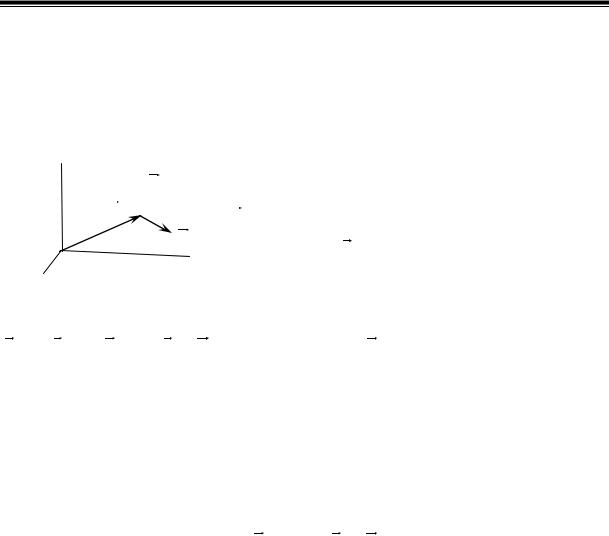
Центр инерции. Пусть имеется твёр- |
|
|
дое тело, которое можно представить как |
mi , r i |
|
совокупность большого числа материаль- |
||
R0 |
||
|
||
ных точек (рис. 4.2), между которыми ничего |
|
|
нет (модель типа «гречневая каша». Опре- |
|
|
делим теперь центр инерции как точку ради- |
|
|
ус-вектор которой (рис. 4.2) определяется |
Рис. 4.2 |
|
через радиус-векторы r i точек тела по фор- |
|
муле |
|
|
|
|
|
|
|
|
|
|
|
R0 |
|
m1r 1 m2 r |
2 m3 r 3 ... |
|
mi |
r i |
. |
(4.1) |
|||
m1 |
m2 |
m3 ... |
|
mi |
|||||||
|
|
|
|
|
|||||||
В других случаях вещество распределено непрерывно (модель типа «манная каша»), и тело в виде совокупности материальных точек представить нельзя. Тогда вместо массы mi рассматрива-

28 ЧАСТЬ 1. МЕХАНИКА
ется элементарная масса dm = ρ dV. |
Вместо суммы будет интеграл |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r dV |
|
|
по всему объёму V. Формула (4.1) принимает вид R0 |
|
V |
. Про- |
||||||||||||||
dV |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
dR0 |
|
|
|
|
|
|
1 |
|
d r i |
|
P |
|
|
|
||
изводная v 0 |
|
d |
mi r i |
|
mi |
|
, где М |
- пол- |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
dt |
|
dt |
mi |
|
M |
|
dt |
|
M |
|
|
|
||||
ная масса, а Р - полный импульс тела, является скоростью центра инерции. Таким образом, P MV 0 . Это означает, что, не зная импульсов pi всех отдельных элементов системы, но, зная массу всей системы и скорость её центра инерции. Можно определить полный импульс. Центр инерции является центром средоточения массы всей системы.
Поступательное и вращательное движение твёрдого тела. Число степеней свободы.
Поступательное движение – такое, при котором все точки тела движутся по одинаковым траекториям. Скорости всех точек при этом в любой момент одинаковы, а прямая, соединяющая две любые точки тела, движется параллельно самой себе. (Например, движение стеклоочистителей автобуса «Икарус», движение ящика стола и т.п.).
Вращательное движение бывает простое и сложное. Простое
– это вращение тела вокруг фиксированной оси; при этом все точки тела описывают окружности, лежащие в параллельных плоскостях. Сложное – когда тело вращается вокруг фиксированной точки. В первом случае достаточно ввести одну координату φ(t), отсчитываемую от какого-нибудь начального положения, чтобы охарактеризовать положение тела в любой момент времени. Во втором случае нужно ввести три таких координаты: φ(t), χ(t), ψ(t) – углы Эйлера
ГЛАВА 4 |
29 |
|
|
|
|
углы Эйлера, характеризующие поворот тела вокруг любой из трёх взаимно перпендикулярных осей. Любое сколь угодно произвольное движение твёрдого тела можно представить как сумму поступательных и вращательных движений.
Количество i независимых координат, вполне определяющих положение тела либо количество перемещений, совершаемых телом одновременно и независимо друг от друга, называется числом степеней свободы. Так, для простого вращательного движения i =1, а для сложного i =3 . Свободное движение материальной точки описывается тройкой координат x, y, z. Поэтому i =3. При движении точки по плоскости i =2, а при движении маленькой бусинки вдоль нити i=1. Любое движение материальной точки (включая движение по окружности) – поступательное. Вращательное движение – атрибут твёрдого тела, системы материальных точек. Две материальные точки, соединённые жёстким невесомым стержнем длиной L, образуют так называемую гантель. Это упрощённая модель многих двухатомных молекул. Гантель имеет три поступательных степеней свободы и две вращательных. Отсутствует вращение материальной точки вокруг самой себя. Арифметика подсчёта степеней свободы проста. В гантели каждая точка при отсутствии связи имела бы три степени свободы; итого шесть. Одну из координат всегда можно выразить через другую из соотношения
L2 ( x2 x1 )2 ( y2 y1 )2 ( z2 z1 )2 ,
и таким образом на одну степень свободы становится меньше. В общем случае при наличии k независимых жёстких связей число степеней свободы в системе из N материальных точек i =3N – k. Чтобы жёстко закрепить твёрдое тело, достаточно взять три точки, не лежащие на одной оси, связанные тремя жёсткими связями.
30 ЧАСТЬ 1. МЕХАНИКА
Поэтому i= 3N – k = 3 ×3 – 3 = 6, т.е. три поступательных и
три вращательных степеней свободы. |
|
|
||
Момент импульса и момент инерции. |
Пусть имеется материальная |
|||
|
точка mi , движущаяся относительно нача- |
|||
Li |
ла |
О системы координат со |
скоростью |
|
r i |
v i |
(рис. 4.3). Её положение задаётся ради- |
||
|
||||
v i |
ус-вектором r i . (Оба вектора в плоскости |
|||
|
||||
Рис. 4.3 |
чертежа). |
Моментом импульса точки |
||
|
|
|
|
|
|
называется |
векторная |
величина |
|
Li [ r i mv i ] [ r i pi |
]. Направление Li определяется правилом |
|||
буравчика (см. гл. 2): «от нас» для случая, изображённого на рисунке; если «к нам», то будем изображать это направление точкой в кружочке – острие летящей к нам стрелы; если «от нас», то крестиком в кружочке – оперение стрелы, летящей от нас. Если речь идёт о твёрдом теле, то его момент импульса равен векторной сумме моментов отдельных точек Li [ r i pi ]. Размерность момента импульса [ L ] = кг·м2 / с.
Рассмотрим теперь простое вращательное движение твёрдого тела вокруг фиксированной оси (рис. 2.5). Пусть тело представляет собой совокупность материальных точек mi , а ri - расстояние i – й точки до оси вращения. Моментом инерции тела относительно фиксированной оси называют величину J = mi ri2 . Если же масса
распределена непрерывно, то J r 2 dV . Здесь ρ dV = dm – эле-
V
ментарная масса, r – расстояние от dm до оси вращени, V - объём всего тела. Размерность момента инерции [J ] = кг · м2. Как и масса, эта величина аддитивна. Она является мерой инертности по отно-
ГЛАВА 4 |
31 |
|
|
|
|
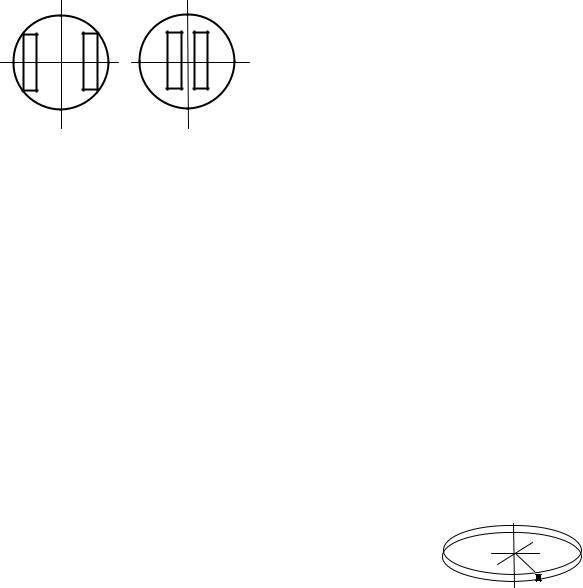
шению к вращательному движению (а масса по отношению к поступательному). Простой эксперимент показывает, что эта мера инертности различна при равных массах. Если у вершины наклонной
плоскости удержать два цилиндра (рис. 4.4) равной массы, но имеющих разный момент инерции (Jправ < Jлев) вследствие различной ориентации внутренних сухариков, а затем одновременно освободить цилиндры, то время скатывания будет различным (левый скатится быстрее).
Вычисление моментов инерции тел является важной инженерной задачей при проектировании механизмов с вращающимися узлами. Правильный расчёт моментов инерции уменьшает биения, обеспечивает устойчивое вращение и увеличивает срок службы подшипников. Приведём примеры расчёта моментов инерции.
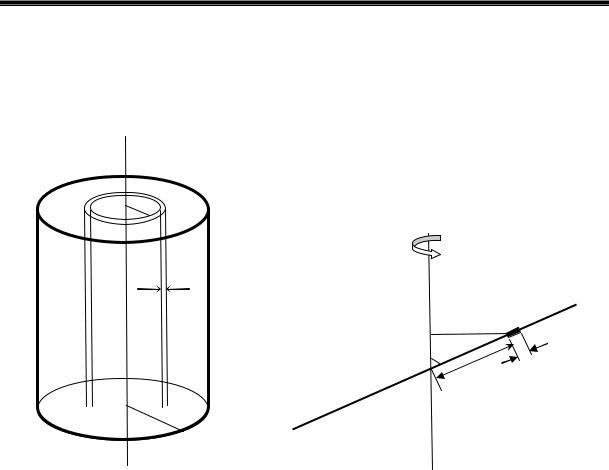
1.Тонкий обруч массой М и радиусом R
или тонкостенный цилиндр (рис. 4.5). В этом случае любой элемент массы находится на одинаковом расстоянии R от оси вращения. Его момент
инерции dJ = R2dm. Момент инерции всего обруча относительно оси, проходящей через центр равен J = R2 ∫ dm = MR2.
2. Cплошной диск массой М и радиусом R или сплошной цилиндр (рис. 4.6) относительно оси симметрии. Выделим в сплошном цилиндре цилиндр тонкостенный радиуса r с толщиной стенки равной dr. Его масса будет dm = ρ dV (где ρ - плотность), а элемент объёма dV из-за малой толщины стенки цилиндра можно представить как произведение площади его развёртки на толщину:
32 ЧАСТЬ 1. МЕХАНИКА
dV = 2πr·h·dr. По определению ρ = M / V = M / (πR2h). Поэтому, учитывая результат примера 1, получим
dJ
h
|
|
M |
|
2M |
R |
2M r |
4 |
|
R |
MR |
2 |
|
||||
|
|
|
|
|
||||||||||||
r 2dm r 2 dV r 2 |
2 rhdr; J |
r 3dr |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
R2h |
|
R2 |
0 |
|
R2 4 |
|
0 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Тонкий однородный стержень |
|||||||||||||
|
|
массой М и длиной L , образующий угол |
||||||||||||||
r |
|
θ относительно оси, проходящий через |
||||||||||||||
|
|
|||||||||||||||
|
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
dm |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ
x
 R
R
Рис. 4.6 |
Рис. 4.7 |
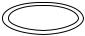
центр инерции стержня (рис. 4.7).
Выделим элементарную массу dm длиной dx, находящуюся на расстоянии х от центра стержня и на расстоянии r от оси вращения. Тогда dm = ρ dх, где ρ - линейная плотность, равная M / L. Поскольку r / x = sin θ , то dJ = x2(M / L)sin2 θ dx и полный момент инерции получится интегрированием по всей длине стержня от –L/2 до +L/2 или интегрированием по половине стержня и умножением результата на два:
|
|
|
|
L / 2 |
|
|
|
|
|
3 |
|
L / 2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
J 2 |
M |
sin2 |
|
|
x 2dx 2 |
M |
sin2 |
|
x |
|
|
|
|
|
ML |
sin2 . |
|
|
|
|
|
|
|
|
|||||||||
|
L |
|
0 |
|
L |
3 |
|
|
0 |
|
12 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Тело вращения, получаемое вращением какой-либо функции y(x) вокруг оси X и имеющее форму вазы, бочки или любого гончарного изделия или изделия, изготовленного на токарном
