
Механика
.pdf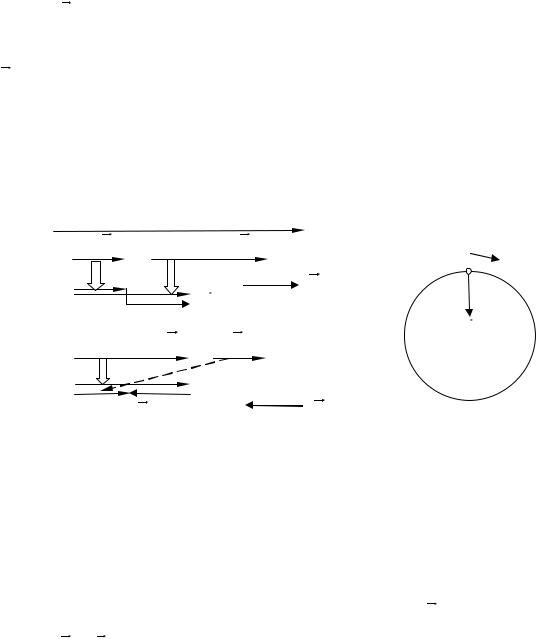
ГЛАВА 2 |
13 |
|
|
|
|
торых a (тангенциальное ускорение) направлена вдоль касательной и характеризует изменение скорости по величине, а другая аn (нормальное или центростремительное ускорение) по перпендикулярному к касательной направлению – к центру кривизны траектории в данной точке – и характеризует изменение по направлению (рис. 2.1 б). Рассмотрим важные частные случаи, часто повторяющиеся в инженерной практике.
а) |
v t |
v t t |
X |
|
|
v= const |
|
v |
а |
|
|
|
|
|
v t |
v t t |
в) |
а |
|
|||
|
|
||
б) |
|
|
|
v |
|
а |
|
Рис. 2.2. Убыстренное (а) и замедленное (б) прямолинейное движение вдоль оси Х. Равномерное движение по окружности (в)
1. Точка движется прямолинейно. В этом случае нет изменения по направлению. Нормальное ускорение аn = 0. Полное ускорение a = a и направлено либо в сторону движения (убыстрение, рис. 2.2 а ), либо против движения (замедление, рис. 2.2 б ). Если в качестве положительного направления оси Х выбрать направление движения, то в первом случае ускорение положительно, а во втором отрицательно. Если в качестве положительного направления выбрать направление противоположное движению, то поменяются и знаки ускорений. Поэтому неверно расхожее мнение, что убыстре-
14 ЧАСТЬ 1. МЕХАНИКА
ние – это положительное ускорение, а замедление – отрицательное. Всё зависит от того, как выбрать положительное направление оси Х.
2. Точка движется по окружности с постоянной по величине скоростью (v = const). Здесь скорость меняется только по направлению. Поэтому a = 0, полное ускорение a = аn и направлено к центру окружности (рис. 2.2 в ). Строго говоря, любое криволинейное движение является ускоренным. Однако во многих практических случаях, например, рассматривая движение автомобиля по извилистой дороге с постоянной скоростью, этим обстоятельством пренебрегают.
Рассмотрим частицу, движущуюся по любой криволинейной траектории. Для простоты рассмотрим движение в плоскости XOY,
хотя это и не принципиально. |
|
|||
Y |
C |
|
а |
|
|
R |
|||
|
|
|||
|
d |
|
|
|
|
|
R |
|
|
|
|
an |
a |
|
|
|
|
||
en |
|
ds |
|
j |
e |
|
|
A |
|
i |
X |
Рис. |
2.3 |
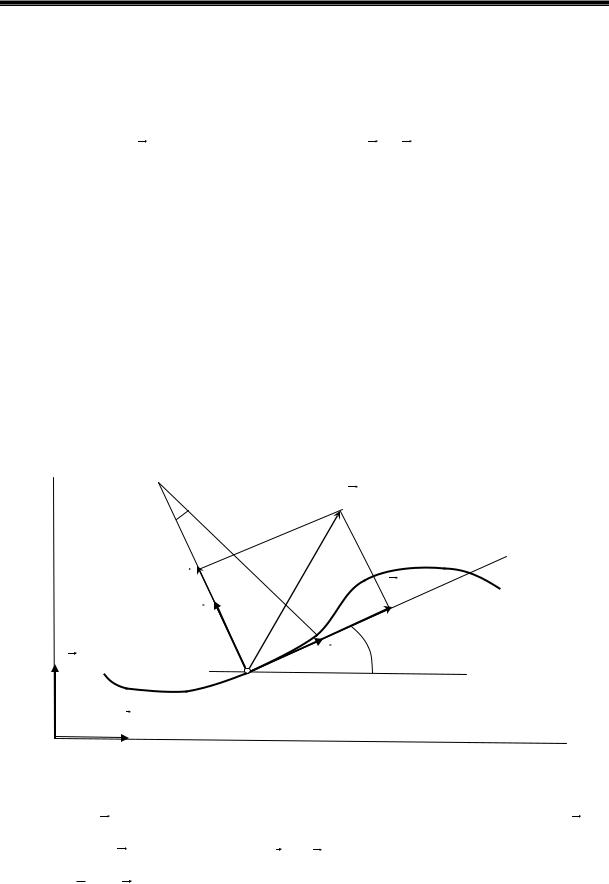
Пусть в момент t частица находится в точке А и имеет полное ускорение а (рис. 2. 3), которое разложим на тангенциальное a и нормальное an . Введём орты i и j и вспомогательные единичные векторые и еn вдоль касательно в точке А и в перпендикулярном

ГЛАВА 2 |
15 |
|
|
|
|
направлении соответственно. Тогда скорость |
v v e , а полное |
ускорение равно |
|
a dtd v e dvdt e v ddte .
Представим векторы e и еn как разложения по ортам i учитывая, что по величине и направлению они не изменяются:
e 1 cos i 1 sin j ;
(2.2)
и j ,
en 1 cos( 90 ) i 1 sin( 90 ) j sin i cos j .
Поэтому
|
|
|
i sin |
d |
j cos |
d |
|
d |
. |
|
de |
en |
(2.3) |
||||||||
dt |
dt |
dt |
|
|||||||
|
|
|
dt |
|
||||||
Найдём dφ/dt. Для этого рассмотрим бесконечно малый сектор со сторонами R и углом dφ, ограниченный дугой ds. Так как по определению радианной меры ds/ R = dφ, то dφ/ds = 1/R. Таким об-
разом, d d ds d v 1 v . Подставляя этот результат в (2.3), dt ds dt ds R
а (2.3) в (2.2), получим окончательные выражения для вектора полного ускорения, его абсолютной величины и компонент:
|
dv |
|
v 2 |
|
|
|
dv 2 |
v 2 |
2 |
|
|
dv |
|
|
v 2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
a e |
|
en |
|
; a |
a |
|
|
|
|
|
|
|
; a |
|
|
|
; an |
|
|
. (2.4) |
|
|
|
|
|
|
|
||||||||||||||
|
dt |
|
R |
|
|
|
dt |
R |
|
|
|
dt |
|
|
R |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
Равноускоренное |
движение |
имеет |
место, |
когда |
а соnst . |
|||||||||||||||
Это возможно в следующих случаях.
1.Прямолинейное движение ( а соnst , аn 0 ).
2.Криволинейное движение с траекторным способом описания, когда нормальным ускорением пренебрегают.
3.Криволинейное движение под действием постоянной силы.
Для случаев 1 и 2 можно положить an = 0. Тогда a = dv/dt и v = adt v0 at , где v0 - постоянная интегрирования.
16 |
|
|
|
|
ЧАСТЬ 1. МЕХАНИКА |
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
При t = 0 |
имеем v v0 , и следовательно v0 |
является началь- |
||||||
ной скоростью. |
Поскольку |
v |
ds |
, то |
s vdt v |
0t |
at 2 |
s0 . Кон- |
|
|
|||||||
|
|
|
dt |
|
|
2 |
|
|
станта определяется выбором начала отсчёта траектории (Расстояние от Москвы можно отсчитывать от Кремля, а можно от кольцевой дороги). Обычно её полагают равной нулю, считая, что расстояние отсчитывается от начала движения. В векторной форме можно за-
писать: |
v v |
|
at; R v 0t |
at 2 |
s0 , где s |
|
- вектор, проведённый |
0 |
|
0 |
2
из начала координат в точку начала движения.
Рассмотрим теперь случай 3. Камень, брошенный под углом к горизонту, находится в поле тяжести Земли и движется с полным ускорением g , направленным вниз (рис. 2.4). Это тоже равноускоренное движение, поскольку в
Y |
|
a an |
g |
|
|
|
любой точке g const . |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Угловая скорость и угло- |
|
|
|
|
|
|
|
|
|
a |
|
an |
|
|
|
|
|
вое ускорение. Рассмотрим точ- |
|
|
|
|
a |
|
|
||
|
|
g |
|
|
|
ку М, принадлежащую некото- |
||
|
|
|
an |
|
Х |
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|||
|
g |
|
g |
|
|
рому телу, вращающемуся от- |
||
|
|
|
|
|
||||
|
|
|
|
|
|
|
||
|
|
Рис. 2.4 |
|
|
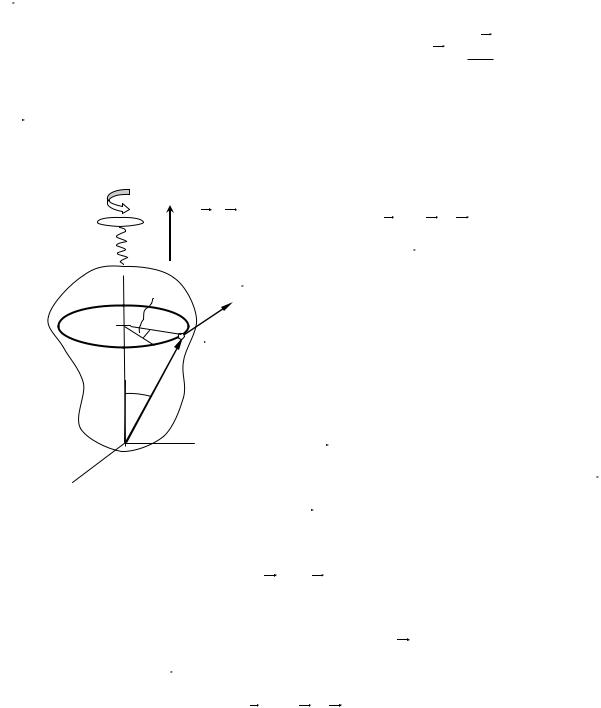
носительно оси ОО’ (рис. 2.5). |
|||
|
|
|
|
|
|
|
|
Аналогично вектору линейного |
перемещения введём |
формально вектор углового перемещения |
|||||||
d , направление которого определим правилом буравчика: при вращении рукоятки буравчика в направлении вращения тела направление движения его винта укажет направление вектора d . Наглядного смысла во введении такого вектора нет. Однако, как увидим в дальнейшем, при таком формальном определении этого вектора другие более «осязаемые» величины будут иметь величину и направление, соответствующие физической реальности. Выберем
ГЛАВА 2 |
17 |
|
|
|
|
начало декартовых координат где-нибудь на оси вращения и соединим его с мгновенным положением точки М радиус-вектором R .Определим далее мгновенную угловую скорость как быстроту
изменения углового перемещения во времени: ddt . Она изме-
ряется в радианах в секунду [ω] = рад/с или с-1 и направлена, как и d - вверх вдоль оси. Линейная скорость v = ds|dt = r dφ |dt = ω r.
Так как r = R sin α, то последнему соотношению можно придать векторную форму
|
d , |
|
v [ R ] . |
(2.5) |
|
|
|
||
|
|
Вектор v , как и любой другой, |
||
O' |
dφ |
определяемый векторным произве- |
||
|
v |
|||
r |
М |
дением, |
направлен по правилу бу- |
|
R |
|
|
|
|
|
равчика: |
вращаем его |
рукоятку в |
|
|
|
|||
|
плоскости векторов кратчайшим по- |
|||
|
|
|||
O |
|
воротом от первого ко второму. То- |
||
|
|
|
|
|
|
|
гда v будет направлен перпендику- |
||
|
|
лярно плоскости, в которой лежат |
||
Рис. 2.5 |
|
и R , по касательной к траектории и |
||
|
|
|||
|
|
в сторону движения точки. Угловое |
||
ускорение определяется как d / dt ; |
размерность [β ] = рад/с2 |
|||||||||
или с-2 . При вращении тела вокруг фиксированной оси ω |
изменяет- |
|||||||||
ся только по величине |
и направлено вдоль при убыстрении вра- |
|||||||||
щения и против |
- |
при замедлении. |
Линейное тангенциальное |
|||||||
ускорение |
в этом |
|
случае a [ R ] . |
При β = const |
получим |
|||||
|
0 |
t |
и |
t t 2 / 2 |
0 |
. |
|
|
||
|
|
0 |
|
|
|
|
|
|
||
18 |
ЧАСТЬ 1. МЕХАНИКА |
|
|
|
|
ГЛАВА 3. КИНЕМАТИКА СПЕЦИАЛЬНОЙ ТЕОРИИ
ОТНОСИТЕЛЬНОСТИ. СЛЕДСТВИЯ ИЗ ПРЕОБРАЗОВАНИЙ ЛОРЕНЦА
По Галилею для инерциальных систем отсчёта (ИСО) К и К’ (рис. 1.3) связь компонент cкоростей u ↔ u ’ для некоторой материальной точки, например мухи в корабле, который движется вдоль берега со скоростью v так, что х параллельно х‘ получится диффе-
ренцированием формул (1.1): |
u |
|
|
dx' |
v |
и т.д. Искомые соотно- |
|||||||||
x |
dt |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
и |
|
ux |
|
|
|
uy |
|
uz |
||
шения ux ux |
v ; uy uy ; uz |
uz |
ux |
v; uy |
; uz |
||||||||||
называются классическим законом сложения скоростей. |
|
|
|
|
|||||||||||
В конце XIX века ряд экспериментов |
|
К |
|
|
|
|
c |
||||||||
|
|
|
|
|
|||||||||||
(например, опыты Майкельсона – Морли, см. |
|
|
|
|
v |
||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
[1 ]) поставил |
под сомнение |
классический |
|
Рис. 3.1 |
|
|
|||||||||
закон сложения скоростей. Возникли пред- |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|||||||||
положения, что скорость света в вакууме является инвариантом для инерциальных систем и не зависит от скорости их движения. Так, если на тележке (рис. 3.1), движущейся относительно неподвижной
К’ v |
O’ |
системы К со скоростью v , установлен фо- |
||
|
|
нарик, то скорость посылаемого им излуче- |
||
|
|
|
||
К |
|
ния будет с и относительно тележки, и от- |
||
C |
O C’ |
|||
носительно системы К . А не v + c ! То что |
||||
|
|
|
||
|
K’ |
|
скорость света не зависит от скорости дви- |
|
|
D |
O’ D’ |
||
|
жения источника, противоречит принципу |
|||
|
Рис. 3.2 |
|||
|
|
|||
|
|
|
относительности Галилея. Пусть в точке О |
|
системы К |
(рис. 3.2) возникает вспышка света. Через некоторое |
|||
время волновой фронт достигнет точек С и С’, которые находятся на
ГЛАВА 3 |
19 |
|
|
|
|
одинаковых расстояниях от О. Для системы К’, движущейся вдоль Х со скоростью v так, что в момент t = t’ = 0 начала обеих систем совпадают, свет в точку D’ придёт раньше, чем в D. Следовательно, события, одновременные в К , не являются таковыми в К’ . Поэтому одновременность относительна, и часы в К и в K’ не синхронны! Выход был предложен А. Эйнштейном в 1905 г. в его специальной теории относительности, которая базируется на двух постулатах (т.е. аксиомах – положениях, принимаемых на веру без доказательств):
Все инерциальные системы равноправны, и все физические явления и процессы протекают в них одинаковым образом;
Скорость света в вакууме одинакова во всех ИСО, не зависит от скорости движения источника и является предельной скоростью распространения взаимодействий.
Как видим, первый является принципом относительности Галилея, а второй – обобщением опытных данных, полученных исследователями XIX века.
Пусть имеются две ИСО К и К’ . Последняя движется так, что X’ скользит вдоль Х (см. рис. 1.3). В момент t = t’ = 0 начала обеих систем совпадают. В этот момент в О возникает вспышка света. Через t секунд в К волновой фронт распространится в виде сферы радиуса c t . Аналогично в K’ свет достигнет точек сферы радиуса
c t’ . Таким образом, для К и K’ |
получим соответственно: |
|
x 2 y 2 z2 c2t 2 ; |
x 2 y 2 z 2 c2t 2 . |
(3.1) |
Из опыта известно, что пространство однородно (при переходе от одной его точки к другой свойства его характеристик остаются неизменными) и изотропно (его свойства одинаковы по различным направлениям). Про время известно, что оно однородно:

20 ЧАСТЬ 1. МЕХАНИКА
развитие и изменение данного физического явления не зависит от того, в какой момент времени данная ситуация сложилась. Так, процесс развития цыплёнка из яйца происходил одинаково при Петре I и при современном правительстве. Математически эти свойства
означают линейную связь координат и времени: |
|
|
||
x = γ(x’+vt’); |
y = y’; |
z = z’; |
t = at’ + bx’. |
(3.2) |
При этом если |
v c , эти соотношения должны переходить в |
|||
преобразования Галилея (1.1), т.е. должно быть: γ, а →1 и b →0. Определим γ, и b. Для этого подставим (3.2) в (3.1). Получим:
γ 2(x’+vt’)2 + y2 + z2 = c2(at’ + bx’)2 ;
γ2x2 + 2 γ2vx’t’ + γ2v2t’2 + y’2 + z’2 = c2a2t’2 + 2c2abt’x’ + c2b2x2 и 2x’t’(γ2v - c2ab) + (γ2 - c2b2)x’2 + y’2 + z’2 = (c2a2 - γ2v2)t’’2 .
Сравним последнее соотношение со второй формулой из (3.1), которая удовлетворится, если 2x’t’(γ2v - c2ab) = 0; (γ2 - c2b2) = 1 и (c2a2 - γ2v2) = с2. Эти три уравнения образуют систему. Первое из них даёт b = γ2v/(c2a). Подставляя b во второе уравнение, получим
γ2 |
– [γ4v2/ |
(c2a2)] = |
1, |
|
а |
из |
|
третьего |
|
|
уравнения |
получим |
||||||||||||
v2 |
= (c2a2 - |
c2)/ |
γ 2 . |
Из |
двух |
последних |
соотношений |
получим |
||||||||||||||||
γ2 |
– γ2(c2a2 - c2) / |
(c2a2) = 1 , откуда γ = а. Подстановка γ = а в третье |
||||||||||||||||||||||
уравнение системы даст γ2(c2 - v2) = c2, откуда |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v |
|
|||||
|
|
|
|
c |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ = |
|
|
|
|
|
|
|
|
; b |
|
|
|
c2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
c2 v 2 |
|
1 |
v 2 |
|
1 |
v 2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|||||||
Подставляя найденные коэффициенты линейной связи в (3.2), получим преобразования специальной теории относительности, открытые Лоренцом и носящие его имя:

ГЛАВА 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t' |
vx' |
|
|
|
|||||||||||||
|
|
x' vt' |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x |
|
|
|
; y y' ; z z' ; t |
|
c2 |
; |
|
γ |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
1 |
v 2 |
|
|
|
|
|
|
|
1 |
v 2 |
|
|
|
|
|
|
||||||||||||
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
2 |
|
|
|
|
|
(3.3) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vx |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x vt |
|
|
|
|
|
|
|
|
. |
|
1 |
|
|||||||||||||||||
x' |
|
|
; y' y ; z' z; t' |
|
|
c2 |
|
v/c |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
1 |
v 2 |
|
|
|
|
|
|
|
1 |
v 2 |
|
0 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||||
|
|
|
c2 |
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.3 |
|
|
|
|
Нетрудно видеть, |
что при v c |
они переходят в преобразо- |
||||||||||||||||||||||||
вания Галилея. На рис. 3.3 показана зависимость γ от v/c, из которой видно, что отход от классической физики к релятивистской (описываемой теорией относительности) наступает при скоростях порядка 70-80% от скорости света. Затем даже незначительное увеличение скорости приводит к сильному изменению γ , т.е. к ярко выраженным релятивистским эффектам.
Следствия из преобразований Лоренца Будем рассматривать ИСО К’ , движущуюся в направлении Х
со скоростью v так, то Х’ скользит вдоль Х.
1. Сокращение длины движущегося стержня. Пусть в К’ по-
коится стержень, расположенный параллельно Х’. Его длина, измеренная в той системе, где он покоится (т.е. в K’), называется собственной длиной L0, величина которой L0 = х2’ – x1’, где х2’ , x1’ - координаты конца и начала стержня в K’. Для того, чтобы измерить
|
К’ |
|
|
|
|
длину стержня в К, необходимо в один и |
|
К |
|
|
|
|
|
||
|
|
v |
|
|
|
тот же фиксированный момент t0 по ча- |
|
|
x’1 |
x’2 |
|
||||
|
|
|
сам в К отметить координаты х2 и х1 кон- |
||||
|
|
|
|
|
|
X’ |
|
|
|
|
|
|
|
||
|
|
|
|
X |
|||
|
|
|
|
ца и начала стержня. Пользуясь форму- |
|||
|
|
|
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Рис. 3.4 |
|
|
|
|
лами (3.3), получим: |
||
|
|
|
|
|
|
|
|
22 ЧАСТЬ 1. МЕХАНИКА
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L x' |
|
x' |
|
|
x |
2 |
vt |
0 |
|
|
x |
1 |
vt |
0 |
|
|
x |
2 |
x |
1 |
|
|
|
|
L |
|
|
|
и L L 1 |
|
v |
2 |
. |
|||||||||||
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
0 |
|
|
|
|
|
v |
2 |
|
|
|
|
|
|
v |
2 |
|
|
|
|
|
|
|
v |
2 |
|
|
|
|
|
v |
2 |
0 |
|
|
c |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
c2 |
|
|
|
c2 |
|
|
c2 |
|
|
|
c2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Таким образом, L< L0, что означает, что длина стержня, измеренная в ИСО К, уменьшилась (!!!)
2. Замедление хода движущихся часов. Пусть часы в K’
покоятся. Пусть далее в некоторой точке x’0 системы K’ произошло развитие какого-либо события, начавшегося в момент t’1 , и закончившегося в момент t’2. Например, в момент t’1 космонавт закурил сигарету, а в момент t’2 бросил окурок в урну. Длительность события τ0 = t’2 - t’1 , измеренная в K’, где часы покоятся, называется собственным временем события. Соответствующий интервал в К будет
|
|
|
|
|
t' |
2 |
vx'0 |
|
|
t' |
1 |
vx'0 |
|
|
|
|
t'1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t'2 |
|
|
|
|
|
|
|
|
|
|
|
v |
2 |
|
|
||||||||||||
τ = t |
|
t |
|
|
c2 |
|
c |
2 |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
1 |
. |
||||||||||||||||||||||
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
c |
2 |
|||||||||||
|
|
|
v |
2 |
|
|
|
|
|
v |
2 |
|
|
|
|
|
v |
2 |
|
|
v |
2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
c2 |
|
|
|
c2 |
|
|
c2 |
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Поэтому τ0< τ, т.е. движущиеся часы идут медленнее (!!!)
Космонавт, улетевший на ракете, движущейся прямолинейно с релятивистской скоростью, станет моложе своих бывших ровесников, с которыми он может регулярно общаться с помощью средств телекоммуникаций.
С этим следствием связан парадокс близнецов. Жили-были близнецы А и Б (например, Алик и Боря). Боря, собираясь улететь в космос на быстрой ракете, говорит Алику: «Вследствие второго следствия по возвращении из космоса я окажусь моложе тебя». Алик возражает: «По первому постулату Эйнштейна все ИСО равноправны и можно считать, что это ты на своей ракете останешься в состоянии покоя, а я буду относительно тебя двигаться с такой же скоростью в противоположном направлении, и по возвращении моложе буду я». Парадокс основан на том, что повторная встреча близнецов возможна только при развороте ракеты и при последующем включении тормозов. А это означает выход из инерциальных систем отсчёта, для которых справедлива специальная теория относительности. Анализ ситуации с учётом ускоренного движения показал, что прав всё-таки Борис.
