Оценка качества построенной модели регрессии

Качество модели регрессии – адекватность построенной модели исходным (наблюдаемым) данным.

Чтобы измерить тесноту связи, т.е. измерить, насколько она близка к функциональной, нужно определить дисперсию, измеряющую отклонения у от у_х и характеризующую остаточную вариацию, обусловленную прочими факторами. Они лежат в основе показателей, характеризующих качество модели регрессии.

Качество парной регрессии определяется с помощью коэффициентов, характеризующих

1) тесноту связи – индекса корреляции, парного линейного коэффициента корреляции;

2) ошибку аппроксимации;

3) качество уравнения регрессии и отдельных его параметров – средние квадратические ошибки уравнения регрессии в целом и отдельных его параметров.

Для уравнений регрессии любого вида определяется индекс корреляции, который характеризует только тесноту корреляционной зависимости, т.е. степень ее приближения к функциональной связи:

,

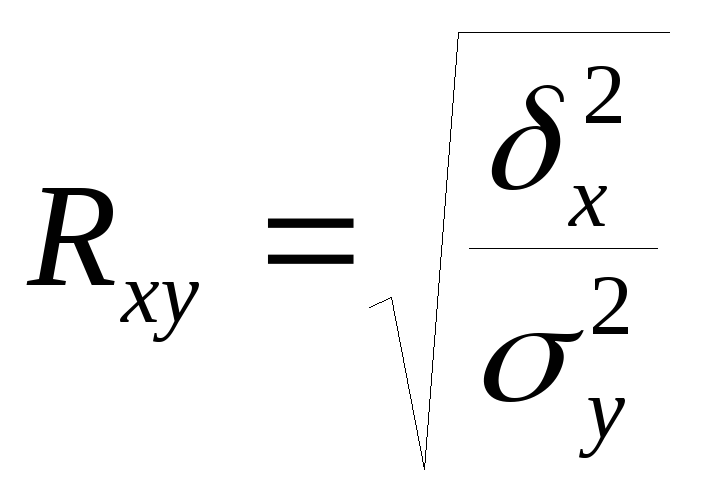где  – факторная (теоретическая) дисперсия;

 – общая дисперсия.

Индекс корреляции принимает значения , при этом,

если  – то связь между признаками отсутствует;

если  – то связь между признаками х и у является функциональной, Чем ближе к 1, тем более тесной считается связь между изучаемыми признаками. Если , то связь можно считать тесной

Дисперсии, необходимые для вычисления показателей тесноты связи вычисляются:

Общая дисперсия, измеряющая общую вариацию за счет действия всех факторов:

Факторная (теоретическая) дисперсия, измеряющая вариацию результативного признака у за счет действия факторного признака х:

Остаточная дисперсия, характеризующая вариацию признака у за счет всех факторов, кроме х (т.е. при исключенном х):

Тогда по правилу сложения дисперсий:

Качество парной линейной регрессии может быть определено также с помощью парного линейного коэффициента корреляции:

,

где  – ковариация переменных х и у;

 – среднеквадратическое отклонение независимого признака;

 – среднеквадратическое отклонение зависимого признака.

Линейный коэффициент корреляции характеризует тесноту и направление связи между изучаемыми признаками. Он измеряется в пределах [-1; +1]:

если  – то связь между признаками прямая;

если  – то связь между признаками обратная;

если  – то связь между признаками отсутствует;

если или  – то связь между признаками является функциональной, т.е. характеризуется полным соответствием между х и у. Чем ближе к 1, тем более тесной считается связь между изучаемыми признаками.

Если индекс корреляции (парный линейный коэффициент корреляции) возвести в квадрат, то получим коэффициент детерминации.

Коэффициент детерминации – представляет собой долю факторной дисперсии в общей и показывает, на сколько процентов вариация результативного признака у объясняется вариацией факторного признака х:

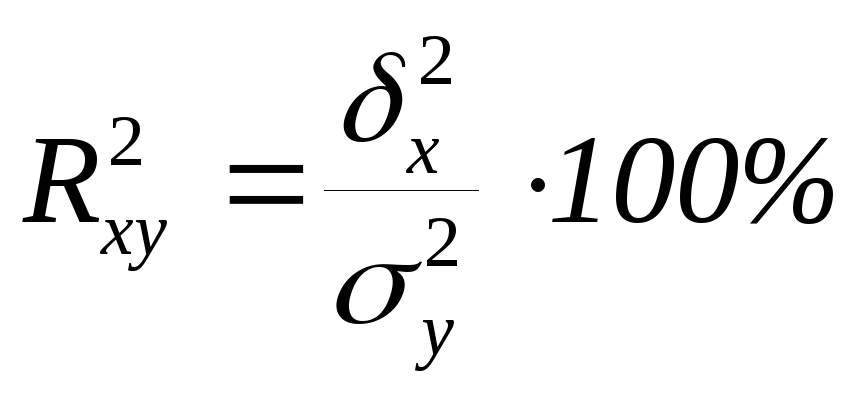
Он характеризует не всю вариацию у от факторного признака х, а лишь ту ее часть, которая соответствует линейному уравнению регрессии, т.е. показывает удельный вес вариации результативного признака, линейно связанной с вариацией факторного признака.

Величина  – доля вариации результативного признака, которую модель регрессии учесть не смогла.

Рассеяние точек корреляционного поля может быть очень велико, и вычисленное уравнение регрессии может давать большую погрешность в оценке анализируемого показателя.

Средняя ошибка аппроксимации показывает среднее отклонение расчетных значений от фактических:

Максимально допустимое значение 12–15%.

Мерой разброса зависимой переменной вокруг линии регрессии служит стандартная ошибка. Для всей совокупности наблюдаемых значений рассчитывается стандартная (среднеквадратическая) ошибка уравнения регрессии, которая представляет собой среднее квадратическое отклонение фактических значений у относительно теоретических значений, рассчитанных по уравнению регрессии у_х.

,

где  – число степеней свободы;

m – число параметров уравнения регрессии (для уравнения прямой m=2).

Оценить величину средней квадратической ошибки можно сопоставив ее

а)  со средним значение результативного признака у;

б) со средним квадратическим отклонением признака у:

если , то использование данного уравнения регрессии является целесообразным.

Отдельно оцениваются стандартные (среднеквадратические) ошибки параметров уравнения и индекса корреляции:

; ; .

_х – среднее квадратическое отклонение х.