Глава 21

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ

СЕЧЕНИЙ 21.1. Статический момент площади

При некоторых деформациях прочность деталей зависит не только от площади поперечного сечения, но и от его формы. До сих пор мы изучали деформации, у которых напряжения зависели только от площади поперечного сечения. В дальнейшем для изуче­ния деформаций кручения и изгиба нам потребуется знание неко­торых других геометрических характеристик плоских фигур.

Статическим моментом площади плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на расстояния от них до этой оси (рис. 21.1).

Статический момент площади обозна­чим S с индексом соответствующей оси:

у

S_x = J ydA\ S_y = J xdA.

А А

В теоретической механике были вы­ведены формулы для определения коор­динат центра тяжести площади фигуры:

*^{с =} Ъа, ^]Ус= Ъл> '

Так как в этих формулах под A_i можно понимать площадь dA элементарной площадки, то в пределе при dA, стремящемся к нулю, выражения, стоящие в числителях правых частей формул, будут представлять собой статические моменты площади фигуры отно­сительно осей у и х, а ^ Л_i есть площадь А всей фигуры. Следова­тельно,

S_y = | xdA = х_сА; S_x = jydA = y_cA

А А

Статический момент площади фигуры относительно оси, лежа­щей в этой же плоскости, равен произведению площади фигуры на расстояние от ее центра тяжести до этой оси.

Единица статического момента площади

[S] = [x_c][A] = m>m² =м³.

Статический момент площади фигуры может быть величиной положительной, отрицательной и равной нулю.

Очевидно, что статический момент площади относительно оси, проходящей через центр тяжести площади фигуры (центральной оси), в том числе относительно оси симметрии фигуры, равен нулю.

В теоретической механике установлено также, что в формулах для определения координат центра тяжести площади под А_{ мож­но понимать площади конечных частей фигуры, а под х_{ и у_i — ко­ординаты центров тяжести этих частей (т.е. применять метод раз­биения). Отсюда следует, что при определении статического мо­мента площади сложной фигуры также можно применять метод разбиения, т.е. определять статический момент всей фигуры как алгебраическую сумму статических моментов отдельных ее частей:

s = 5>i.

где Si — статический момент площади каждой части фигуры.

Понятие о статическом моменте площади понадобится нам в дальнейшем для определения положения центров тяжести сечений и при определении касательных напряжений при изгибе.

2. Полярный момент инерции

Полярным моментом инерции плоской фигуры отно­сительно полюса, лежащего в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на квадраты их расстояний до полюса (см. рис. 21.1).

Полярный момент инерции обозначим

Ip=\ p²dA

А

Единица полярного момента инерции

[^} ⁼ [Р²]ИЗ = м²-м² =м⁴-

Полярный момент инерции — величина всегда положительная и неравная нулю.

Так как понятие полярного момента инерции понадобится нам при изучении деформаций кручения круглых валов, то выведем формулы для определения полярных моментов инерции круглого сплошного и кольцевого сечений, принимая за полюс центры этих фигур.

1. Круг диаметром d (рис. 21.2).

Выделим бесконечно малую площадку cL4 в виде кольца шири­ной dp, находящегося на расстоянии р от полюса (р — переменная величина). Тогда dА = 2rcpdp. Определим полярный момент инер­ции:

d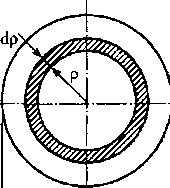

1_р - j p²cL4 = | р² -27tpdp =

АО

О

2. Кольцо размером Dxd:

D/2

F d/2

= 2тс jp³dp-~(D⁴ -d^Ay,

1_р = (гс/32)(Я⁴-</⁴) = 0Д(Д⁴-<*⁴).

Полярный момент инерции кольцевого сечения можно вычис­лить как разность полярных моментов инерции большого и малого кругов.

2. Осевой момент инерции

Осевым моментом инерции плоской фигуры относи­тельно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на квадрат расстояний от них до этой оси (см, рис. 21.1).

Осевой момент инерции обозначим I с индексом, соответствую­щим оси:

I_x = jV(L4; I_y = J x²dA

А А

Очевидно, что осевой и полярный моменты инерции выражают­ся в одинаковых единицах:

[/] = м⁴

Осевой момент инерции — величина всегда положительная и не равная нулю.

Сложим моменты инерции относительно двух взаимно-перпен­дикулярных осей хиу (см. рис. 21.1):

I_x +/_у = Jy²dA + j x²dA = j(y²+x²)dA = J p²cL4 = /_p;

AAA A*

У
4 >				•о
	?ШШа	шш
>				X
		> в		X

Рис. 21.3

Сумма осевых моментов инерции от­носительно двух взаимно-перпендику- лярных осей равна полярному моменту инерции относительно начала коорди­нат.

Так как интеграл суммы равен сумме интегралов, то момент инерции сложной фигуры можно вычислять как сумму мо­ментов инерции простых фигур, на кото­рые разбивают сложную фигуру. Поня­тие об осевых моментах инерции пона­добится нам в дальнейшем при изуче­нии теории изгиба.

Вычислим осевые моменты инерции некоторых простых фигур.

1. Прямоугольник размером bxh (рис. 21.3).

Бесконечно малую площадку dA выделим в виде полоски шири­ной Ь и высотой dу, тогда dA - bdy:

+ h/2+А/2

I_x=jy²dA = jy²bdy = j y²dy =bh³/\2)

A-A/2-h/2

I_x=bh³/12.

Для квадрата со стороной а 1_Х = а ⁴ /12.

2. Круг диаметром относительно осей л: и у. В силу симметрии для круга 1_Х - 1_у. Так как

I_x+I₉=I=nd^A/ 32,

ТО

1_х = 1_У = /_р /2 = лаГ⁴ /64 « 0,05г/⁴.

3. Кольцо размером D х d относительно осей хку: (TC/64)(D⁴ -<*⁴) -0,05(0⁴ -Л⁴).

2. Момент инерции при параллельном переносе осей

Оси, проходящие через центр тяжести фигуры, называются центральными. Момент инерции относительно центральной оси называется центральным моментом инерции.

Теорема. Момент инерции относительно какой-либо оси равен сумме момента инерции относительно центральной оси, параллель­ной данной, и произведения площади фигуры на квадрат расстояния между осями.

Пусть дана произвольная плоская фигура, площадь которой А, центр тяжести расположен в точке С, а центральный момент инерции от­носительно оси х будет 1_Х. Вычислим момент инерции фигуры относи­тельно оси x_t, параллельной цен­тральной и отстоящей от нее на рас­стоянии а (рис. 21.4):

I_Xl =\ytdA + \(y+a)²dA =

А А

= | #²cL4+2<zj ydA +a²jdA.

Первое слагаемое правой части есть момент инерции фигуры относительно оси х, т.е. 1_Х\ второе слагаемое содержит статический момент площади относительно оси х, а он равен нулю, так как ось х ~ центральная; третье слагаемое после интегрирования будет равно а² А. В результате получим

1_Г =1_г+а²Л;

•Tj X ⁷

теорема доказана.

Нужно помнить то обстоятельство, что последней формулой можно пользоваться только в тех случаях, когда одна непараллель­ных осей — центральная.

Анализируя полученную формулу, можно сделать вывод, что из ряда параллельных осей момент инерции будет наименьшим отно­сительно центральной оси.

Пользуясь доказанной теоремой, выведем формулу для вычис­ления момента инерции прямоугольника относительно оси х_р про­ходящей через основание (см. рис. 21.3):

I_XJ = I_x+a²A~bh²/\ 2 +

+ h²bh/A^bh² /Ъ.

2. Главные оси и главные моменты инерции

Представим себе плоскую фигуру, моменты инерции которой относительно осей координат равны 1_Х и 1_у, а полярный момент инерции относительно начала координат равен 1_р . Как было уста­новлено ранее,

1_Х ~/_р.

Если оси координат поворачивать в своей плоскости вокруг на­чала координат, то полярный момент инерции останется неизмен­ным, а осевые моменты инерции будут изменяться, причем

1_Х +1 _у - const.

Если сумма двух переменных величин остается постоянной, то одна из них уменьшается, а другая увеличивается. Следовательно, при каком-то положении осей один из осевых моментов достигает максимального, а другой — минимального значения.

Оси, относительно которых моменты инерции имеют макси­мальное и минимальное значения, называются главными ося­ми инерции.

Момент инерции относительной главной оси называется главным моментом инерции.

Если главная ось проходит через центр тяжести фигуры, то она называется главной центральной осью, а момент инерции относи­тельно этой оси — главным центральным моментом инерции.

Особо важным является то обстоятельство, что если фигура имеет ось симметрии, то эта ось всегда будет одной из главных центральных осей.

Введем еще одну геометрическую характеристику плоского се­чения.

Центробежным моментом инерции плоской фигу­ры называется взятая по всей площади фигуры сумма произведе­ний элементарных площадок на произведение расстояний этих площадок до двух данных взаимно-перпендикулярных осей:

А

где х,у~ расстояния от площадки сЫ до осей у их.

Центробежный момент инерции может быть положительным, отрицательным и в частном случае равным нулю.

Если взаимно-перпендикулярные оси х и у или одна из них яв­ляются осью симметрии плоской фигуры, то относительно таких осей центробежный момент инерции равен нулю.

Центробежный момент инерции входит в формулы для опреде­ления положения главных осей несимметричных сечений.

В таблицах стандартных профилей прокатных сталей содержит­ся геометрическая характеристика, которая называется радиу­сом инерции сечения и вычисляется по формулам:

Кх 4UA, ijlу /А,

где 1# 1_у — осевые моменты инерции сечения относительно цен­тральных осей; А — площадь сечения.

Эта геометрическая характеристика используется при изучении внецентренного растяжения или сжатия, а также продольного из­гиба.

Пример 21.1. Определить главные центральные моменты инерции тав­рового сечения, изображенного на рис. 21.5. Дано: Ь_] = 15 мм, h_x = 120 мм, b₂ = 120 мм, h₂ = 30 мм.

Решение. Геометрические характеристики сечений стандартных профилей прокатных сталей в таблицах ГОСТов (см., например, [7]) вы­ражаются в сантиметрах, поэтому вычисления в этом примере также про­ведем в сантиметрах.

Прежде всего определим положение центра тяжести С данного сечения, разде­ленного на два прямоугольника У и 2. Запи­шем статические моменты площади этих прямоугольников относительно оси х₃ и определим координату у_с центра тяжести С всего сечения (х_с = 0, так как сечение сим­метрично относительно оси у).

Обозначим площади прямоугольников А_х,А₂, тогда

Ус =

А_х + А2

1,5-12-0,5-12 + 12-3(12 + 0,5-3) ^

—-—— = 11 см.

1,5-12 + 12-3

Поскольку заданное сечение симметрично относительно оси у, то эта ось является одной из главных центральных осей. Определим момент инерции 1_у всего сечения как сумму моментов инерции прямоугольников

1. и 2 ,тогда

h_xb\ b₂h\ 12-1,5³ 3-12³

1— I+ /„ =

У УI У г у2

_ + = 435 см⁴. 12 12 12

Определим моменты инерции 1_Х и прямоугольников^ и 2 относи­тельно собственных центральных осей х_х и х₂:

/, ₌Ml = Wfl ₌ 216c„‘_;

12 12

_r b_xh\ 12-З³ ₄ 4, ~ —г^- = = 27 см .

12 12

Применим теорему о моментах инерции относительно параллельных осей и определим главный центральный момент инерции 1_Х относительно центральной оси х, причем

а\ = у_с - 0,5А, =11 — 0,5 *12 = 5 см;

а, - h\+0_t5h₂-y_c = 12 + 0,5 - 3 -11 = 2,5 см;

4 = 4, +«Mi+4₂ +<^Л ⁼ 216 +5² -1,5-12+ 27+ 2,5² -12-3 = 918 см⁴.

Итак, главные центральные моменты инерции заданного сечения:

4 =918 см⁴; 1_у - 435 см .