Игровые модели Основные понятия

Были рассмотрены модели, построенные на основе статистических законов. Результатом исследования этих моделей было определение вероятности наступления того или иного события и, как следствие, выполнения расчета характеристик системы массового обслуживания.

В игровых моделях статистические данные либо вообще отсутствуют, либо носят весьма приблизительный характер. В очень редких (исключительных) случаях для игровых моделей можно определить количественную оценку или указать оптимальное решение. Поэтому построение игровых моделей носит, как правило, эвристический характер с большой долей волюнтаризма. В игровых моделях не ставится задача найти какое-то числовое решение, а требуется лишь или очертить область возможных решений, или предоставить некоторые дополнительные сведения о возможном развитии событий и рекомендовать правила поведения.

Различают два больших класса игровых моделей: модели без противодействия (или их еще называют «играми с природой») и модели с противодействием (действия конкурентов на рынке).

Игры с противодействием часто называют конфликтными ситуациями, которые широко распространены в обществе. Например, конкурентная борьба в экономике, в спортивных соревнованиях, состязание сторон в ходе судебного заседания и т.д. При конфликтных ситуациях решения принимаются в условиях неопределенности двумя или более разумными противниками, каждый из которых стремится оптимизировать свои решения за счет других. Теория, занимающаяся принятием решений в условиях конфликтных ситуаций , называется теорией игр. Математическая модель конфликтной ситуации представляет собой игру.

Игра-это совокупность правил, описывающих сущность конфликтной ситуации. Эти правила устанавливают:

• Выбор образа действия игроков на каждом этапе игры;

• Информацию, которой обладает каждый игрок при осуществлении выбора;

• Плату каждого игрока после завершения любого этапа игры.

Игру можно определить следующим образом:

• Имеются n конфликтующих сторон (игроков),принимающих решения, интересы которых не совпадают

• сформулированы правила выбора допустимых стратегий, известные игрокам;

• определен набор возможных конечных состояний игры( например, выигрыш, проигрыш, ничья);

• всем игрокам заранее известны платежи, соответствующие каждому возможному конечному состоянию. Платежи задаются в виде матрицы A=(a_ij), она называется платежной матрицей или матрицей игры.

Участниками игры (конфликтной ситуации) могут быть минимум два человека (парная игра) или несколько человек (множественная игра). Каждый игрок имеет некоторое множество(конечное или бесконечное) возможных выборов т.е. стратегий. Стратегией игры называется совокупность правил, определяющих поведение игрока от начала игры до ее завершения. Если игра содержит ограниченное количество стратегий, то такая игра называется конечной. В противном случае — бесконечной.

Если игрок при выборе очередного хода придерживается каких-либо правил, то такая игра носит название стратегической. Однако игрок во время игры может менять вариант своего поведения (но не правил), т. е. сменить стратегию. Стратегия, приносящая игроку максимальный выигрыш, называется оптимальной.

Игра называется игрой с нулевой суммой, когда выигрыш одного игрока равен проигрышу другого игрока, т. е. общая сумма выигрыша всех игроков равна нулю, в противном случае она называется игрой с ненулевой суммой. Если первый игрок имеет m стратегий , а второй –n стратегий, то мы имеем дело с игрой mxn. Пусть заданы множество стратегий: для первого игрока Ai, для второго игрока-Bj, платежная матрица A=aij, где aij- выигрыш первого игрока или проигрыш второго игрока при выборе стратегий Ai и Bj соответственно. Каждый игрок выбирает некоторую стратегию, т.е. пользуется при выборе чистой стратегией. При этом решение игры будет в чистых стратегиях. При построении игровых моделей предполагается, что каждый из игроков будет выбирать только лучшую (для себя) стратегию, первый игрок стремится максимизировать свой выигрыш, а второй игрок, наоборот, минимизировать свой проигрыш. Решение игры состоит в определении наилучшей стратегии каждым игроком. Выбор наилучшей стратегии одним игроком проводится при полном отсутствии информации о принимаемом решении вторым игроком. Результатом исследования игровой модели является определение наиболее осторожной стратегии поведения игрока: либо обеспечение гарантированного выигрыша (как правило, минимального), либо сведение к минимуму проигрыша. Поэтому для решения игры двух лиц с нулевой суммой используется пессимистичный критерий. Так , если первый игрок применяет стратегию Ai, то второй будет стремится к тому, чтобы выбором соответствующей стратегии Bj свести выигрыш первого игрока к минимуму. Величина этого минимума

α_i=min a_{ij i=1,m} J

Первый игрок (при любых ответах противника) будет стремится найти такую стратегию, при которой αi обращается в максимум:

α= max α_i =max min a_ij i i J

Величина α называется нижней ценой игры. Ей соответствует максиминная стратегия, придерживаясь которой первый игрок при любых стратегиях противника обеспечит себе выигрыш, не меньший α .Нижняя цена игры является гарантированным выигрышем первого игрока при любых стратегиях второго игрока.

Аналогично определим по каждому столбцу матрицы

βj=max a_ij j=1,n J

найдем минимальное значение βj: β=min βj=min max a_ij J J i

Величина β называется верхней ценой игры. Ей соответствует минимаксная стратегия второго игрока. Величина β представляет собой гарантированный проигрыш второго игрока при любой стратегии первого игрока. Таким образом, результат исследования игровых моделей указывает на оптимальную стратегию поведения (гарантированный выигрыш), а какой стратегией воспользуется игрок в реальной жизни — дело самого игрока.

Пример.

Дана платежная матрица, которая определяет выигрыши игрока А. вычислит нижнюю и верхнюю цену заданной игры.

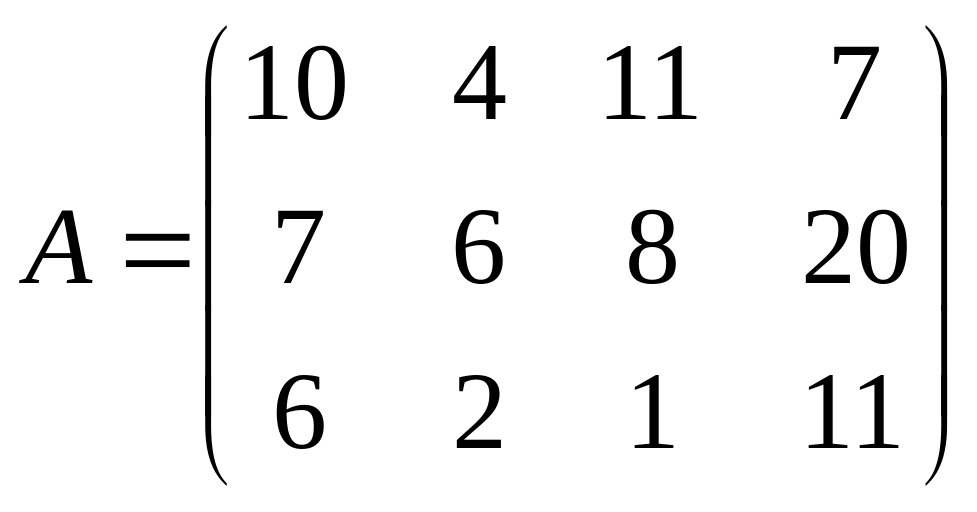
Решение

Стратегии первого игрока Аi	Стратегии второго игрока Вj				значение αi	α
	В1	В2	В3	В4
А1	10	4	11	7	4
А2	7	6	8	20	6	6
А3	6	2	1	11	1
Значение βj	10	6	11	20
β		6

При первой стратегии выигрыш игрока А будет не меньше 4 независимо от поведения игрока В и т.д. таким образом, минимальные значения α_i определяют минимально гарантированный выигрыш для игрока А, если он выбирает соответствующую стратегию i. Величина α=max α_i =6 ,будет гарантированным выигрышем игрока А при любых стратегиях игрока В. Вторая стратегия называется максиминной стратегией, а соответствующее значение выигрыша будет нижней ценой игры(минимальный гарантированный выигрыш).

Второй игрок стремится минимизировать свой проигрыш. Выбрав первую стратегию, игрок В может проиграть не более чем β1=max(10,7,6)=10независимо от выбора стратегии игроком А. и т.д. Игрок В выбирает стратегию β2,которая минимизирует его максимальные проигрыши: β=min βj=6. Эта величина будет гарантированным проигрышем игрока В при любых стратегиях игрока А. Выбранная игроком в вторая стратегия называется минимаксной стратегией, а соответствующее значение проигрыша β2=6 называется верхней ценой игры.

Следует отметить, что для любой матрицы А=( a_ij) выполняется неравенство

β>=α.

Если β= α, т.е. верхняя цена игры = нижней цене, то соответствующие чистые стратегии называются оптимальными, а игра имеет седловую точку. Седловая точка является минимальным элементом соответствующей строки и максимальным элементом соответствующего столбца. Это точка есть точка равновесия игры, определяющая однозначно оптимальные стратегии. Оптимальность здесь означает, что ни один игрок не стремится изменить свою стратегию, т.к. его противник может на это ответить выбором другой стратегии, дающий худший для первого игрока результат. Величина

с= β= α называется ценой игры. Она определяет средний выигрыш игрока А и средний проигрыш игрока В при использовании ими оптимальных стратегий.

Если в платежной матрице все элементы строки А_i не меньше соответствующих элементов строки А_k , а по крайней мере один строго больше, то строка А_i называется доминирующей, а строка А_k доминируемой. Аналогичны понятия доминирующий столбец, доминируемый столбец.

Первому игроку невыгодно применять стратегии, которым соответствуют доминируемые строки; второму игроку невыгодно применять стратегии, которым соответствуют доминирующие столбцы. Поэтому при решении игры можно уменьшить размеры платежной матрицы путем удаления из нее доминирующих столбцов и доминируемых строк.

Пример.

Для игры с платежной матрицей найдите стратегии игроков и цену игры.

Элемент а₃₂=-1 является наименьшим в третьей строке и наибольшим во втором столбце, т.е. является седловой точкой. Поэтому цена игры =-1, а оптимальные стратегии игроков: для первого А3, а второго В2.

И спользуя понятия доминируемых строк и доминирующих столбцов, задачу можно решить так. В матрице А третья строка доминирует над второй, поэтому вторую строку можно убрать из платежной матрицы. Получится матрица

В матрице А1 первый и третий столбцы доминируют над вторым, их можно убрать. Получится матрица

В матрице А2 вторая строка доминирует, ее убираем , получаем А3=(-1) Элемент матрицы А3 и определяет решение игры.