Глава. Функции нескольких переменных

§1. Функция двух переменных.

Определение 1. Переменная  называется функцией двух переменных  и , если:

1) задано множество  пар численных значений  и ; 2) задан закон, по которому каждой паре чисел  из этого множества соответствует единственное численное значение.

Обозначения: , , ,  

При этом переменные  и  называются аргументами или независимыми переменными. Определение 2. Множество  всех пар значений аргументов данной функции двух переменных называется областью определения этой функции.

Для наглядности можно считать, что наблюдается некоторый процесс, в котором некоторая точка М перемещается по плоскости. Координаты этой точки х, у являются переменными величинами, и используется запись: М(х, у). Если х, у являются переменными функции , пишут Графиком такой функции называется множество точек , удовлетворяющих равенству: . Такие точки образуют некоторую поверхность в пространстве. Поэтому графиком функции двух переменных в прямоугольной декартовой системе координат в пространстве является поверхность.

Линией уровня функции  называется множество точек М(х, у), в которых эта функция принимает постоянное значение. Такое множество является некоторой линией на плоскости, и ее уравнение имеет вид: , где С – некоторое число.

Если в рассматриваемом процессе расстояние между перемещающейся точкой М(х, у) и неподвижной точкой М₀(х₀, у₀) стремится к нулю, то говорят, что М стремится к М₀, и пишут: и . Расстояние между этими точками есть функция

Определение 3. Постоянное число b называется пределом функции при , если разность стремится к нулю при . (Говорят также, что есть величина бесконечно малая величина при ).

Обозначения: 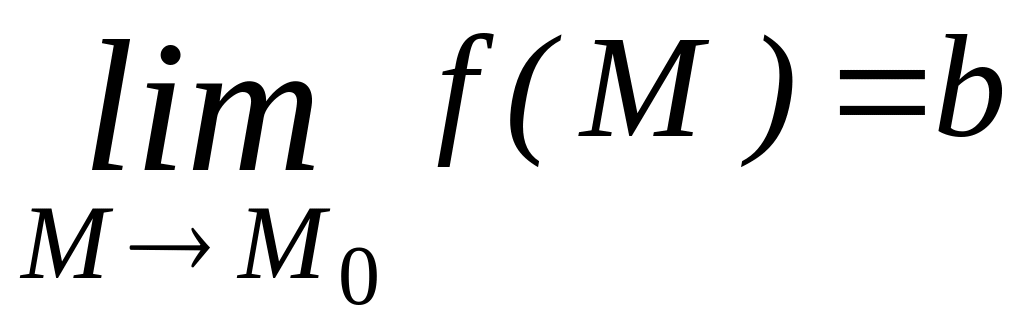или .

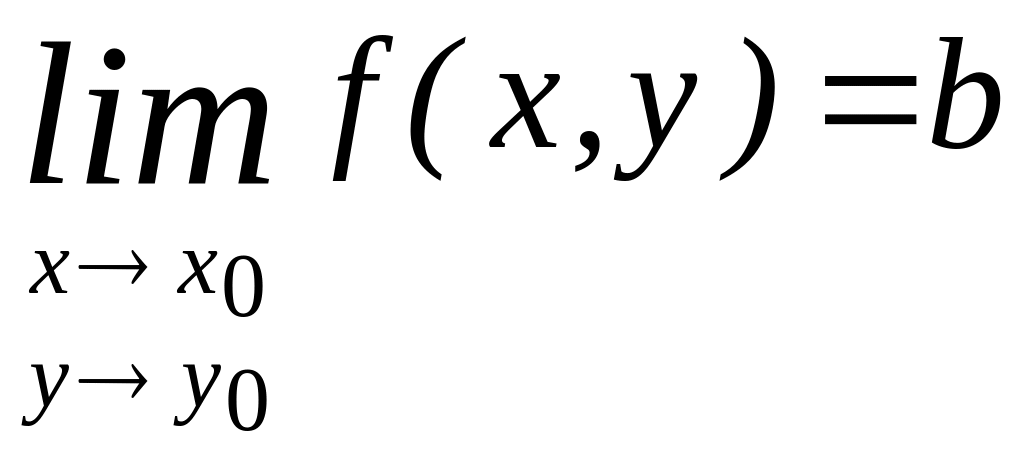Определение 4. Функция называется непрерывной в точке М₀, если она определена в некоторой окрестности этой точки и верно равенство: 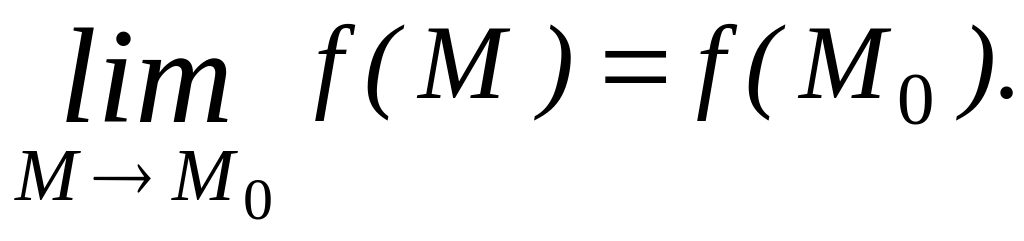Функция называется непрерывной на множестве S , если она непрерывна во всех точках этого множества.

Аналогично определяется функция трех переменных и соответствующие понятия.

§2. Производные и дифференциалы функции нескольких переменных

Рассматривается функция двух переменных _.

Определение 5. Величина называется частным приращение аргумента в точке . Величина называется частным приращением по функции в точке . Величина называется частным приращение аргумента в точке . Величина называется частным приращением по функции в точке . Определение 6. Частной производной от функции  по переменной  в точке называется предел отношения к , когда стремится к нулю, если этот предел существует: 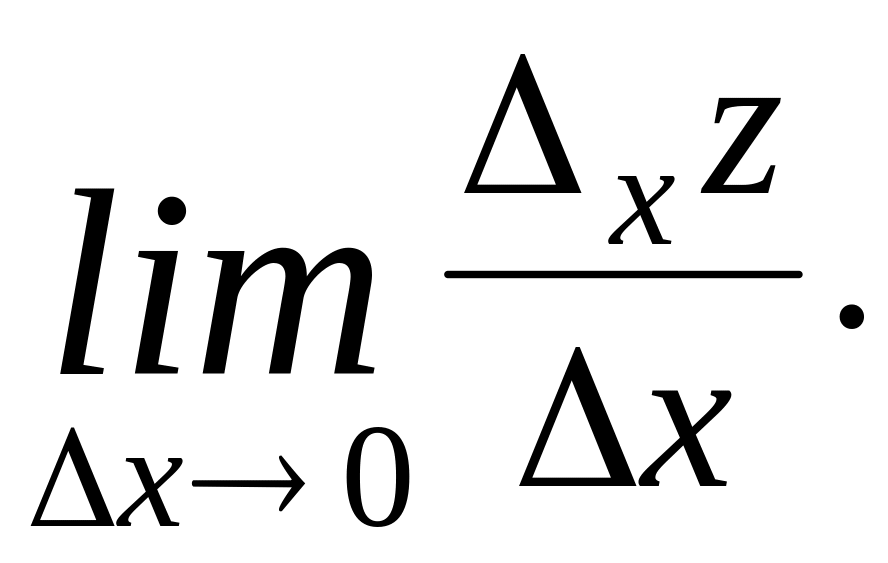Обозначение: , , , .

Частной производной от функции  по переменной  в точке называется предел отношения к , когда стремится к нулю, если этот предел существует: 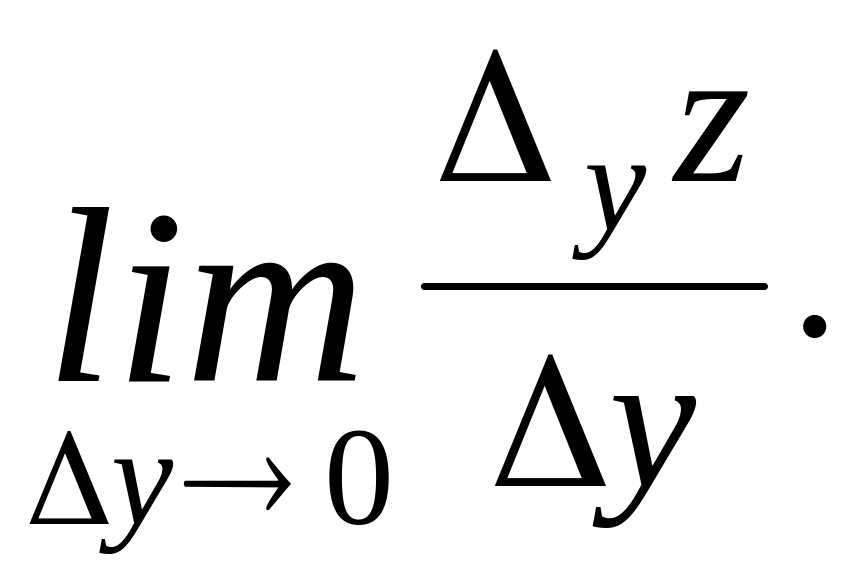Обозначение: , , , .

Определение 7. Полным приращением функции  в точке  называется разность , где  и  - приращения аргументов. Функция  называется дифференцируемой в точке , если в этой точке полное приращение можно представить в виде , где - числа и обозначает бесконечно малую величину, когда величина стремится к 0. При этом величина называется линейной частью полного приращения относительно . Определение 8. Полным дифференциалом функции  в точке называется линейная часть полного приращения относительно приращений  и . Обозначение: , Доказывается, что если функция имеет непрерывные частные производные, то ее полный дифференциал вычисляется по формуле: , где частные производные вычисляются в заданной точке. В частности, дифференциалы переменных совпадают со своими приращениями: . Поэтому Для функции трех переменных полный дифференциал вычисляется по формуле: . При достаточно малом  для дифференцируемой функции  справедливы приближенное равенство . Из этого равенства получается следующая формула, используемая для приближенного вычисления значения функции: . Определение 9. Частными производными второго порядка от функции  называются частные производные от ее частных производных первого порядка. При этом различают: частную производную по х: ; частную производную по у: ; и смешанные производные: , . Доказывается, что если смешанные производные непрерывны в рассматриваемой точке, то они равны между собой: _.

Определение 10. Дифференциалом второго порядка от функции  называется дифференциал от ее полного дифференциала, то есть . Если  и  – независимые переменные и функция  имеет непрерывные производные второго порядка, то дифференциал второго порядка вычисляется по формуле .

§3. Экстремум функции двух переменных. Функция  имеет максимум (минимум) в точке , если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке  некоторой окрестности точки , то есть  (соответственно ) для всех точек , принадлежащих этой окрестности. Максимум и минимум функции называется ее экстремумом. Точка , в которой функция имеет экстремум, называется точкой экстремума. Необходимое условие экстремума: если дифференцируемая функция  достигает экстремума в точке , то ее частные производные первого порядка в этой точке равны нулю, то есть: , . Точки, в которых частные производные равны нулю, называются стационарными точками. Стационарные точки и точки, в которых производные не существуют и которые лежат внутри области определения функции, называются критическими точками. Не всякая критическая точка является точкой экстремума. Достаточное условие существования экстремума: Пусть  стационарная точка функции . Обозначим , ,  и составим дискриминант . Тогда: если , то функция имеет в точке  экстремум, а именно максимум, при  (или ) и минимум, при  (или ); если , то в точке  экстремума нет; если , то требуется дальнейшее исследование (сомнительный случай). Пример 6. Найти экстремум функции . Решение. Находим частные производные первого порядка  и  и критические точки, в которых они равны нулю или не существуют: ; . Решая систему , найдем две точки:  и М₂(1; 0,5). Обе точки являются критическими, т.к. функция  определена на своей плоскости . Исследуем критические точки  и по знаку определителя , составленного из частных производных второго порядка: ; ; . Для точки  получим , , . . Следовательно, согласно достаточному условию в точке  нет экстремума. Для точки М₂(1; 0,5) получим , , , . Согласно достаточному условию  есть точка минимума z _min =4. Функция , непрерывная в некоторой ограниченной замкнутой области , обязательно имеет в этой области наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащих внутри области , или в точках, лежащих на границе области. Чтобы найти наибольшее (наименьшее) значение функции  в ограниченной замкнутой области , где она непрерывна, можно руководствоваться следующим: 1.     Найти критические точки, лежащие внутри области , и вычислить значения функции в этих точках (не вдаваясь в исследование, будет ли в них экстремум функции и какого вида). 2.     Найти наибольшее (наименьшее) значение функции на границе области . 3.     Сравнить полученные значения функции: самое большое (меньшее) из них будет наибольшим (наименьшим) значением функции во всей области . Пример 7. Найти наибольшее и наименьшее значения функции  в круге .

Решение. 1. = , = . 2. Найдем наибольшее и наименьшее значения функции на границе, то есть на окружности   , то для точек окружности функцию  можно представить как функцию одной переменной : , то есть , причем . Найдем наибольшее и наименьшее значения этой функции. Находим критические точки функции в интервале и вычислим значения функции в этих точках и на концах интервалов: , . Отсюда имеем критическую точку . В этой точке z = 0 . Еще осталось найти значения z в концах интервала : . 3.Выпишем полученные значения функции: 0, -4, 4. Отсюда видим, что функция имеет наибольшее значение, равное 4, и наименьшее значение, равное –4.