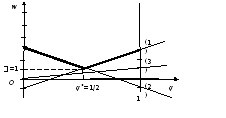Тема 2.1. Игры размера 2 × 2 и их аналитическое решение

Смотри пример 3 в разделе методических указаний по самостоятельной работе студентов.

Тема 2.2. Игры размера 2 × n и m × 2 и их графоаналитическое решение

Пример 9. Игра задана матрицей 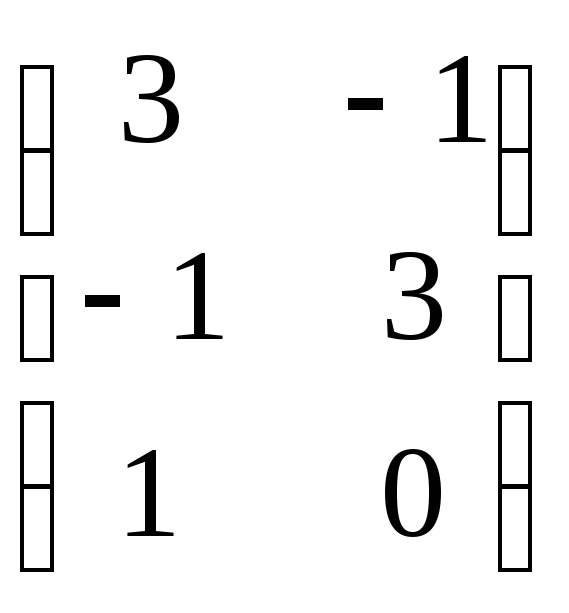. Найти решение игры графическим методом.

Нижняя цена игры равна 0, верхняя равна 3. Седловой точки нет. Решение игры нужно искать в смешанных стратегиях. Т.к. у игрока B имеются две стратегии, то рассмотрим вначале игру с точки зрения этого игрока. Ожидаемые выигрыши игрока В, соответствующие чистым стратегиям игрока A, приведены в следующей таблице (игрок B выбирает стратегию B₁ с вероятностью q, стратегию B₂ с вероятностью 1-q).

Аi wВ 1 2 3 3q+(-1)(1-q)=-1+4q -1q+3(1-q)=3-4q 1q+0(1-q)=q

Построим на координатной плоскости (q,w) все три прямые, а затем и их верхнюю огибающую (см. рис.). Нижняя точка верхней огибающей является точкой пересечения прямых (1) и (2). Решая уравнение -1+4q=3-4q, получаем q*=,=1

(игрок B смешивает свои стратегии с вероятностями, равными ; при этом цена игры равна 1).

Оптимальная смешанная стратегия игрока А определяется двумя стратегиями, которые определяют нижнюю огибающую графика. Это значит, что игрок А может смешивать стратегии А₁ и А₂. В этом случае р₁=р, р₂=1-р, р₃=0. Следовательно, ожидаемые платежи игрока А, соответствующие чистым стратегиям игрока В, имеют следующий вид.

Вj wА 1 2 -1+4p 3-4p

Приравниваем средние выигрыши игрока А, соответствующие чистым стратегиям игрока В: -1+4p=3-4p, и находим р*=1/2.

Таким образом, цена игры и оптимальные смешанные стратегии игроков А и В соответственно равны:

v=1, р^*=(,, 0),q^*=(,).

Тема 2.3. Игры размера m × n

Пример 10. Найти решение игры в смешанных стратегиях:

Обозначим чистые стратегии игроков А и В через А₁, А₂, А₃ и B₁, B₂, B₃ соответственно.

Проверим игру на наличие седловой точки: =a_ij=4,

=a_ij=6, , поэтому решение игры определяем в смешанных стратегиях. Цена игры v заключена между нижней и верхней ценами, т.е. 4v6.

Составим задачу ЛП для каждого игрока.

Для игрока А: Для игрока В:

z=х₁+х₂+х₃min, w=у₁+у₂+у₃max,

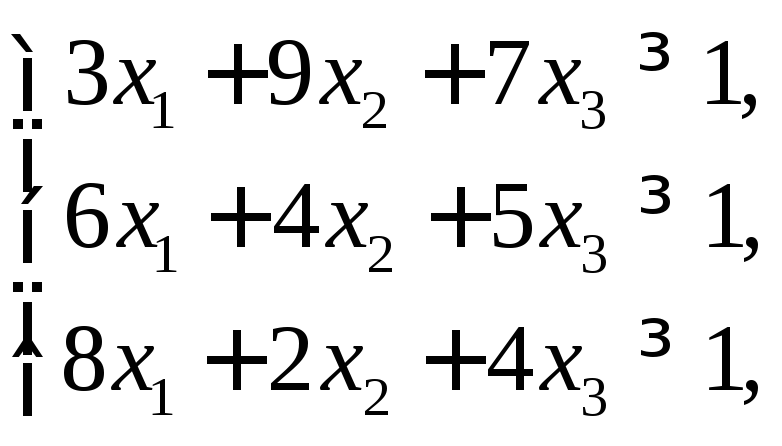
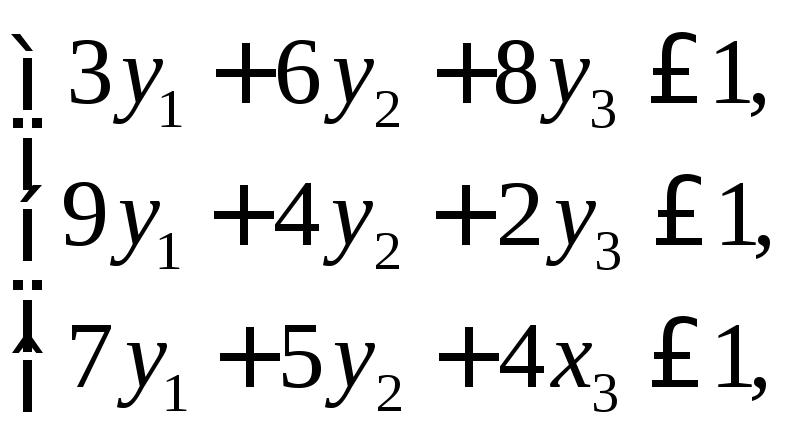
х_i0(i=1,2,3), у_j0(j=1,2,3).

(Первое неравенство для игрока A: 3p₁+9p₂+7p₃v соответствует тому, что при выборе игроком B стратегииB₁, игрок A получает выигрыш, не меньший цены игры v; далее обе части неравенства поделили на положительную величину v и ввели обозначения =x_i. Условие ν→max в переменных x теперь заменено условием z=х₁+х₂+х₃min).

Вводя балансовые переменные х₄0, х₅0, х₆0 для исходной задачи и у₄0, у₅0, у₆0 для двойственной задачи, модели задач преобразуем к канонической форме. При этом балансовые переменные двойственной задачи станут базисными.

При «ручном» счёте проще решать двойственную задачу, т.к. она не требует введения искусственных переменных. Соответствие между переменными пары взаимно двойственных задач будет следующее:

х1 х2 х3 х4 х5 х6       у4 у5 у6 у1 у2 у3

Решим, например, двойственную задачу ЛП, построенную для определения выигрыша игрока В. Каноническая форма задачи имеет вид:

w=у₁+у₂+у₃max;

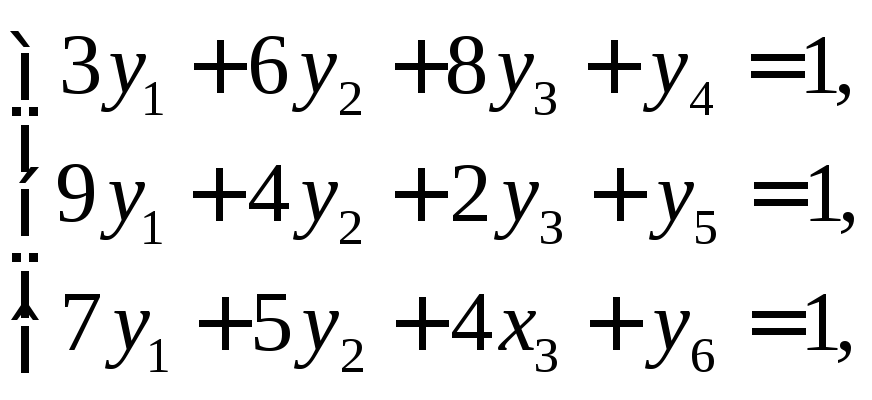
у_j0(j=1,…,6).

Решая ее симплекс-методом, имеем

БП	y1	y2	y3	y4	y5	y6	b	θ
y4	3		8	1	0	0	1	1/6
y5	9	4	2	0	1	0	1	1/4
y6	7	5	4	0	0	1	1	1/5
w	-1	-1	-1	0	0	0	0	–

БП	y1	y2	y3	y4	y5	y6	b	θ
y2	1/2	1	4/3	1/6	0	0	1/6	1/3
y5	7	0	-10/3	-2/3	1	0	1/3	1/21
y6		0	8/3	-5/6	0	1	1/6	1/27
w	-1/2	0	1/3	1/6	0	0	1/6	–

БП	y1	y2	y3	y4	y5	y6	b
y2	0	1	28/27	7/27	0	-1/9	4/27
y5	0	0	-202/27	17/27	1	-14/9	2/27
y1	1	0	16/27	-5/27	0	2/9	1/27
w	0	0	17/27	2/27	0	1/9	5/27

у*=(;…;)=(1/27; 4/27; 0; 0; 2/27; 0). При этомw*=5/27.

С учетом основной теоремы двойственности и соответствия между переменными оптимальный план исходной задачи запишется в виде

х*=(;…;)=(2/27; 0; 1/9; 0; 0; 17/27),z*=5/27.

По формулам v==,=х_i, =у_j(i=1,…,т, j=1,…,п) получим цену игры v=27/5 и вероятности идля оптимальных смешанных стратегий соответственно игроковА и В:

=27/52/27=2/5, =27/50=0, =27/51/9=3/5,

=27/51/27=1/5, =27/54/27=4/5, =27/50=0.

Таким образом, оптимальными смешанными стратегиями игроков А и В являются стратегии р*=(2/5;0; 3/5) и q*=(1/5; 4/5;0) соответственно при гарантированном получении игроком А независимо от стратегий игрока В выигрыша не менее 27/5=5,4. Проигрыш игрока В при этом составит не более 5,4.