Математика

ЭЛЕМЕНТЫ ТЕОРИИ ИГР

ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ

СОДЕРЖАНИЕ ДИСЦИПЛИНЫ

I. ВВЕДЕНИЕ

Основные понятия и определения. Классификация игр. Формальное представление игры.

II. ИГРЫ С НУЛЕВОЙ СУММОЙ

Тема 1. Выбор стратегии

Максиминная и минимаксная стратегии. Нижняя и верхняя цена игры. Решение игры в чистых стратегиях. Цена игры. Седловая точка.

Тема 2. Решение игр в смешанных стратегиях

Понятие смешанной стратегии.

Тема 2.1. Игры размера 2 × 2 и их аналитическое решение

Тема 2.2. Игры размера 2 × n и m × 2 и их графоаналитическое решение

Тема 2.3. Игры размера m × n

Приведение матричной игры к задаче линейного программирования.

III. ИГРЫ С НЕНУЛЕВОЙ СУММОЙ

Тема 3. Понятие точек равновесия

Понятие некооперативной игры. Точка равновесия по Нэшу.

IV. ИГРЫ С ПРИРОДОЙ

Тема 4. Игры с природой

Стохастические игры. Критерии Байеса и Лапласа. Нестохастические игры. Критерии Вальда, Сэвиджа, Гурвица.

СПИСОК ЛИТЕРАТУРЫ

Основная литература

1. Акулич И.Л. Математическое программирование в примерах и задачах. 2-е изд. М.: Высшая школа, 2009.-346 с.

2. Красс М.С., Чупрынов Б.П. Математика для экономистов .СПб.:Питер,. 2009. -464 с.

3. Кремер Н. Ш., Путко Б. А., Тришин И. М., Фридман М. Н. Под ред. Кремера Н.Ш. Исследование операций в экономике. М.: Юрайт, , 2-е изд., доп. и перераб., 2011.- 430 с.

4. Протасов И.Д. Теория игр и исследование операций. Учебное пособие. М.: Гелиос АРВ, 2006.

Дополнительная литература

1. Нейман.Дж.фон, Моргенштерн О. Теория игр и экономическое поведение. М.: Наука,1970. - 708 с.

2. Меньшиков И.С. Лекции по теории игр и экономическому моделированию. М.: МЗ Пресс, 2006. - 208 с.

3. Розен В.В. Математические модели принятия решений в экономике. М.: Высшая школа, 2002. - 288 с.

4. Шень А. Игры и стратегии с точки зрения математики. М.: МЦНМО, 2007. - 40 с.

5. Шикин Е.В., Шикина Г.Е. Исследование операций. М.: ТК Велби, 2006. - 280с.

Методические указания по самостоятельной работе студентов

В данном разделе в соответствии с учебной программой содержатся краткие теоретические основы и примеры решения типовых задач по основным темам курса.

Самостоятельная работа над предложенным учебным материалом поможет студентам выполнить необходимые контрольные работы и подготовиться к сдаче итогового зачета.

I. Введение

1. Основные понятия и определения

Теория игр занимается задачами построения математических моделей принятия оптимальных решений в условиях конфликта и неопределенности и методами их решения.

1. В игре участвует некоторое количество (множество) заинтересованных сторон – игроки.

2. Возможные действия каждой из сторон – ходы или стратегии.

3. Интересы сторон представлены для каждого из игроков функциями выигрыша (платежа), эти функции можно трактовать как функции полезности для каждой из сторон.

4. Предполагается, что каждый из игроков знает не только множество своих стратегий и собственную целевую функцию(функцию выигрыша), но также обладает полной и точной информацией о стратегиях и функциях выигрыша всех остальных игроков.

Таким образом, целевые функции и множества стратегий, доступные каждому из игроков, общеизвестны. В соответствии с этой информацией каждый игрок организует свое поведение и действия.

2. Классификация игр

1. В зависимости от числа заинтересованных сторон различают игры с двумя, тремя и более участникам (парные и множественные игры).

2. По количеству стратегий различают игры конечные и бесконечные.

При конечном числе стратегий их называют чистыми стратегиями (например, в игре в орлянку - две чистые стратегии: орел и решка).

В бесконечных играх игроки обладают бесконечным числом возможных стратегий (в ситуации Продавец – Покупатель каждый из игроков может назвать любую устраивающую его цену и количество продаваемого или покупаемого товара).

3. По свойствам функций выигрыша различают:

1) игры с нулевой суммой или антагонистические (выигрыш одного игрока равен проигрышу другого);

2) игры с постоянной разностью (игроки выигрывают и проигрывают одновременно и потому им выгодно действовать сообща);

3) игры с ненулевой суммой (имеются и конфликты, и согласованные действия игроков).

4. В зависимости от возможности предварительных переговоров между игроками различают кооперативные и некооперативные игры.

В кооперативных играх образуются коалиции и принимаются взаимообязывающие соглашения о стратегиях.

3. Формальное представление игры

Пусть имеются два игрока: игрок I и игрок II. Множество Х – это множество всех допустимых стратегий (действий) игрока I, а множество Y –множество всех допустимых стратегий игрока II. Пусть эти множества конечны, т.е. Х = {Х₁, Х₂,…, Х_m}, Y = {Y₁, Y₂,…,Y_n}.

В случае, если игрок I выбирает стратегию X_iХ (i=1,…,m), а игрок II – стратегию Y_jY(j=1,…,n), возникает некоторая ситуация (x_i, y_j) = _ij  Ω, где Ω есть множество возможных исходов игры.

Для сокращения записей обычно отождествляют стратегии игроков с их номерами, т.е. полагают X = {1, 2, … , m}, Y = {1, 2, … , n}, _ij= (i,j).

Для оценки исходов игры задаются целевые функции каждого игрока(функции выигрыша) (иногда используют термин «функция потерь»).

Пусть а_ijесть выигрыш игрока I в ситуации ω_ij, а b_ij – выигрыш игрока II. Таким образом, имеются две матрицы:

А = ||a_ij|| =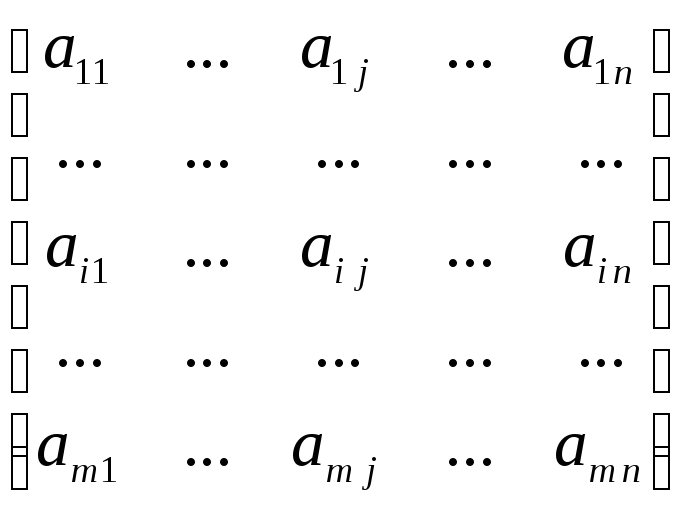иB= ||b_ij|| =.

а_ij – есть выигрыш игрока I в том случае, когда он выбирает свою i-ю стратегию, а игрок II свою j-ю стратегию;

b_ij – есть выигрыш игрока II в той же ситуации.

Если у какого-либо игрока в некоторой ситуации «выигрыш» окажется отрицательным числом, то говорят о «проигрыше». Матрицы А и В называются матрицами выигрыша, или платежными матрицами, а игра называется биматричной игрой.

В случае антагонистической игры В = –А. Это означает, что выигрыш игрока II в любой ситуации равен по величине и противоположен по знаку выигрышу игрока I в той же ситуации: b_ij = – а_ij, т.е. а_ij+ b_ij= 0 для всех i=1,…,m и j=1,…,n. В этом случае матрица В фактически не нужна, мы имеем игру с одной лишь матрицей А, или матричную игру. Далее мы будем говорить, что в ситуации _ij игрок I имеет выигрыш а_ij, а игрок II имеет проигрыш а_ij .

Игра с постоянной (необязательно нулевой) суммой (а_ij+ b_ij= с) очевидно сводится к матричной игре с матрицей А' = ||а'_ij|| = ||а_ij– c||. Иногда матричной называют именно такую игру, поскольку для ее задания достаточно одной матрицы.

Пример игры с нулевой суммой.

Игра в орлянку: каждый из игроков имеет две стратегии – «Орел» и «Решка».

Если оба выбирают одинаковые стратегии, 1-ый игрок выигрывает 10 ед., а 2-ой проигрывает 10 ед. Если они выбирают разные стратегии, то 2-ой выигрывает 10 ед., а 1-ый игрок проигрывает 10 ед.

Матрица выигрышей 1-го игрока или проигрышей 2-го

Пример игры с ненулевой суммой.

Две фирмы функционируют на рынке с одинаковым товарным объемом V. У обеих фирм по соображениям рентабельности есть следующие стратегии: либо выбросить на рынок полный объем товара V, либо выбросить половину объема 0,5V. Если 1-я фирма выбрасывает на рынок полный объем V, а 2-я – половину объема 0,5V, то 1-я получит 100% запланированной прибыли, а 2-я – только 25%, и наоборот. Если обе фирмы выбросят на рынок по полному объему V, то получат по 15% прибыли. Если по 0,5V, то прибыль каждой фирмы составит по 50% запланированной.

Биматрица выигрышей