
- •Математика
- •Методические указания по самостоятельной работе студентов
- •I. Введение
- •II. Игры с нулевой суммой
- •Тема 1. Выбор стратегии
- •Тема 2. Решение игр в смешанных стратегиях
- •Тема 2.1. Игры размера 2 × 2 и их аналитическое решение
- •Тема 2.2. Игры размера 2 × n и m × 2 и их графоаналитическое решение
- •Тема 2.3. Игры размера m × n
- •III. Игры с ненулевой суммой
- •Тема 3. Понятие точек равновесия
- •Точка равновесия по Нэшу
- •IV. Игры с природой
- •Тема 4. Игры с природой
- •Стохастическая задача Критерий Байеса (Лапласа).
- •Нестохастическая задача
- •Тема 2.1. Игры размера 2 × 2 и их аналитическое решение
- •Тема 2.2. Игры размера 2 × n и m × 2 и их графоаналитическое решение
- •Тема 2.3. Игры размера m × n
- •Тема 3. Понятие точек равновесия
- •Тема 4. Игры с природой
- •Примерные варианты контрольных работ
- •Задания для самостоятельной работы (с ответами)
Тема 2.3. Игры размера m × n
Приведение матричной игры к задаче линейного программирования
Рассмотрим
игру размерности ![]() .
.
Оптимальная
стратегия ![]() обеспечивает игроку I
средний выигрыш не меньший, чем цена
игры
обеспечивает игроку I
средний выигрыш не меньший, чем цена
игры ![]() ,
при любой стратегии игрока II
и выигрыш, равный цене игры
,
при любой стратегии игрока II
и выигрыш, равный цене игры ![]() ,
при оптимальной стратегии игрока II.
,
при оптимальной стратегии игрока II.
Математическое
ожидание выигрыша игрока
I,
если он применяет смешенную стратегию
![]() против чистой стратегии
против чистой стратегии ![]() игрока II
вычисляется
по формуле
игрока II
вычисляется
по формуле
![]()
Для
оптимальной стратегии ![]() все
математические ожидания выигрыша
(средние выигрыши) не меньше цены игры
все
математические ожидания выигрыша
(средние выигрыши) не меньше цены игры
![]() ,
поэтому получаем
,
поэтому получаем
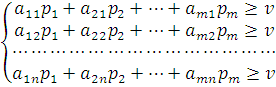
Разделим
все неравенства на ![]() и введем новые переменные:
и введем новые переменные:
![]()
![]()
Получим систему:
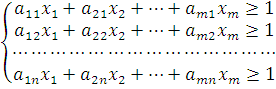
![]()
![]()
Максимизация
цены игры ![]() равносильна минимизации
равносильна минимизации ![]() .
.
Задача принимает следующий вид:
найти
значения переменных ![]() ,
удовлетворяющие
ограничениям
,
удовлетворяющие
ограничениям
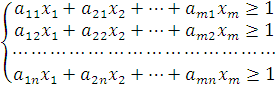
и минимизирующие функцию
![]()
Это задача линейного программирования.
Для
определения оптимальной стратегии ![]() надо учесть, что: игрок II
стремится минимизировать гарантированный
проигрыш, т.е.
надо учесть, что: игрок II
стремится минимизировать гарантированный
проигрыш, т.е. ![]() математическое
ожидание проигрыша (среднего проигрыша)
игрока II
не превосходит цены игры, какую бы чистую
стратегию ни применял игрок I:
математическое
ожидание проигрыша (среднего проигрыша)
игрока II
не превосходит цены игры, какую бы чистую
стратегию ни применял игрок I:
![]()
Тогда,
если произвести преобразования
аналогичные действиям для нахождения
![]() и обозначить
и обозначить ![]() для
для ![]() ,
задача примет вид задачи линейного
программирования.
,
задача примет вид задачи линейного
программирования.
Найти
значения переменных ![]() ,
удовлетворяющие
ограничения
,
удовлетворяющие
ограничения ![]() и максимизирующие функцию
и максимизирующие функцию ![]()
Составим
расширенные матрицы для задач нахождения
![]() и
и ![]() :
:
![]()
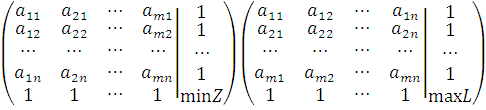
Одна
матрица получается из другой
транспонированием; в одной условия
«![]() »
в другой «
»
в другой «![]() »;
в одной задаче целевая функция на минимум
в другой на максимум. Вывод: имеем пару
симметричных двойственных задач.
»;
в одной задаче целевая функция на минимум
в другой на максимум. Вывод: имеем пару
симметричных двойственных задач.
Значит, при определении оптимальных стратегий в конкретных задачах при «ручном» счёте надо выбрать ту из двойственных задач, решение которой менее трудоемко, а решение другой найти с помощью теорем двойственности.
Пример
5.
Предприятие может выпускать три вида
продукции ![]() ,
получая при этом прибыль, зависящую от
спроса, который может быть в одном из
четырех состояний
,
получая при этом прибыль, зависящую от
спроса, который может быть в одном из
четырех состояний ![]() .
.
Дана
матрица, элементы которой ![]() характеризуют прибыль, которую получит
предприятие при выпуске
характеризуют прибыль, которую получит
предприятие при выпуске ![]() –й
продукции с
–й
продукции с ![]() –м
состоянием спроса.
–м
состоянием спроса.
|
|
|
|
|
|
|
|
3 |
3 |
6 |
8 |
|
|
9 |
10 |
4 |
2 |
|
|
7 |
7 |
5 |
4 |
Определить оптимальные пропорции выпускаемой продукции, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным.
Решение. Задача сводится к игровой модели, в которой игра предприятия (игрок I) против спроса (игрок II) задана платежной матрицей
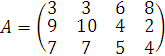 .
.
Прежде чем решать задачу, надо попытаться упростить игру.
Проводим анализ платежной матрицы и отбрасываем стратегии дублирующие или заведомо невыгодные.
Цель II игрока – уменьшить выигрыш игрока I, поэтому 2-я стратегия игрока II ему не выгодна (все элементы второго столбца не меньше элементов первого столбца).
Получим
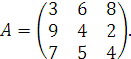
Находим
нижнюю и верхнюю цену игры:![]() ,
,
![]() .
.
Т.к.
![]() ,
седловая точка отсутствует. Решать
задачу надо в смешанных стратегиях.
,
седловая точка отсутствует. Решать
задачу надо в смешанных стратегиях.
Необходимо
найти ![]() и
и ![]() .
Вводим
обозначения
.
Вводим
обозначения ![]() ,
,
![]() и
и ![]() ,
, ![]() .
Составим
пару двойственных задач.
.
Составим
пару двойственных задач.
Задача I
![]()
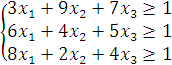
![]()
Задача II
![]()
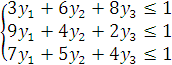
![]()
Решаем симплекс методом задачу II, т.к. после приведения к каноническому (основному) виду она будет иметь исходный опорный план.
Оптимальное базисное решение задачи II:
![]() .
.
С помощью соотношений двойственности находим оптимальное базисное решение задачи I:
![]() .
.
Найдем
цену игры ![]()
Оптимальная
стратегия игрока I![]() находится по формулам
находится по формулам ![]() .
.
![]() ;
;![]() ;
;![]()
Что
означает, предприятие должно выпускать
40% продукции ![]() и 60% продукции
и 60% продукции ![]() ,
а продукцию
,
а продукцию ![]() не выпускать.
не выпускать.
Оптимальная
стратегия спроса ![]() определяется аналогично:
определяется аналогично:
![]() .
.
![]() ( вспомнили, что второй столбец исходной
матрицы был отброшен как невыгодный).
( вспомнили, что второй столбец исходной
матрицы был отброшен как невыгодный).
Значит,
оптимальный спрос в 20% находится в
состоянии ![]() и в 80% –
в состоянии
и в 80% –
в состоянии ![]() .
.
На практике реализация оптимального решения в смешанных стратегиях может происходить несколькими путями.
Первый
состоит в физическом смешении чистых
стратегий ![]() в пропорциях, заданных вероятностями
в пропорциях, заданных вероятностями
![]() .
.
Другой путь – при многократном повторении игры – чистые стратегии применяются в виде случайно последовательности, причем каждая из них – с частотой, равной ее вероятности в оптимальном решении.

