
- •Математика
- •Методические указания по самостоятельной работе студентов
- •I. Введение
- •II. Игры с нулевой суммой
- •Тема 1. Выбор стратегии
- •Тема 2. Решение игр в смешанных стратегиях
- •Тема 2.1. Игры размера 2 × 2 и их аналитическое решение
- •Тема 2.2. Игры размера 2 × n и m × 2 и их графоаналитическое решение
- •Тема 2.3. Игры размера m × n
- •III. Игры с ненулевой суммой
- •Тема 3. Понятие точек равновесия
- •Точка равновесия по Нэшу
- •IV. Игры с природой
- •Тема 4. Игры с природой
- •Стохастическая задача Критерий Байеса (Лапласа).
- •Нестохастическая задача
- •Тема 2.1. Игры размера 2 × 2 и их аналитическое решение
- •Тема 2.2. Игры размера 2 × n и m × 2 и их графоаналитическое решение
- •Тема 2.3. Игры размера m × n
- •Тема 3. Понятие точек равновесия
- •Тема 4. Игры с природой
- •Примерные варианты контрольных работ
- •Задания для самостоятельной работы (с ответами)
III. Игры с ненулевой суммой
Тема 3. Понятие точек равновесия
Игроки могут выигрывать и проигрывать одновременно. Интересы игроков не являются полностью противоположными, и их поведение становится более разнообразным.
Ситуация характерная для рыночных отношений.
В игре с ненулевой суммой становится желательным координировать свои действия с партнером (кооперативная игра) либо каким-то образом влиять на его действия (некооперативная игра).
В случае некооперативных игр важным является определение точек равновесия игры.
Понятие равновесия в ТИ шире понятия оптимизации и включает последнее в качестве частного случая.
Точка равновесия по Нэшу
Пара
стратегий ![]() и
и
![]() для игроков I
и II
называется точкой равновесия по Нэшу,
если обоим игрокам невыгодно отклоняться
от своей стратегии в одиночку. Это
значит, что
для игроков I
и II
называется точкой равновесия по Нэшу,
если обоим игрокам невыгодно отклоняться
от своей стратегии в одиночку. Это
значит, что
![]()
Здесь
![]() – выигрыш игрока I,
– выигрыш игрока I,
![]() – выигрыш игрока II
при соответствующих стратегиях.
– выигрыш игрока II
при соответствующих стратегиях.
Пример
6.
Определить
точку равновесия для игры с биматрицей
выигрышей 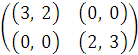 .
.
В этой игре игроку I невыгодно отклонятся от 1-й стратегии, если игрок II придерживается своей 1-й стратегии. В то же время игроку II в одиночку невыгодно отклоняться от 1-й стратегии, если ее придерживается игрок I. Аналогичная ситуация будет, если оба игрока придерживались своих 2-ых стратегий.
Значит в этой игре две точки равновесия по Нэшу: (1, 1) и (2, 2).
В ТИ доказано, что для любой конечной некооперативной игры с ненулевой суммой всегда существует, по крайней мере, одна равновесная пара смешанных стратегий; в общем случае равновесное решение может быть неединственным, причем каждому из них могут соответствовать разные значения выигрышей у игроков.
IV. Игры с природой
Тема 4. Игры с природой
Задачи, содержащие неопределенность и не имеющие конфликтного содержания (например, планирование спроса на сезонные товары).Это нестратегические игры. У противника нет стратегий, а поэтому невозможно предугадывать ходы противника исходя из предположения, что тот поступает наиболее неблагоприятным способом для нас.
У
противника есть только предполагаемые
состояния, которые можно назвать
«стратегиями природы»: ![]() .
Природа – игрок, не имеющий конкретной
цели и выбирающий очередной ход случайным
образом.
.
Природа – игрок, не имеющий конкретной
цели и выбирающий очередной ход случайным
образом.
Матрица выигрышей не является определяющей при выборе оптимального решения, она не дает полной информации. При решении «игр с природой» вводят понятие риска, который показывает, насколько удачно выбрана данная стратегия в данной ситуации.
Риском
игрока при использовании стратегии ![]() при состоянии природы
при состоянии природы ![]() называется
называется
![]()
Можно
составить матрицу рисков с элементами
![]() .
.
Стохастическая задача Критерий Байеса (Лапласа).
Вероятности
состояний «природы» ![]() известны или могут быть определены.
известны или могут быть определены.
Выбирается стратегия игрока против природы, которая максимизирует математическое ожидание его выигрыша.
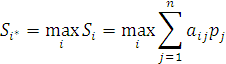
![]() -
математическое ожидание выигрыша при
использовании
-
математическое ожидание выигрыша при
использовании ![]() -й
стратегии,
-й
стратегии,
![]() - искомая оптимальная стратегия игрока,
- искомая оптимальная стратегия игрока,
![]() - элементы матрицы выигрышей,
- элементы матрицы выигрышей,
![]() - вероятности состояний «природы».
- вероятности состояний «природы».
Оптимальная в смысле максимума выигрыша стратегия дает минимальный средний риск, т.е. на ней достигается
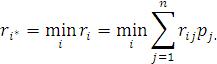
Если вероятности состояний природы в принципе существуют, но заранее неизвестны, то
полагают все состояния равновероятными (принцип недостаточного основания Лапласа);
получают искомые вероятности методом экспертных оценок;
корректируют неточные значения вероятностей с помощью специальных экспериментов.
Пример 7. При различных состояниях экономики, предприятие, обладающее определенными возможными стратегиями планирования выпуска продукции, может получить различный доход, который задан матрицей выигрышей
|
11 |
15 |
9 |
6 |
|
13 |
4 |
14 |
7 |
|
10 |
10 |
10 |
10 |
|
9 |
11 |
15 |
13 |
|
8 |
3 |
|
|
Составить
матрицу рисков предприятия. Определить
оптимальную стратегию, если 1) все
состояния экономики равновероятны
(критерий Лапласа); 2) вероятности
состояний экономики: ![]()
![]() .
.
Решение. Прежде чем решать задачу, проводим анализ платежной матрицы и отбрасываем стратегии заведомо невыгодные.
Цель I игрока – увеличить свой выигрыш, поэтому 5-я стратегия ему не выгодна (все элементы пятой строки меньше соответствующих элементов других строк).
Рассчитаем
риски по формуле ![]() .
.
Получаем матрицу рисков предприятия:
|
2 |
0 |
6 |
7 |
|
0 |
11 |
1 |
6 |
|
3 |
5 |
5 |
3 |
|
4 |
4 |
0 |
0 |
Предполагаем,
что все состояния экономики равновероятны
(критерий Лапласа). Тогда вероятности
всех состояний экономики ![]() .
Находим для каждой стратегии математическое
ожидание выигрыша и выбираем стратегию
с максимальным найденным значением.
.
Находим для каждой стратегии математическое
ожидание выигрыша и выбираем стратегию
с максимальным найденным значением.
![]()
![]()
![]()
![]()
Максимальное математическое ожидание выигрыша 12 по критерию Лапласа дает стратегия 4.
Решаем
задачу по критерию Байеса при ![]()
![]() .
Снова находим для каждой стратегии
математическое ожидание выигрыша и
выбираем стратегию с максимальным
найденным значением.
.
Снова находим для каждой стратегии
математическое ожидание выигрыша и
выбираем стратегию с максимальным
найденным значением.
![]()
![]()
![]()
![]()
Максимальное математическое ожидание выигрыша 11,7 по критерию Байеса дает стратегия 1.
