лекции Каюмова по сопромату

Рис.8.2

Некоторые компоненты материалов обладают свойствами жидкости, поэтому с течением времени образцы из таких материалов под нагрузкой

температурах, бетон, дерево, пластики – при обычных температурах). Это явление называется ползучестью материала.

Рис.8.3

Для жидкости справедлив закон: чем больше сила, тем больше скорость движения тела в жидкости. Если это соотношение линейно (т.е.

сила пропорциональна скорости), то можно записать его в виде:

Если перейти к относительным силам и относительным удлинениям,

32

они пропорционально перемещениям, получим:

Согласно закону сохранения: никакая работа не исчезает, она

тратится на совершение другой работы или переходит в другую энергию

(энергия – это работа, которую может совершить тело.).

возникающих в нашем теле. Чтобы подсчитать эту работу учтем, что тело можно считать состоящим из малых упругих частиц. Рассмотрим одну из них:

Со стороны соседних частиц на него действует напряжение . Равнодействующая напряжений будет dN

33

Вычислим работу dW, которую совершает сила dN (здесь также учитывается, что силы dN начинают возрастать постепенно и возрастают они пропорциональны перемещениям):

6) Принцип возможных перемещений.

Это один из вариантов записи закона сохранения энергии.

Пусть на брус действуют силы F1, F2,…. Они вызывают в теле

возможные перемещения вызовут в теле дополнительные возможные деформации (x, y, z) . Они приведут к появлению дополнительных внешних

сил и напряжений F1 , F2 ... , δ .

Вычислим работу внешних сил на дополнительных возможных малых перемещениях:

F

приложены силы F1, F2, …

Рассмотрим снова малый элемент с поперечным сечением dA и длиной dz (см. рис.8.5. и 8.6.). Согласно определению дополнительное удлинениеdz этого элемента вычисляется по формуле:

34

dz = dz.

Сила растяжения элемента будет:

dN = ( +δ ) dA ≈ dA.

Работа внутренних сил на дополнительных перемещениях вычисляется для малого элемента следующим образом:

dW = dN dz = dA dz = dV.

Суммируя энергию деформации всех малых элементов получим

полную энергию деформации: W dV

V Закон сохранения энергии W = U дает:

Это соотношение и называется принципом возможных перемещений (его называют также принципом виртуальных перемещений). Аналогично можно рассмотреть случай, когда действуют еще и касательные напряжения. Тогда можно получить, что к энергии деформации W добавится следующее слагаемое:

Здесь - касательное напряжение, - сдвиг малого элемента. Тогда принцип возможных перемещений примет вид:

В отличие от предыдущей формы записи закона сохранения энергии здесь нет предположения о том, что силы начинают возрастать постепенно и возрастают они пропорционально перемещениям.

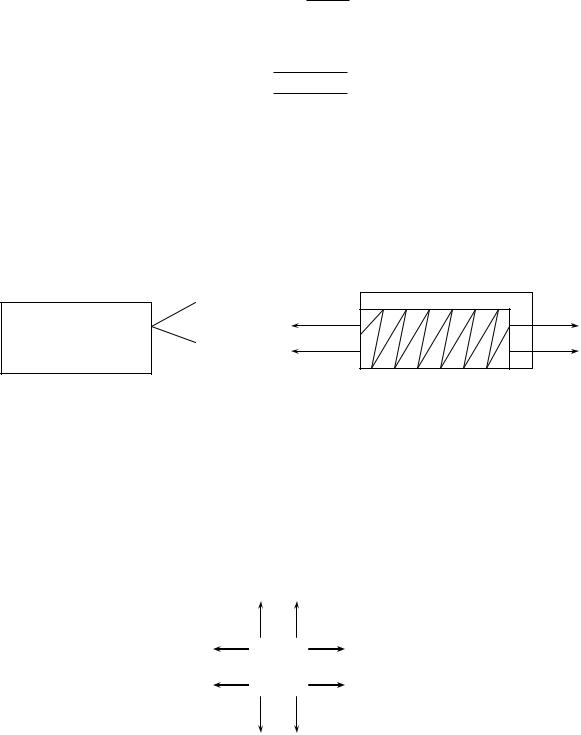
7) Эффект Пуассона.

Рассмотрим картину удлинения образца:

в 0

в

а

а 0

Рис.8.7

Явление укорочения элемента тела поперек направления удлинения называется эффектом Пуассона.

Найдем продольную относительную деформацию.

продоль а 0 .

а

35

Поперечная относительная деформация будет:

Коэффициентом Пуассона называется величина:

Для изотропных материалов (сталь, чугун, бетон) коэффициент Пуассона

0 0,5 .

Это означает, что в поперечном направлении деформация меньше продольной.

Примечание. Современные технологии могут создать композиционные материалы, у которых коэффициент Пуассона >1, то есть поперечная деформация будет больше, чем продольная. Например, это имеет место для материала, армированного

Еще более удивительным является материал, приведенный на (рис.8.9.), причем для такого армирования имеет место парадоксальный результат – продольное удлинение ведет к увеличению размеров тела и в поперечном направлении.

8) Обобщенный закон Гука.

Рассмотрим элемент, который растягивается в продольном и поперечном направлениях. Найдем деформацию, возникающую в этих направлениях.

36

Эти соотношения называются обобщенным законом Гука.

Интересно, что при записи закона Гука делается предположение о независимости деформаций удлинения от деформаций сдвига (о независимости от касательных напряжений, что одно и то же) и наоборот. Эксперименты хорошо подтверждают эти предположения. Забегая вперед, отметим, что прочность напротив сильно зависит от сочетания касательных и нормальных напряжений.

Примечание: Приведенные выше законы и предположения подтверждаются многочисленными прямыми и косвенными экспериментами, но, как и все другие законы, имеют ограниченную область применимости.

37

9. ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ ЗАКОНОВ МЕХАНИКИ ДЛЯ РАСЧЕТА СТРОИТЕЛЬНЫХ СООРУЖЕНИЙ

9.1.Расчет статически неопределимых систем

9.1.1.Статически неопределимая железобетонная колонна

Рис.9.2

На это сечение сила давления F распределяется не одинаково, хотя суммарно имеет место равенство:

Уравнение (9.1) имеет бесконечное множество решений. Уравнений равновесия для однозначного определения сил сжатия бетона и арматуры записать не удается. Поэтому задача называется статически неопределимой. Поскольку методами теоретической механики выбрать решение, отвечающее реальности, невозможно, то для этого используем свойство тел деформироваться по закону Гука, т.е. кинематические соображения. Из рисунка рис.9.1 видно, что и бетон, и арматура укорачиваются одинаково, т.е.

Это соотношение называется уравнением совместности деформации.

Подставим сюда закон Гука.

38

Тогда получим:

Вывод: хотя арматуры в колонне в два раза меньше чем бетона, но она воспринимает основную часть нагрузки (а именно - 71% нагрузки).

9.1.2 Температурные напряжения

Рассмотрим ту же колонну, но не нагруженную. Пусть в ней произошел перепад температуры на 100 . Примем следующие исходные данные (они снова приняты таковыми только для демонстрации метода отыскания температурных напряжений).

Дано:

Решение:

От перепада температур в несвязанных арматуре и бетоне деформации были бы разные. Но в колонне они воздействуют друг на друга, следовательно:

39

Поскольку неизвестных два, а уравнение одно, то снова привлечем геометрические соображения. Из рисунка видно, что и бетон, и арматура

Запишем выражения для удлинений с учетом закона Гука и ДюгамеляНеймана:

Подставим в условие совместности деформации (9.3). С учетом исходных данных получим:

Таким образом, имеем систему уравнений (9.2), (9.4):

Знак «+» говорит о том, что колонна удлинилась. Можно подсчитать напряжения:

40