лекции Каюмова по сопромату

Отсюда:

Jx

T =1 – единичная сила, приложенная в интересующем нас направлении

Еще раз напомним, что физический смысл формулы Мора заключается в том, что работа силы Т на искомом перемещении vВ равна работе внутренних сил, вызванных этой силой, на деформациях от внешних сил.

Примечания.

1.Для удобства вычислении обычно принимают, что Т=1.

2.Работой касательных напряжений обычно пренебрегают ввиду ее малости по сравнению с W.

3. При необходимости вычисления угла наклона балки α вместо единичной фиктивной силы Т необходимо прикладывать единичный момент m=1 в интересующей нас точке. Формула Мора примет вид

16.1.1 Методы вычисления интегралов. Формулы трапеций и Симпсона

Для приближенного вычисления интегралов существует много разных методов. Пусть надо найти:

m

I y(x) dx ?

n

101

Для вычисления интеграла Мора часто используют метод Верещагина. Однако более удобными являются приближенные методы.

Рис. 16.5

их четыре). Поскольку по геометрическому смыслу интеграл представляет собой площадь фигуры mnkl, то С можно вычислить приближенно, представив ее в виде суммы площадей четырех трапеций:

При этом в отличие от метода трапеций, отрезок а должен разбиваться

16.2. Вычисление прогибов на основе решения дифференциального уравнения изогнутой оси балки

Прогибы можно находить и другими способами, например, на основе решения дифференциального уравнения изогнутой оси балки. Для вывода этого уравнения, рассмотрим элемент балки (рис.16.6).

102

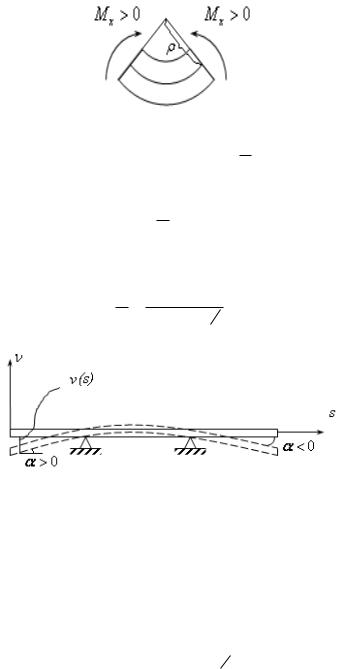
Рис.16.7

Очевидно, что k зависит от геометрии сечения и материала балки. Найдем эту зависимость.

Рассмотрим малый элемент балки длины ds (рис. 16.8). После изгиба он превратится в изогнутый элемент. Длина волокна BC, которое проходит через центр тяжести сечения, не изменяется и будет равна ds . Нижнее волокно DH удлиняется на величину, которое обозначим через .

103

Рис.16.8

Используя закон Гука и формулу Навье получаем

Отсюда получаем:

16.2.1. Решение дифференциального уравнения изогнутой оси балки

Если балка имеет постоянную толщину, то есть Jx const , то решение легко записывается в общем виде:

104

Хотя решение получено в общем виде, однако основная трудность заключается в определении Мх и констант C и D, поскольку на разных участках балки M x разные, а значит C и D также разные (в частности, если

балка имеет три участка, то нужно определить 6 констант).

Однако существует способ интегрирования, который сводит все неизвестные только к двум константам (разработан Клебшом)

16.2.2. Правила Клебша

Правила Клебша сводятся к следующему.

1) M x выражаем через внешние силы, которые лежат только слева (или

только справа) от сечения.

2) Если погонная сила q не доходит до правого конца, то ее доводим до этого правого конца и уравновешиваем ее снизу (рис.16.9).

При выполнении этих условий все константы С на разных участках будут одинаковы. Аналогично будут одинаковы все константы D.

Справедливость этого утверждения доказывается непосредственной проверкой, то есть подстановкой решения в условия стыковки решения на границе участков. Рассмотрим, например, случай, приведенный на рис.16.10.

рис16.10

По правилам Клебша момент M x на участках (I), (II) запишем в виде:

(I): M x P s

(II): M x P s m0 (s a)0

Дифференциальные уравнения на участках:

105

Решение этих уравнений на участках (1), (2) имеет вид:

Отсюда видно, что при s = a получим равенство углов наклона и прогибов, вычисленных по разным формулам при любых С и D, т.е. условия гладкости изогнутой оси выполняются. Аналогично проверяются условия гладкости на границе участка, на которой заканчивается погонная сила q.

16.2.3Условия для определения С и D

1)Первый случай . Рассмотрим балку, лежащую на двух опорах

(см. рис.16.11).

Таким образом из (16.13), получаем систему уравнений для С и D.

Опять получили два уравнения для С и D.

106

Пример вычисления прогиба

Пусть необходимо вычислить прогиб в центре балки длины l, загруженной погонной силой q. Решим эту задачу двумя способами.

Ввиду симметричности схемы можно сразу найти реактивные силы – они будут равны ql/2. Тогда изгибающий момент в сечении на расстоянии s

Первый способ. Использование дифференциального уравнения изогнутой оси балки.

Нарисуем эпюру изгибающих моментов Мх(T) от единичной силы Т=1

(см. рис. 16.13).

Рассмотрим различные приближенные методы интегрирования. 1. Метод трапеций по 2-м участкам.

Метод дал ошибку в 17% 2. Метод трапеций по 4-м участкам.

107

Таким образом, метод Симпсона в этом примере дает точное решение.

16.2.4. Балки на упругом основании. Закон Винклера

Рассмотрим основание (грунт) Приложим к мерному стержню силу Р (рис.16.14), тогда осадка стержня v , будет тем больше, чем больше сила Р.

Рис.16.14

Запишем это утверждение аналитически:

R r

Рис.16.15

Ее равнодействующая должна быть равна Р, т.е.

108

16.4. Уравнение изогнутой оси балки на упругом основании

Рассмотрим балку, которая лежит на грунте.

q

r

Рис.16.16

Такой моделью описывается поведение ленточных фундаментов, дорожных полотен, обшивок трехслойных панелей типа сэндвич.

Грунт противодействует внешним силам некоторой погонной силой r . Выразим ее через прогиб (s) . Для этого вырежем малый элемент (см. рис.16.16). Сравнивая рис.16.14 и рис.16.16 видим, что элемент балки, фактически представляет собой мерный стержень, для которого реакция определяется по формуле (16.16), т.е. реакция балки с прогибом связана соотношением:

Далее запишем уравнения равновесия элемента балки и уравнение ее изогнутой оси

109

Подставим (16.18) в (16.20):

2 M x qвнешн k v .s2

Подставляя сюда (16.19) получаем искомое уравнение:

Решение запишем в виде суммы:

Простой подстановкой в (16.21) можно проверить, что решение имеет вид:

Остальные константы получают из геометрических соображений (условий закрепления) и условий статики на концах балки.

16.5. Бесконечная балка на упругом основании

погонный вес полотна. Мы можем общее решение представить как сумму

сечения. Слева и справа прогиб симметричный, поэтому исследуем прогиб v только справа, то есть, найдем функцию v(s).

Рис.16.17

110