Предельные точки последовательности. (Два определения и их эквивалентность)
Определение 1.Числоaназывается предельной точкой последовательности {xn}, если из последовательности {xn} можно выделить подпоследовательность, сходящуюся кa.
Определение 2.Числоaназывается предельной точкой последовательности {xn}, если в любой-окрестности точкиaсодержится бесконечно много членов последовательности {xn}.
Утверждение. Определения 1 и 2 эквивалентны.
В самом деле, пусть a- предельная точка последовательности
{xn}
по первому определению, тогда существует
подпоследовательность
a, и в любой-окрестности
точкиaсодержится
бесконечно много членов последовательности
{xn},
а это и означает, что точкаaявляется предельной точкой последовательности
по определению 2.
Пусть {xn}
- числовая последовательность, и пустьk1 ,k2, … ,kn, … - возрастающая последовательность,
элементами которой являются натуральные
числа. Выберем из последовательности
{xn}
элементы с номерамиk1
,k2, … ,kn, … , получим вот такую последовательность:
,
она называется подпоследовательностью
последовательности {xn}.
Отметим, чтоknn.
Примеры подпоследовательностей:
{x2n} =x2,x4, … ,x2n, …
=x1,x3,x7,x13, …{xn} - сама последовательность.
Эквивалентность определений предела функции в точке по Коши и по Гейне.
Определение предела функции по Коши: пустьf(x) определена на множествеX, иa- предельная точкаX. Числоbназывается пределомf(x) приx a, если> 0> 0 такое, чтоx{0 <x-a<}:f(x) -b<.
Определение предела функции в точке a по Гейне:
b называется пределомf(x) приxa, если{xn}a(xna): {f(xn)}b.
[13] Сформулировать отрицание определения предела по Гейне.
Теорема 6.5.Определения предела функции в точке a по Гейне и по Коши эквивалентны.
Доказательство.
Пусть
f(x)
=bпо Коши. (1)
Требуется доказать, что {xn}a(xna) соответствующая последовательность {f(xn)}b, то есть> 0N,n>N:f(xn) -b<. (2). Рассмотрим произвольную последовательность {xn}a(xna). Возьмем> 0. В силу условия (1)> 0,
x {0 <x-a<}:f(x) -b<. (3). В свою очередь, так как {xn}a(xna), то для указанногоN,n>N: 0 <xn-a<(4). Из (4) и (3) следует, чтоn>N:f(xn) -b<, то есть выполнено условие (2),что и требовалось доказать.
2. Пусть
f(x)
=bпо Гейне. (5)
Предположим, что
f(x)bпо Коши. Тогда>
0 такое, что>
0x{0 <x-a<}:f(x)
-b.
Возьмем какую-нибудь последовательность
{n}+0
(n> 0). Например, можно взятьn=
.
Согласно сказанному выше,
n
xn
:f(xn)
- b
. (7)
Из (6) следует, что {xn}a(xna).
Отсюда в силу условия (5) следует, что
{f(xn)}b,
и поэтому
=
0. С другой стороны, в силу неравенства
(7)
> 0. Полученное
противоречие доказывает, что наше
предположение неверно и, следовательно,
f(x)
=bпо Коши.
Теорема доказана.
Примеры.
Докажем, что
sin
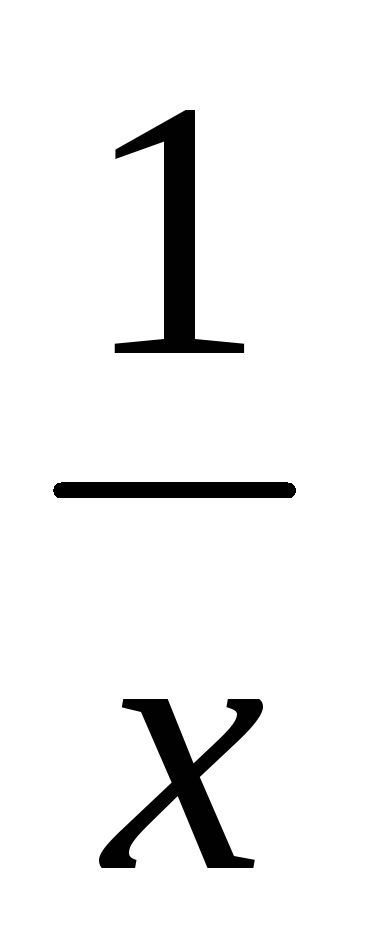не существует (по Гейне).
{xn}
=
0. {f(xn)}
=
1.
{x'n}
=
0. {f(x'n)}
=
-1.
Отсюда следует, согласно определению
предела функции по Гейне, что
sin
не существует.
Критерий Коши существования предела функции в точке.
Определение: Пустьa- предельная точка области определенияf(x). Говорят, что функцияf(x) удовл. в точкеaусловию Коши, если> 0> 0,x' иx'', 0 <x' -a<, 0 <x''-a<:
f(x') -f(x'')<.
Условие Коши для функции аналогично условию фундаментальности последовательности.
Теорема 6.6.(Критерий Коши) Для того, чтобы функция имела предел в точкеa, необходимо и достаточно, чтобы она удовлетворяла в этой точке условию Коши.
Доказательство.
Необходимость. Дано:
f(x)
=b. Требуется доказать:f(x)
удовлетворяет в точкеaусловию Коши. Зададим произвольное> 0. Согласно определению предела
функции по Коши,
> 0,
x'
{0 <x'
- a
< },
f(x')
- b
< 
,
и
> 0,
x''
{0 <x''
- a
< },
f(x'')
- b
< 
.
Отсюда следует, что x' {0 <x' - a < } и x'' {0 <x'' - a < }: f(x') - f(x'')=
= ( f(x')
-b) - (f(x'')
-b)
+
<.А это и означает, чтоf(x)
удовлетворяет в точкеaусловию Коши.
Необходимость доказана.
Достаточность.Дано:f(x) удовлетворяет в точкеaусловию Коши. Требуется доказать:
f(x).
Согласно определению предела функции
по Гейне, нужно доказать, что{xn}a(xn
a) {f(xn)}
сход., причем сходится к одному и тому
же числу для всех {xn}a(xn
a). Рассмотрим
произвольную последовательность {xn}a(xn
a). Докажем сначала,
что последовательность {f(xn)}
- фундаментальная. Зададим произвольное> 0. Согласно
условию (1),> 0,x'
иx'', 0 <x'
-a<, 0 <x''-a<:
f(x')
-f(x'')<. (2). В свою
очередь, так как {xn}aиxn
a, тоN,n>N:
0 <xn-a<,m>N:
0 <xm-a<. (3). Из (2) и (3) следует,
чтоn>Nиm>N:f(xn)
-f(xm)<. А это и означает
по определению, что последовательность
{f(xn)}
- фундаментальная. Следовательно, она
сходится. Итак, мы доказали, что{xn}a(xn
a): {f(xn)}
сходится. Остается доказать, что для
всех таких последовательностей {xn}:
{f(xn)}
сходится к одному и тому же числу. Пусть
для {xn}a(xn
a): {f(xn)}b,
а для {xn'}a(xn'
a): {f(xn')}b'.
Нужно доказать, чтоb'
=b. Составим посл.
{xn''}
=x1, x1'
, x2, x2'
, … , xn, xn''
, …
{xn''} a (xn'' a).
Согласно доказанному, {f(xn'')}b'', но {f(xn)} и {f(xn')} - подпоследовательности последовательности {f(xn'')}, следовательно, эти последовательности сходятся кb'', а это и означает, чтоb=b' =b'', что и требовалось доказать.
Теорема доказана.