
- •Теорема о пределе монотонной ограниченной функции.
- •Теорема 2.7
- •Устойчивость знака непрерывной функции.
- •Теорема 3.4
- •Непрерывность сложной функции.
- •Теорема 3.3
- •Теорема о существовании, строгой монотонности и непрерывности обратной функции.
- •Теорема 3.5
- •Достаточное условие непрерывности функции в точке.
- •Теорема 3.1
- •Производная обратной функции.
- •Производная сложной функции.
- •Производная функции, заданной параметрически.
- •Формула Лейбница.
- •Замена переменной в неопределенном интеграле.
- •Интегрирование по частям в неопределенном интеграле.
- •Теорема о стягивающейся системе сегментов.
- •Теорема Больцано-Вейрштрасса.
- •Критерий Коши сходимости последовательности.
- •Предельные точки последовательности. (Два определения и их эквивалентность)
- •Эквивалентность определений предела функции в точке по Коши и по Гейне.
- •Критерий Коши существования предела функции в точке.
- •Ограниченность непрерывной на сегменте функции (1-ая теорема Вейрштрасса).
- •Точки локального экстремума функции. Необходимое условие экстремума.
- •Теорема Ролля.
- •Формула Лагранжа.
- •Формула Коши.
- •Многочлен Тейлора. Формула Тейлора с остаточным членом в форме Пеано.
- •2. Формула Тейлора с остаточным членом в форме Пеано.
- •Формула Тейлора с остаточным членом в форме Лагранжа.
Непрерывность сложной функции.
Непрерывность сложной функции.
Пусть аргумент tфункцииy=f(t) является функцией аргументаx:t=(x). В этом случае говорят, что переменнаяуявляется сложной функцией от аргументахили у является суперпозицией функцийfи.
y=f((x)).
Пример:
y=sin(![]() )
- сложная функция.
)
- сложная функция.
y=sint,
гдеt=![]() .
.
Теорема 3.3
Если t=(x) непрерывна в точкеа(а) =b, и функцияf(t) непрерывна в точкеb, то сложная функцияf((x)) непрерывна в точкеа.
Доказательство:
По определению непрерывности нужно доказать, что > 0> 0: |f((x)) -f((a)) | <при
| x-a| <.
Зададим произвольное > 0.
Так как f(t) непрерывна в точкеb, то> 0: |f(t) -f(b) | <при |t-b| <. Отсюда следует, что
| f((x)) -f((a)) | <при |(x) -(a) | <.(1)
В свою очередь, так как (x) непрерывна в точкеa,
то для указанного > 0: |(x) -(a) | <при |x-a| <.(2)
Из (1)и(2)следует, что |f((x)) -f((a)) | <, если |x-a| <, что и требовалось доказать.
Теорема доказана.
Теорема о существовании, строгой монотонности и непрерывности обратной функции.
П![]() усть
функцияу=f(x)
определена на множествеХ, и пустьY- множество её
значений. Пусть каждое своё значение
функция принимает только в одной точке.
В таком случае говорят, что функцияу=f(x)
осуществляет взаимно однозначное
отображение множестваХна множествоY. Поставим в соответствие
каждомууYто числохХ,
для которогоf(x)
=у. Тем самым на множествеYбудет определена функция. Она называется
обратной по отношению к функцииу=f(x)
и обозначаетсях=
усть
функцияу=f(x)
определена на множествеХ, и пустьY- множество её
значений. Пусть каждое своё значение
функция принимает только в одной точке.
В таком случае говорят, что функцияу=f(x)
осуществляет взаимно однозначное
отображение множестваХна множествоY. Поставим в соответствие
каждомууYто числохХ,
для которогоf(x)
=у. Тем самым на множествеYбудет определена функция. Она называется
обратной по отношению к функцииу=f(x)
и обозначаетсях=![]() (у).
Отметим, что обратной для функциих=
(у).
Отметим, что обратной для функциих=![]() (у)
является функцияy=f(x),
поэтому функцииy=f(x)
их=
(у)
является функцияy=f(x),
поэтому функцииy=f(x)
их=![]() (x)
называются взаимно обратными.
(x)
называются взаимно обратными.
Примеры.
1) y=![]() ,X= [0, +),
,X= [0, +),
x=![]() ,Y= [0, +).
,Y= [0, +).
(рисунок)
2) y=![]() ,X= (-,).
,X= (-,).
Эта функция обратной не имеет.
(рисунок)
Теорема 3.5
Пусть функция y=f(x) определена, непрерывна и строго монотонна на [a,b].
Тогда множеством её значений является
сегмент Y= [f(a),f(b)],
на сегментеYсуществует
обратная функциях=![]() (
(![]() у),
строго монотонная и непрерывная.
у),
строго монотонная и непрерывная.
Доказательство.
(рисунок)
Пусть y=f(x) возрастает на [a,b].
В силу следствия из теоремы 3.4функцияy=f(x) принимает любое значение междуf(a) иf(b), а так какy=f(x)-ворастающая функция, то у неё нет значений, меньшихf(a), и значений, большихf(b). Тем самым, множество её значенийY= [f(a),f(b)].
Так как y=f(x)- возрастающая функция, то каждое значениеyYфункция принимает только в одной точке. Отсюда следует, что на сегментеYсуществует обратная функциях=
 (
( у).
у).Докажем, что х=
 (у)возрастает
на сегментеY.
(у)возрастает
на сегментеY.
Возьмём
![]() и
и
![]() Y,
Y,
![]() <
<![]() Требуется доказать, что
Требуется доказать, что![]() <
<![]() ,
,
То есть, что
![]() <
<![]() .
Так какf(
.
Так какf(![]() )
=
)
=![]() ,f(
,f(![]() )
=
)
=
![]() ,
то если предположить, что
,
то если предположить, что![]()
![]() ,
в силу возрастания функцииf(x)
получимf(
,
в силу возрастания функцииf(x)
получимf(![]() )f(
)f(![]() ),
то есть
),
то есть![]()
![]() ,
что противоречит неравенству
,
что противоречит неравенству
![]() <
<![]() .
Таким образом
.
Таким образом![]() (
(![]() )
<
)
<![]() (
(![]() ),
то есть обратная функция возрастает на
сегментеY.
),
то есть обратная функция возрастает на
сегментеY.
Остаётся доказать непрерывность обратной функции на сегменте Y.
Возьмём произвольную точку
![]() (f(a),f(b))
и докажем непрерывность обратной функции
в точке
(f(a),f(b))
и докажем непрерывность обратной функции
в точке
![]() .
Непрерывность в точкахf(a)
иf(b)
доказывается аналогично.
.
Непрерывность в точкахf(a)
иf(b)
доказывается аналогично.
(рисунок)
По определению непрерывности нужно
доказать, что > 0> 0: |
![]() (y)
-
(y)
-
![]() (
(![]() )
| <
)
| <
при | y-
![]() | <,
или |
| <,
или |![]() (y)
-
(y)
-
![]() |
<при |y-
|
<при |y-
![]() | <.
Иначе говоря, нужно доказать, что значения
обратной функции лежат в- окрестности точки
| <.
Иначе говоря, нужно доказать, что значения
обратной функции лежат в- окрестности точки
![]() для
значений аргументауиз- окрестности точки
для
значений аргументауиз- окрестности точки![]() .
.
Возьмем произвольное > 0 столь малым, чтобы
![]() -и
-и
![]() +[a,b].
Пусть
+[a,b].
Пусть
f(![]() -) =
-) =![]() ,f(
,f(![]() +) =
+) =![]() .
Так как функцияy=f(x)
- возрастающая, то
.
Так как функцияy=f(x)
- возрастающая, то
![]() <
<![]() <
<![]() .
А так как обратная функцияx=
.
А так как обратная функцияx=![]() (y)
также возрастающая, то
(y)
также возрастающая, то![]() <
<![]() (y)
<
(y)
<![]() при
при
![]() <y<
<y<![]() ,
то есть значения обратной функции лежат
в-
окрестности точки
,
то есть значения обратной функции лежат
в-
окрестности точки![]() для значений аргументаy(
для значений аргументаy(![]() ,
,![]() ).
).
Возьмём - окрестность
точки![]() ,
принадлежащую интервалу (
,
принадлежащую интервалу (![]() ,
,![]() ).
Тогда, согласно доказанному, значения
обратной функции для значений аргументаyиз этой- окрестности лежат в- окрестности точки
).
Тогда, согласно доказанному, значения
обратной функции для значений аргументаyиз этой- окрестности лежат в- окрестности точки![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Теорема доказана.
Доказать, что

 = 1 (первый замечательный предел).
= 1 (первый замечательный предел).
![]()
![]() = 1 (первый замечательный предел).
= 1 (первый замечательный предел).
Доказательство:
sinx<x<tgxпри 0 <x<
![]() .
Разделив наsinx,
получим 1 <
.
Разделив наsinx,
получим 1 <
![]() <
<
![]() .
Отсюдаcosx<
.
Отсюдаcosx<
![]() < 1 при 0 <x<
< 1 при 0 <x<
![]() .
Входящие в эти неравенства функции -
чётные, поэтому эти неравенства верны
также при -
.
Входящие в эти неравенства функции -
чётные, поэтому эти неравенства верны
также при -![]() <x< 0. Приx0cosx1, так как сosx- непрерывная функция. Следовательно,
по теореме о двух милиционерах
<x< 0. Приx0cosx1, так как сosx- непрерывная функция. Следовательно,
по теореме о двух милиционерах
![]() 1 прих0, что и требовалось доказать.
1 прих0, что и требовалось доказать.
Теорема доказана.
Следствие 1.
sinx=x+ о(х) прих0. В самом деле, так как
![]()
![]() = 1, тоsinx~x
= 1, тоsinx~x
при х0, и ,следовательноsinx-x=o(x), откудаsinx=x+ о(х) прих0:
(рисунок)
Следствие 2.
cosx= 1
-
![]() +o(x2)
прих0.
+o(x2)
прих0.
Доказательство:
![]()
![]() =
=![]()
![]() =
=![]()
![]() =
1. Отсюда следует, что
=
1. Отсюда следует, что
1 - cos~
![]() прих0, поэтому 1 -cosx-
прих0, поэтому 1 -cosx-![]() =o(x2)
прих0, или
=o(x2)
прих0, или
cosx= 1
-
![]() +o(x2)
прих0.
+o(x2)
прих0.
Следствие 3.
tgx=x+o(x) прих0.
Примеры:

 =
=
 =
=

 =12.
=12.
2)
![]()
![]() ;
;
1) первая попытка:
![]() =
=![]() =
=![]() -
чему равен предел этой дроби, сказать
нельзя.
-
чему равен предел этой дроби, сказать
нельзя.
2) вторая попытка:
![]()
![]()

![]()

![]()
![]() .
.
Доказать, что
 (1
+х)1/х =е. (второй замечательный предел.
(1
+х)1/х =е. (второй замечательный предел.
![]() (1
+х)1/х =е.(это неопределённость типа 1).
(1
+х)1/х =е.(это неопределённость типа 1).
Доказательство:
По определению, е =
![]()
![]() .
.
Неверное доказательство теоремы:
Положим![]() =х, тогда
=х, тогда![]() =
(1 +х)1/х , иx0 приn.
=
(1 +х)1/х , иx0 приn.
Поэтому (1 + х)1/хeприх.
Это доказательство неверно, так как здесь x0 определённым способом
(x=
![]() ,
гдеn- натуральное
число), а нужно рассматривать произвольное
стремлениеxк нулю.
,
гдеn- натуральное
число), а нужно рассматривать произвольное
стремлениеxк нулю.
Верное доказательство.
Введём функцию f(x)
=
![]() (x1).
(x1).
При nx<n+ 1:f(x)
=
![]() ,
поэтому
,
поэтому
![]() f(x)
=e.
f(x)
=e.
Воспользуемся неравенствами: [x]x< [x+1] = [x] + 1. Отсюда приx1 имеем:
![]() <
<![]()
![]() а,
следовательно, 1 +
а,
следовательно, 1 +
![]() <
1+
<
1+![]() 1 +
1 +![]() .
.
Поэтому
![]()
![]()
![]() или
или


![]()

![]()
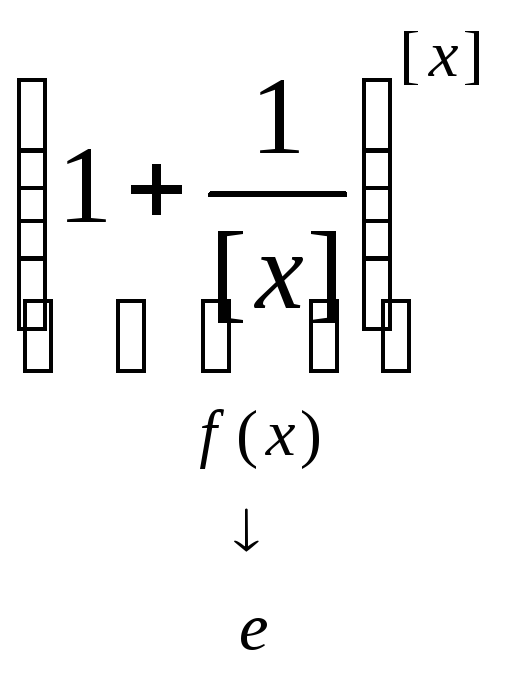
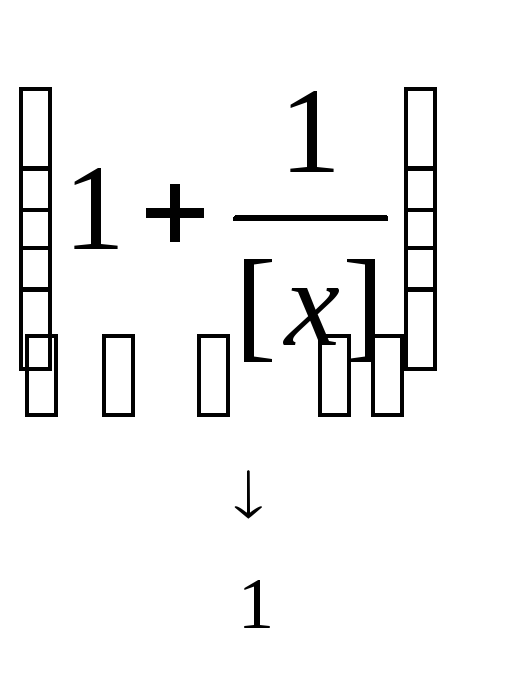 .
.
Отсюда следует, что
![]()
![]() =е.
=е.
Положим у=
![]() .
Тогдаy+0, еслих+и
мы получаем,
.
Тогдаy+0, еслих+и
мы получаем,
что
![]() (1
+у)1/у=еили
(1
+у)1/у=еили
![]() (1
+х)1/х=е.(1)
(1
+х)1/х=е.(1)
Рассмотрим теперь
![]() (1
+х)1/х. Положиму= -х. Тогдаy+0, если х-0.
(1
+х)1/х. Положиму= -х. Тогдаy+0, если х-0.
(1 + х)1/х= (1 -у)-1/у=![]() =
=![]() .
.
Положим
![]() =z. Тогдаz+0,
еслиy+0 иy=
=z. Тогдаz+0,
еслиy+0 иy=
![]() ,
,![]() =
=![]() +1.
+1.
Таким образом, (1 + х)1/х=![]() =(1
+z)1/z+1.
Еслих-0, тоz+0, поэтому
=(1
+z)1/z+1.
Еслих-0, тоz+0, поэтому
(1 + z)1/z+1=

![]() e.
e.
Итак,
![]() (1 +х)1/х =е.(2)
(1 +х)1/х =е.(2)
Из (1)и(2)следует, что
![]() (1 +х)1/х =е.
(1 +х)1/х =е.
Теорема доказана.
Примеры:

 =
=
 loga[(1+x)1/x]
=loga
e=
loga[(1+x)1/x]
=loga
e=
 ,
так как (1+x)1/x
eприx0.
,
так как (1+x)1/x
eприx0.
Отсюда следует, что loga(1+x)
~
![]() прих0.
прих0.
Поэтому loga(1+x)
-
![]() =о(х) прих0, то естьloga(1+x)
=
=о(х) прих0, то естьloga(1+x)
=
![]() +о(х) прих0. В частности, еслиа=е, то
получаемln(1+x)
=х+о(х). 2)
+о(х) прих0. В частности, еслиа=е, то
получаемln(1+x)
=х+о(х). 2)
![]()
![]() .
Обозначимах- 1 =у.
Тогдаy0 прих0,х=loga(1+x).
.
Обозначимах- 1 =у.
Тогдаy0 прих0,х=loga(1+x).
![]() =
=![]() =
=
![]()
![]()
![]() =lna, так
как (1 +y)1/y еприy0. Итак,
=lna, так
как (1 +y)1/y еприy0. Итак,
![]()
![]() =lna.
Отсюда следует, чтоах- 1
~xlnaприх0.
=lna.
Отсюда следует, чтоах- 1
~xlnaприх0.
Поэтому ах=1 +xlna+o(x) прих0, в частности,ех=1 +x+o(x).
