
- •Теорема о пределе монотонной ограниченной функции.
- •Теорема 2.7
- •Устойчивость знака непрерывной функции.
- •Теорема 3.4
- •Непрерывность сложной функции.
- •Теорема 3.3
- •Теорема о существовании, строгой монотонности и непрерывности обратной функции.
- •Теорема 3.5
- •Достаточное условие непрерывности функции в точке.
- •Теорема 3.1
- •Производная обратной функции.
- •Производная сложной функции.
- •Производная функции, заданной параметрически.
- •Формула Лейбница.
- •Замена переменной в неопределенном интеграле.
- •Интегрирование по частям в неопределенном интеграле.
- •Теорема о стягивающейся системе сегментов.
- •Теорема Больцано-Вейрштрасса.
- •Критерий Коши сходимости последовательности.
- •Предельные точки последовательности. (Два определения и их эквивалентность)
- •Эквивалентность определений предела функции в точке по Коши и по Гейне.
- •Критерий Коши существования предела функции в точке.
- •Ограниченность непрерывной на сегменте функции (1-ая теорема Вейрштрасса).
- •Точки локального экстремума функции. Необходимое условие экстремума.
- •Теорема Ролля.
- •Формула Лагранжа.
- •Формула Коши.
- •Многочлен Тейлора. Формула Тейлора с остаточным членом в форме Пеано.
- •2. Формула Тейлора с остаточным членом в форме Пеано.
- •Формула Тейлора с остаточным членом в форме Лагранжа.
Замена переменной в неопределенном интеграле.
Замена переменной.
Теорема 5.2.Пусть функцияx=(t) определена и дифференцируема на промежуткеT, и пусть промежутокX- множество ее значений. Пустьf(x) определена наXи имеет первообразнуюF(x).
Тогда F((t)) - первообразная дляf((t)'(t) наT.
Доказательство.
tT :F((t))'
=
![]() '(t)
=f((t)'(t).
'(t)
=f((t)'(t).
Теорема доказана.
Следствие.![]() =
F((t))
+С.
=
F((t))
+С.
F((t))
+С=
![]() =
=
![]() .
.
Таким образом,
![]() =
=![]() -- формула замены переменной в
неопределенном интеграле.
-- формула замены переменной в
неопределенном интеграле.
Примеры:
 = [x =
= [x =
 ,dx=
,dx= dt] =
dt] =

 =
=
 (-cost+C)
=
(-cost+C)
=
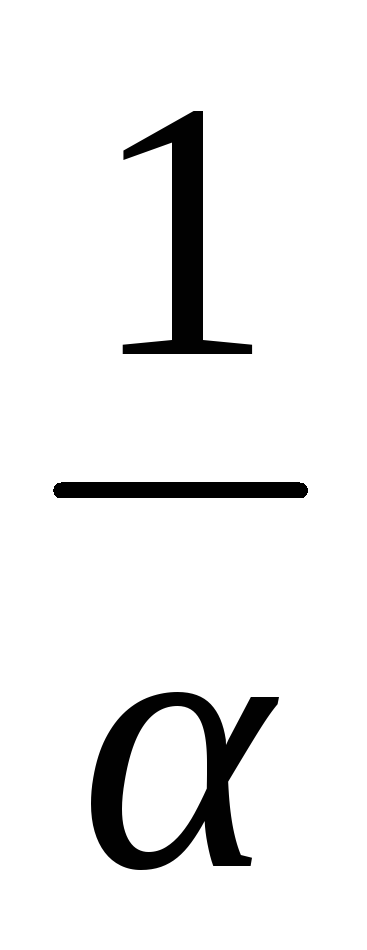 cosx+C.
cosx+C. ,
(a> 0)
,
(a> 0)
Подынтегральная функция определена для 0 x a.
x = asin2t
(asin2t
(t)),
0
t
![]() ,dx = 2asintcostdt
,dx = 2asintcostdt
sint =
![]() ,t =
arcsin
,t =
arcsin![]() ,
cost =
,
cost =
![]() .
.
![]() =
=
![]() 2asintcostdt
= 2a
2asintcostdt
= 2a![]() = 2a
= 2a![]() =
=
=a(t
- 1/2sin2t)
+ C = a(t
-sintcost)
+ C = a
arcsin![]() -
-![]() +C.
+C.
Интегрирование по частям в неопределенном интеграле.
Интегрирование по частям.
Теорема 5.3.Пустьu(x)
иv(x)
определены и дифференцируемы на
промежуткеX, и пусть
функцияu(x)
иv'(x)
имеет первообразную на промежуткеХ,
то есть существует![]() .
Тогдаu(x)v'(x)
также имеет первообразную на промежуткеХ, и спараведлива формула:
.
Тогдаu(x)v'(x)
также имеет первообразную на промежуткеХ, и спараведлива формула:
![]() =u(x)v(x)
-
=u(x)v(x)
-![]() -
формула интегрирования по частям.
-
формула интегрирования по частям.
Доказательство: Воспользуемся
формулой: (uv)' =u'v
+ uv' ,vu'
= (uv)' -uv'.uv' имеет первообразную
по условию теоремы. (uv)'
имеет первообразнуюuv.
Следовательно иvu'имеет первообразную и справедливо
равенство:![]() =uv-
=uv-![]() .
.
Теорема доказана.
Следствие: Так какu'dx=du,v'dx=dv, то формулу интегрирования по частям можно записать в виде:
![]() =uv -
=uv -![]() .
.
Пример:
![]() =
=![]() =[v
= x2,
dex]
= x2ex
-
=[v
= x2,
dex]
= x2ex
-
![]() =x2ex
- 2
=x2ex
- 2
![]() =x2ex
- 2(xex
-
=x2ex
- 2(xex
-![]() )
=
)
=
= ex (x2 - 2x + 2) + C.
Некоторые интегралы не выражаются через
элементарные функции, например:
![]() ,
то есть, класс элементарных функций не
замкнут относительно операции
интегрирования.
,
то есть, класс элементарных функций не
замкнут относительно операции
интегрирования.
Теорема о стягивающейся системе сегментов.
Пусть дана последовательность сегментов [a1 ,b1], [a2 ,b2], … , [an,bn], … - такая, что каждый следующий сегмент содержится в предыдущем.
(здесь рисунок)
n: an an+1<bn+1bn, (1)
и пусть длина n-го сегментаbn -an0 приn . Такую последовательность сегментов назовем стягивающейся системой сегментов.
Теорема 6.1. Существует, и притом только одна, точка, принадлежащая всем сегментам стягивающейся системы.
Доказательство: Из неравенств (1) следует: {an} - неубывающая последовательность, {bn} - невозрастающая. Кроме того, обе эти последовательности ограничены, так как все их члены лежат на сегменте [a,b]. Следовательно, эти последовательности сходятся. Так какbn -an0 приn , эти последовательности имеют один и тот же предел.liman=limbn=c. Так как {an} - неубывающая последовательность,an<c(n).n:an c bn , то естьc[an,bn]n. Существование точки, принадлежащей всем сегментам стягивающейся системы, доказано. Докажем теперь, что такая точка только одна. Предположим, существует другая точкаd[an,bn]n. Пусть для определенностиd>c.
(здесь рисунок)
Но в этом случае bn-and-c> 0,lim(bn-an) =d-c> 0, что противоречит условиюlim(bn-an) = 0. Итак, точкас- единственная, принадлежащая всем сегментам стягивающейся системы.
Теорема доказана.
Эта теорема выражает свойство, которое называется непрерывностью множества вещественных чисел. Множество рациональных чисел этим свойством не обладает.
