
- •Теорема о пределе монотонной ограниченной функции.
- •Теорема 2.7
- •Устойчивость знака непрерывной функции.
- •Теорема 3.4
- •Непрерывность сложной функции.
- •Теорема 3.3
- •Теорема о существовании, строгой монотонности и непрерывности обратной функции.
- •Теорема 3.5
- •Достаточное условие непрерывности функции в точке.
- •Теорема 3.1
- •Производная обратной функции.
- •Производная сложной функции.
- •Производная функции, заданной параметрически.
- •Формула Лейбница.
- •Замена переменной в неопределенном интеграле.
- •Интегрирование по частям в неопределенном интеграле.
- •Теорема о стягивающейся системе сегментов.
- •Теорема Больцано-Вейрштрасса.
- •Критерий Коши сходимости последовательности.
- •Предельные точки последовательности. (Два определения и их эквивалентность)
- •Эквивалентность определений предела функции в точке по Коши и по Гейне.
- •Критерий Коши существования предела функции в точке.
- •Ограниченность непрерывной на сегменте функции (1-ая теорема Вейрштрасса).
- •Точки локального экстремума функции. Необходимое условие экстремума.
- •Теорема Ролля.
- •Формула Лагранжа.
- •Формула Коши.
- •Многочлен Тейлора. Формула Тейлора с остаточным членом в форме Пеано.
- •2. Формула Тейлора с остаточным членом в форме Пеано.
- •Формула Тейлора с остаточным членом в форме Лагранжа.
Теорема Больцано-Вейрштрасса.
Теорема 6.2.(Больцано-Вейерштрасса). Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Доказательство: Пусть {xn} - ограниченная последовательность, то есть все ее элементы лежат на некотором сегменте [a ,b].
a xnb(n).
(здесь рисунок)
Разделим сегмент [a
,b] пополам. По
крайней мере на одной из половин сегмента
[a ,b]
лежит бесконечно много членов
последовательности {xn},
обозначим эту половину через [a1
,b1]. Возьмем
какой-нибудь
![]() :a1
:a1 ![]() b1. Далее разделим
сегмент [a1
,b1] пополам
и обозначим через [a2
,b2] ту
половину, на которой находится бесконечно
много членов последовательности {xn}.
Выберем
b1. Далее разделим
сегмент [a1
,b1] пополам
и обозначим через [a2
,b2] ту
половину, на которой находится бесконечно
много членов последовательности {xn}.
Выберем![]() [a2 ,b2],k2>k1.a2
[a2 ,b2],k2>k1.a2
![]() b2. Затем разделим
сегмент [a2
,b2] пополам,
и так далее. Продолжая этот процесс,
получим стягивающуюся систему сегментов
[a1 ,b1], [a2
,b2], … , [an,bn],
… (так какbn-an=
b2. Затем разделим
сегмент [a2
,b2] пополам,
и так далее. Продолжая этот процесс,
получим стягивающуюся систему сегментов
[a1 ,b1], [a2
,b2], … , [an,bn],
… (так какbn-an=
![]() 0 приn), и
последовательность
0 приn), и
последовательность
![]() ,
которая является подпоследовательностью
последовательности {xn}.
,
которая является подпоследовательностью
последовательности {xn}.
n: an
![]()
bn. (1)
bn. (1)
По теореме 6.1 (Теорема 6.1. Существует,
и притом только одна, точка, принадлежащая
всем сегментам стягивающейся системы)точкас:liman=limbn=c. Отсюда и из
неравенства (1) следует, что
![]() cприn
.
Таким образом, мы выделили из
последовательности {xn}
сходящуюся подпоследовательность.
cприn
.
Таким образом, мы выделили из
последовательности {xn}
сходящуюся подпоследовательность.
Теорема доказана.
Определение. Последовательность {xn} называется неограниченной, еслиA > 0n:xn>A.
//Замечание: Для неограниченных последовательностей теорема Больцано-Вейерштрасса неверна.
Примеры.
{n} = 1, 2, 3, …,n, …
Из {n} нельзя выделить сходящуюся подпоследовательность.
{xn} = 1, 0, 2, 0, 3, 0, … ,n, 0, …
{xn} - неограниченная подпоследовательность.
{x2n}0.
Критерий Коши сходимости последовательности.
Определение:Последовательность {xn} называется фундаментальной, если> 0N,n>Nинатуральногоp:xn+p-xn<.
Так как m=n+p- тоже произвольное число >N, то определение фундаментальности можно сформулировать следующим образом:> 0N,n>Nиm>N:xm-xn<.
Геометрически фундаментальность последовательности {xn} означает, что для любого сколь угодно малогосуществует такой номерN, что любые два члена последовательности с большим, чемN, номерами, отстоят друг от друга не более, чем на.
(здесь рисунок)
Пример: Докажем, что последовательность
![]() =1,
=1,![]() ,
,![]() ,
… - фундаментальная. Зададим произвольное> 0, возьмемN>
,
… - фундаментальная. Зададим произвольное> 0, возьмемN>
![]() .
Тогда
.
Тогда![]() >, иn>Nинатуральногоp:xn+p-xn=
>, иn>Nинатуральногоp:xn+p-xn=
![]() =
=![]() -
-![]() <
<
![]() <
<![]() <. Это и означает,
что последовательность
<. Это и означает,
что последовательность![]() -
фундаментальная.
-
фундаментальная.
Лемма 2. Фундаментальная последовательность ограничена.
Доказательство: Пусть {xn}
- фундаментальная последовательность.
Возьмем какое-нибудь положительное,
например,= 1. По
определению фундаментальности,N,n>Nиm>N:xm-xn< 1. Зафиксируем какое-нибудьm0>N, тогда![]() <
1 приn>N,
или
<
1 приn>N,
или
![]() -
1 <xn<
-
1 <xn<
![]() +
1 приn>N.
Таким образом, все члены последовательности
с номерамиn>Nлежат в интервале (
+
1 приn>N.
Таким образом, все члены последовательности
с номерамиn>Nлежат в интервале (![]() -
1,
-
1,
![]() +
1), вне этого интервала лежит только
конечное число членов последовательности.
Это и означает, что последовательность
{xn}
ограничена.
+
1), вне этого интервала лежит только
конечное число членов последовательности.
Это и означает, что последовательность
{xn}
ограничена.
Лемма доказана.
Теорема 6.4(критерий Коши сходимости последовательности) Для того, чтобы числовая последовательность сходилась, необходимо и достаточно, чтобы она была фундаментальной.
Доказательство.
Необходимость. Дано: Последовательность {xn} сходится. Требуется доказать, что последовательность {xn} - фундаментальная. Пусть
 =a.
Зададим произв.> 0.
=a.
Зададим произв.> 0.
По определению предела, N,n>N:xn-a<
![]() ,
иm>N:xm-a<
,
иm>N:xm-a<
![]() .
Еслиn>N,m>N,
тоxm-xn=(xm-a)
- (xn-a)
.
Еслиn>N,m>N,
тоxm-xn=(xm-a)
- (xn-a)
 +
+ <.
<.
Это и означает по определению, что последовательность {xn} - фундаментальная.
Необходимость доказана.
Достаточность. Дано: Последовательность {xn} - фундаментальная. Требуется доказать: {xn} сходится. По лемме 2, последовательность {xn} ограничена, следовательно, можно выделить сходящуюся подпоследовательность
 .
Пусть
.
Пусть
 =a. Докажем, что
=a. Докажем, что
 =a. Зададим произвольное> 0. Так как
подпоследовательность
=a. Зададим произвольное> 0. Так как
подпоследовательность
 сходится кa, начиная
с некоторого номераN1все члены
сходится кa, начиная
с некоторого номераN1все члены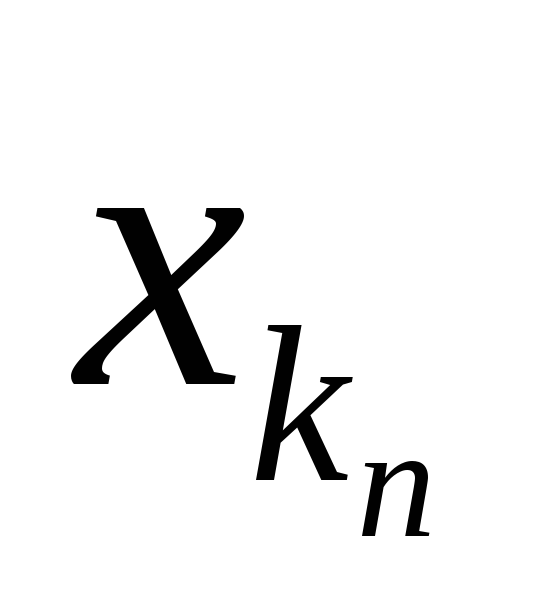 {
{ -
окрестности точкиa},
а так как последовательность {xn}
- фундаментальная, то начиная с некоторого
номераN2все
членыxnотстоят от членов
-
окрестности точкиa},
а так как последовательность {xn}
- фундаментальная, то начиная с некоторого
номераN2все
членыxnотстоят от членов меньше, чем на
меньше, чем на
 .
Следовательно, начиная с номераN=max(N1,
N2) все члены
последовательностиxn{-
окрестности точкиa},
а это и означает, что
.
Следовательно, начиная с номераN=max(N1,
N2) все члены
последовательностиxn{-
окрестности точкиa},
а это и означает, что
 =a, что и требовалось
доказать.
=a, что и требовалось
доказать.
Теорема доказана.
Пример: Рассмотрим последовательность {sinn}. Докажем, что эта последовательность расходится. Для этого достаточно доказать, что она не является фундаментальной. Предположим противное: допустим, что {sinn} - фундаментальная. Тогда если> 0N,n>Nинатуральногоp:xn+p-xn=sin(n+p) -sinn<. Возьмемp= 2.
sin(n+2) - sin n< 2sin 1cos(n+1)< .
> 0
N,
n >N:
cos(n+1)<
![]() .
.
=> {cosn} - бесконечно малая, то естьcosn0 приn.
cos(n+1) = cos ncos 1- sin nsin 1.
sin n
=
![]() (
cosncos
1 - cos(n+1))
0 при n
.
(
cosncos
1 - cos(n+1))
0 при n
.
cosnиsinn0 приn. Но это противоречит тому, чтоcos2n+sin2n=1.
Полученное противоречие доказывает, что последовательность {sinn} расходится.
