Литература.

Основная литература

1. Данко П. Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах.- М.

2. «Общий курс высшей математики для экономистов» под ред. В.И. Ермакова. – М. «Индра-М», 2002.

3. Турецкий В.Я. Математика и информатика. – М.: ИНФРА-М, 2005.

4. Шипачев В.С. Высшая математика.- М., Высшая школа, 2005.

5. Шипачев В.С. Сборник задач по высшей математике – М. Высшая школа, 2004

Дополнительная литература

6. Выгодский М.Я. Справочник по высшей математике.

7. Красс М.С. Чупрынов Б.П. Математика для экономистов.- Спб.: Питер, 2007.

8. Лунгу К.Н., Письменный Д.Т. и др. Сборник задач по высшей математике.1 курс.- М.: Айрис-пресс, 2003.

9. Лунгу К.Н., Письменный Д.Т. и др. Сборник задач по высшей математике.2 курс.- М.: Айрис-пресс,2007.

Типовые варианты контрольных работ Контрольная работа №1: «Матричная алгебра»

Задание 1. Найти _{и 2А + 3В,} если

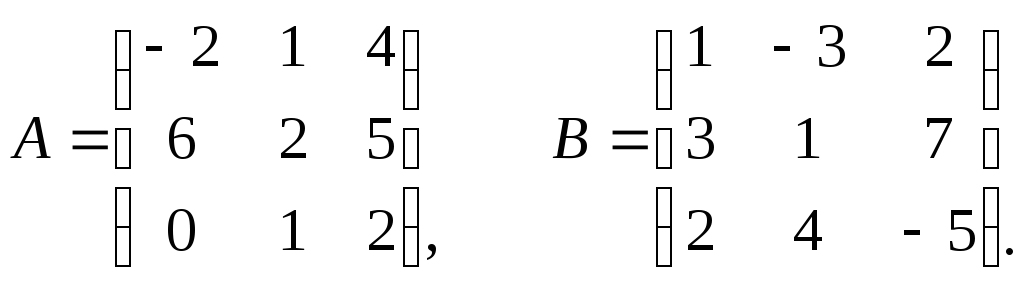
Задание 2.Вычислить определитель

Задание 3.Найти ранг матрицы

Контрольная работа №2: «Системы линейных уравнений»

Задание 1.Решить систему (если это возможно) методом Крамера и методом обратной матрицы

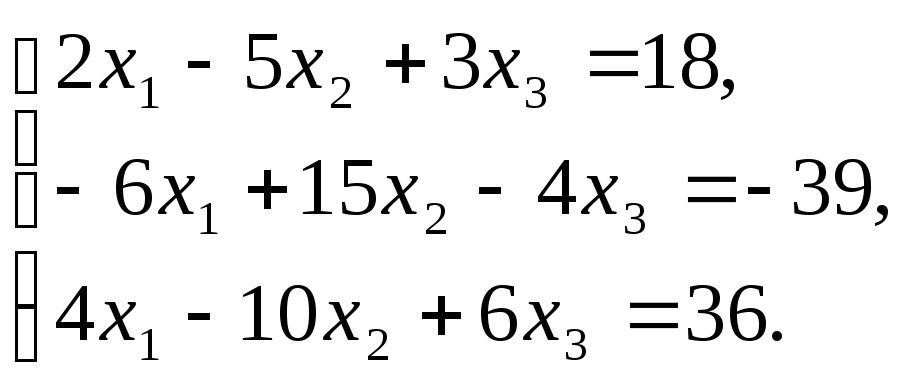
Задание 2. Решить систему методом Гаусса

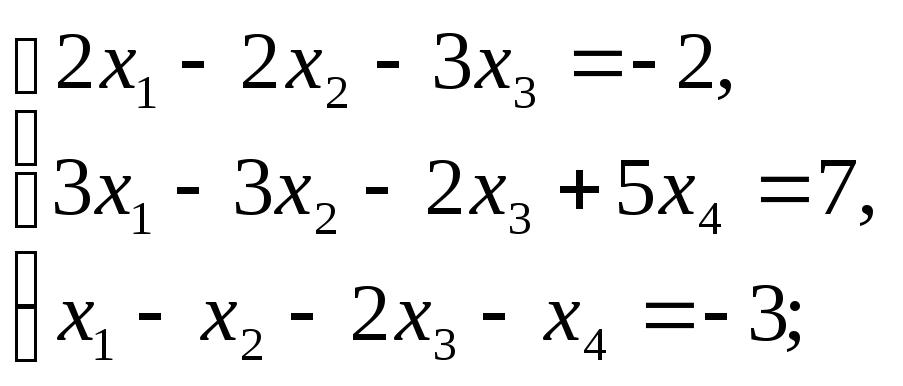
Задание 3. Найти фундаментальную систему решений системы уравнений:

Задания для индивидуальной работы

Задание 1. Дан параллелограмм ABCD, три вершины которого заданы. Найти: 1) четвертую вершину; 2) острый угол параллелограмма.

1. A(-1; -2; 3), B(-4; 1; 2), C (5; 2; 7).

2. A(1; 2; 3), B(3; -4; -2), C (-4; -3; 2).

Задание 2. Даны векторы ,,и .Показать, что векторы иможно взять в качестве базиса. Найти координаты вектора относительно выбранного базиса.

1. ,, .

2. ,, .

Задание 3. Найти собственные значения и собственные векторы линейного оператора, заданного матрицей

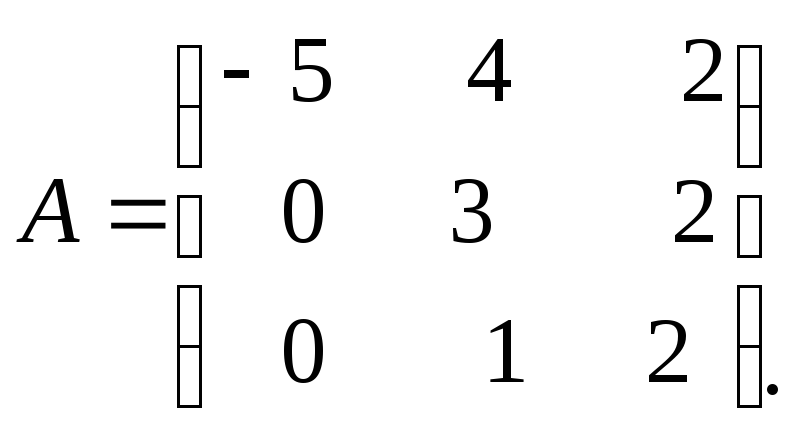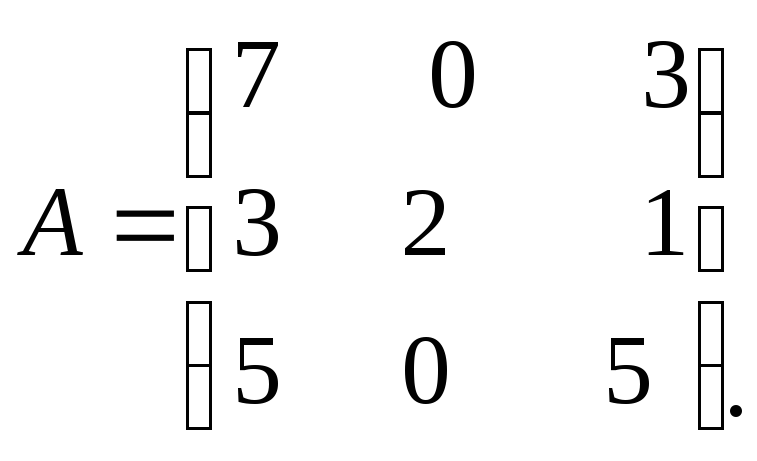1. 2.3.

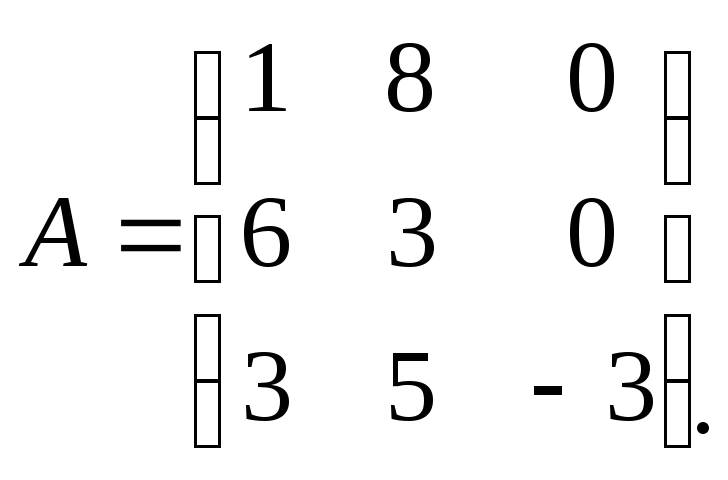
Задание 4. Привести к каноническому виду квадратичную форму

1. .

2. .

3. .

Задание 5. Исследовать на знакоопределенность квадратичную форму

1. .

2. .

3. .

4. Словарь терминов (глоссарий)

Матрицей размера , где- число строк,- число столбцов, называется прямоугольная таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится.Элементы матрицы обозначаются, где- номер строки, а-номер столбца

Если число столбцов матрицы равно числу строк , то матрица называетсяквадратной. Если , то матрица называетсясимметрической.

Квадратная матрица вида называется диагональной матрицей.

Квадратная матрица вида 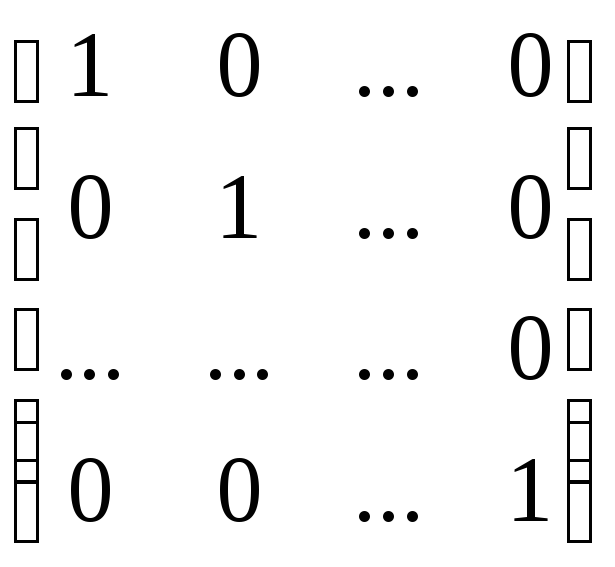называется единичной матрицей. Единичная матрица обозначается символом

Матрица, все элементы которой равны , называетсянулевой матрицей. Нулевая матрица обозначается символом

Суммой (разностью) матриц иназывается матрица,элементами которой являются соответственно сумма (разность) элементов исходных матриц

.

Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число

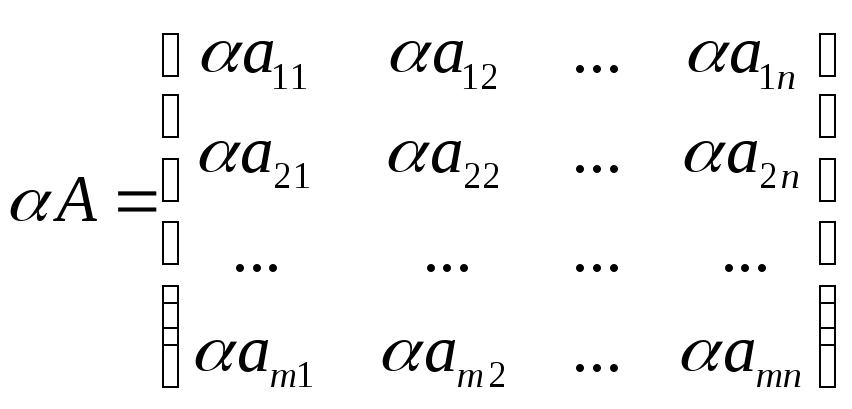
Произведением матрицы на матрицуназывается матрица, элементы которой могут быть вычислены по формуле

.

Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй. Умножение матриц, вообще говоря, не коммутативно, т.е. даже если определены оба произведения. Однако, если для каких - либо матриц равенствовыполняется, то такие матрицы называютсяперестановочными.

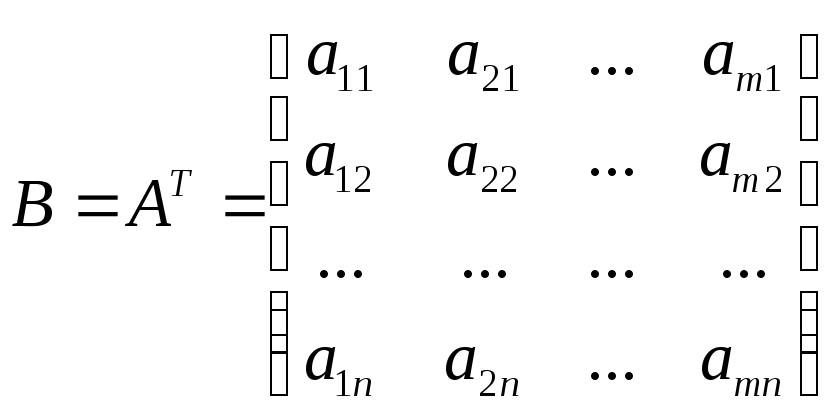
Матрицу называюттранспонированной матрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В другими словами, если . Матрица, транспонированная матрицеобозначается символом

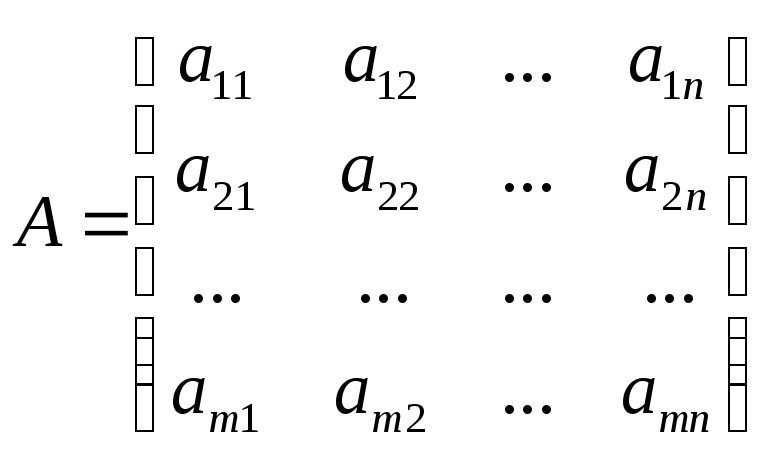
Определителем (детерминантом) квадратной матрицы называется число,которое может быть вычислено по элементам матрицы по формуле , где – детерминант матрицы, полученной из исходной вычеркиванием первой строки и– го столбца. Определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула

,

Определитель единичной матрицы равен 1. Для указанной матрицы А число называетсядополнительным минором элемента матрицы . Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.

Если в матрице А выделить несколько произвольных строк и столько же произвольных столбцов, то определитель, составленный из элементов, расположенных на пересечении этих строк и столбцов называется минором матрицы А. Если выделено строк и столбцов, то полученный минор называетсяминором порядка s.

Если вычеркнуть из исходной квадратной матрицы А выделенные строки и столбцы, то определитель полученной матрицы называется дополнительным минором.

Алгебраическим дополнением минора матрицы называется его дополнительный минор, умноженный на в степени, равной сумме номеров строк и номеров столбцов минора матрицы. В частном случае, алгебраическим дополнением элемента матрицы называется его минор, взятый со своим знаком, если сумма номеров столбца и строки, на которых стоит элемент, есть число четное и с противоположным знаком, если нечетное.

Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.

Элементарными преобразованиями матрицы называются следующие преобразования:

1) умножение строки на число, отличное от нуля;

2) прибавление к одной строке другой строки;

3) перестановка строк;

4) вычеркивание (удаление) одной из одинаковых строк (столбцов);

5) транспонирование.

Те же операции, применяемые для столбцов, также называются элементарными преобразованиями. С помощью элементарных преобразований можно к какой-либо строке или столбцу прибавить линейную комбинацию остальных строк (столбцов).

Если существуют квадратные матрицы Х и А одинакового порядка, удовлетворяющие условию где- единичная матрица того же порядка, то матрицаназываетсяобратной по отношению к матрице А и обозначается

Базисным минором матрицы порядка называется минор порядка, если он не равен нулю, а все миноры порядкаи выше равны нулю, или не существуют вовсе, т.е. числосовпадает с меньшим из чиселили.

Столбцы и строки матрицы, на которых стоит базисный минор, называются базисными. В матрице может быть несколько различных базисных миноров, имеющих одинаковый порядок.

Порядок базисного минора матрицы называется рангом матрицы. Элементарные преобразования не изменяют ранг матрицы.

Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.

Системой m линейных алгебраических уравнений относительно n неизвестных называется система

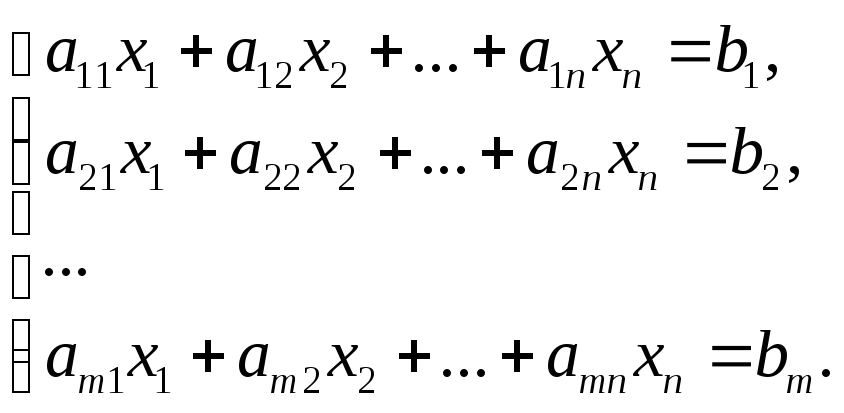
Решением системы m линейных алгебраических уравнений относительно n неизвестных называется совокупностьn значений неизвестных , при подстановке которых все уравнения системы обращаются в тождества.

Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения - несовместной.

Если правая часть системы m линейных алгебраических уравнений относительно n неизвестных равна нулю, то система называетсяоднородной.

Система из линейно независимых решений линейной однородной системы называетсяфундаментальной системой решений. Фундаментальная система решений образует базис в подпространстве решений линейной однородной системы.

Общим решением линейной системы называется выражение, позволяющее вычислить все решения системы.

Комплексным числом называется упорядоченная пара действительных чисели:, где(числоназывается мнимой единицей).

Комплексные числа называются сопряженными друг другу.

Пусть - множество элементов, для которых определены операции сложения и умножения на число, причём эти операции обладают следующими свойствами. Для любых элементов ,,из множества выполняются законы

1) (коммутативность сложения);

2) (ассоциативность сложения);

3) во множестве существует нулевой элемент такой, что для любого элемента,(существование нулевого элемента);

4) для любого элемента существует элемент, такой, что(существование противоположного элемента);

5) .

Для любых действительных чисел любых элементов,из множества ;

6) ;

7) Распределительный закон ;

8) .

Множество называется линейным (векторным) пространством, а его элементы называются векторами.

Если операции сложения и умножения на число определены для действительных элементов, то линейное (векторное) пространство является вещественным пространством, если для комплексных элементов – комплексным пространством.

Говорят, что в линейном пространстве задано некоторое линейное преобразование А, если любому элементу по некоторому правилу ставится в соответствие элемент.

Преобразование А называется линейным, если для любых векторов ии любоговыполняются равенства

Линейное преобразование называется тождественным, если оно преобразует каждый элемент линейного пространства в себя .

Если в пространстве существуют векторы линейного преобразования , то другой векторявляетсялинейной комбинацией векторов .

Если выполняется только при, то векторыназываютсялинейно независимыми.

Если в линейном пространстве есть n линейно независимых векторов, а любые векторов линейно зависимы, то пространство называется n-мерным, а совокупность линейно независимых векторов называется базисом линейного пространства .

Если вектор переводится в векторлинейным преобразованием с матрицейА, а вектор в векторлинейным преобразованием с матрицейВ, то последовательное применение этих преобразований равносильно линейному преобразованию, переводящему вектор в вектор(оно называетсяпроизведением составляющих преобразований).

Пусть – заданное n- мерное векторное пространство. Ненулевой вектор называетсясобственным вектором линейного преобразования А, если существует такое число , что выполняется равенство: . При этом число называетсясобственным значением (характеристическим числом) линейного преобразования А, соответствующего вектору .

Если линейное преобразование А в некотором базисе ,,…,имеет матрицу,то собственные значения линейного преобразования А можно найти как корни уравнения: .

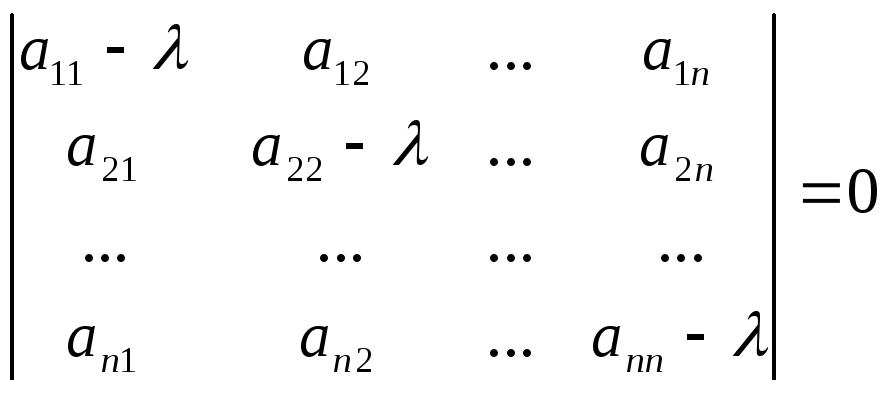Это уравнение называется характеристическим уравнением, а его левая часть - характеристическим многочленом линейного преобразования А. Характеристический многочлен линейного преобразования не зависит от выбора базиса.

Однородный многочлен второй степени относительно переменных и не содержащий свободного члена и неизвестных в первой степени называетсяквадратичной формой переменных и .

Однородный многочлен второй степени относительно переменных и

,

не содержащий свободного члена и неизвестных в первой степени называется квадратичной формой переменных и.

Квадратичная форма от n неизвестных называется положительно определенной, если ее ранг равен положительному индексу инерции и равен числу неизвестных.

Вектором (на прямой, на плоскости, в пространстве) называется упорядоченная пара точек А, В, или направленный отрезок. Точка А называется началом вектора, точка В - его концом. Вектор, начало и конец которого совпадают, называется нуль-вектором. Векторы обычно обозначаются или двумя большими буквами со стрелкой или чертой наверху, или малой буквой также со стрелкой или чертой наверху: ,,,. Первая из двух букв означает начало вектора, вторая - его конец.

Длина отрезка называетсядлиной или модулем вектора и обозначается или.

Два ненулевых вектора иназываютсяколлинеарными, если они лежат на одной или на параллельных прямых. Обозначение: .

Коллинеарные векторы называются одинаково (противоположно) направленными, если (в случае принадлежности разным прямым) их концы лежат по одну сторону (по разные стороны) от прямой, соединяющей их начала, а в случае принадлежности одной прямой, если из двух лучей, определяемых этими векторами, один содержится (не содержится) в другом. Обозначение ().

Два вектора иназываютсяравными, если они одинаково направлены и имеют равные длины, т.е. если ,=.

Отложить вектор от точкиМ -значит построить вектор , равный вектору.

Суммой векторов называется вектор , получающийся следующим построением: от произвольной точкиА (прямой, плоскости, пространства) откладываем первый вектор , равный вектору, от концавектораоткладываем второй вектор, равный векторуи т.д.: суммойявляется вектор,соединяющий начальную точку А с концом последнего отложенного вектора. Операция сложения векторов ассоциативна и коммутативна, так как при любом порядке откладывания векторов - слагаемых мы придем к тому же самому результату.

Произведением действительного ненулевого числа  на ненулевой вектор называется вектор, обозначаемыйили, удовлетворяющий следующим трем условиям:

Произведение любого вектора на нуль и нуль-вектора на любое число, по определению, есть нуль-вектор, т.е. =,=.

Скалярным произведением двух ненулевых векторов иназывается число, равное произведению длин этих векторов на косинус угла между ними. Обозначение: или, т.е.гдеЕслиили, то, по определению,

Декартова прямоугольная система координат в пространстве называется правой (левой), если поворот от базисного вектора к векторуна наименьший угол виден с конца вектораосуществляющимся против (по) часовой стрелки. Говорят также, что тройка базисных векторовимеет правую (левую) ориентацию.

Векторным произведением двух неколлинеарных векторов иназывается вектор, перпендикулярный плоскости векторови, имеющий длину, равную площади параллелограмма, построенного на векторахии направленный так, что тройка векторовтак же ориентирована, как и тройка базисных векторов. Обозначение:. Векторное произведение двух коллинеарных векторов и в случае, когда один или оба сомножителя - нуль-векторы, по определению, равно нулю.

Смешанным произведением трех векторов называется скалярное произведение векторного произведения первых двух векторов на третий. Обозначение:, т.е.Из этого определения следует, что три вектора компланарны (параллельны одной плоскости) тогда и только тогда, когда их смешанное произведение равно нулю.

Любая прямая на плоскости может быть задана уравнением первого порядка Это уравнение называютобщим уравнением прямой.

Каждый ненулевой вектор , компоненты которого удовлетворяют условиюназываетсянаправляющим вектором прямой .

Направляющими косинусами прямой называются направляющие косинусы вектора , которые могут быть вычислены по формулам:

; .

Откуда . Числа называютсяугловыми коэффициентами прямой.

14