
Metodicheskie
.Pdf
|
Содержание |
|
Введение ....................................................................................................................... |
4 |
|
1. |
Исследование положений равновесия нелинейной системы второго порядка 5 |
|
Задание 1 ...................................................................................................................... |
9 |
|
2. |
Производная в силу системы. Первые интегралы ............................................. |
10 |
Задание 2 .................................................................................................................... |
15 |
|
3. |
Дифференциальные уравнения с частными производными первого порядка 16 |
|
Задание 3 .................................................................................................................... |
21 |
|
4. |
Исследование устойчивости вторым методом Ляпунова ................................. |
24 |
Задание 4 .................................................................................................................... |
28 |
|
5. |
Исследование на устойчивость по первому приближению .............................. |
29 |
Задание 5 .................................................................................................................... |
35 |
|
6. |
Методы доказательства существования цикла .................................................. |
37 |
Задание 6 .................................................................................................................... |
42 |
|
7. |
Метод Пуанкаре в теории нелинейных колебаний............................................ |
44 |
Задание 7 .................................................................................................................... |
58 |
|
Библиографический список...................................................................................... |
59 |
|
Введение
Цель выполнения курсовой работы на тему «Элементы качественной теории дифференциальных уравнений и теории колебаний» – углубленное изучение теоретического материала и отработка практических навыков применения методов качественного исследования нелинейных дифференциальных уравнений и систем уравнений. Особое внимание уделяется вопросам исследования поведения решений уравнений и систем в окрестности особых точек, а также вопросам устойчивости и колебаний нелинейных систем.
Основное требование к курсовой работе – умение сочетать классические качественные методы исследования (прямой метод Ляпунова, теорию Пуанкаре-Бендиксона, метод Пуанкаре) с современными численноаналитическими методами исследования уравнений и систем, предполагающими использование стандартных программ, заложенных в математических пакетах Mathcad, Maple, Matlab, Matematica.
Исходные данные заданий курсовой работы содержатся в данных методических указаниях. Данные по каждому разделу курсовой работы предваряются формулировкой заданий, необходимым теоретическим материалом для их выполнения, а также рекомендациями и примерами выполнения аналогичных заданий.
Курсовая работа предусматривает выполнение семи заданий, тематика которых сформулирована непосредственно в тексте данных методических указаний. Объем курсовой работы не регламентируется и может варьироваться в зависимости от конкретного варианта задания.
Курсовая работа выполняется в течение 4-го семестра обучения, по мере изложения в лекционном курсе соответствующего теоретического материала и его отработки на семинарских занятиях. Защита курсовой работы проходит в форме индивидуальной беседы с преподавателем во второй половине мая текущего учебного года.
Пояснительная записка к курсовой работе должна содержать перечень заданий, выполненных в работе, с указанием математического пакета, использованного автором работы при их выполнении. В пояснительной записке также необходимо указать прикладные задачи, при решении которых могут быть использованы рассмотренные в работе методы исследования нелинейных систем.
4
1. Исследование положений равновесия нелинейной системы второго порядка
Рассмотрим нелинейную систему второго порядка:
dx |
|
f (x, y) |
|
||
|
|
||||
dt |
1 |
|
|
||
|
|
|
, |
(1.1) |
|
dy |
|
|
|
||
|
f |
|
(x, y) |
|
|
dt |
|
2 |
|
||
|
|
|
|
||
|
|
|
|
|
|
причем будем предполагать, что функции f1 (x, y), f2 (x, y) дважды непрерывно
дифференцируемы во всей плоскости XOY.
Положения равновесия (точки покоя) системы (1.1) определяются как решения системы уравнений:
f1(x, y) 0,f2 (x, y) 0.
Обозначим эти точки через Mi (xi , yi ), i 1, 2..., k .
Найдем матрицу Якоби J (x, y) (якобиан) системы (1.1):
f1 (x, y) |
f1 |
(x, y) |
||
|
x |
|
y |
|
J (x, y) |
|
|
||
f2 (x, y) |
f2 |
|
||
|
(x, y) |
|||
|
x |
|
y |
|
|
|
|
||
и вычислим значения Ai J (xi , yi ) для каждой из точек покоя Mi (xi , yi ), i 1, 2..., k . Пусть A (aij ) – одна из полученных матриц. Эта матрица задает линейную систему
|
dx |
|
a |
|
x a |
|
y |
|
|
|
|
|
|||||
|
dt |
11 |
12 |
|
|
|||
|
|
|
|
|
|
|
(1.2) |
|
|
dy |
|
|
|
|
|
||
|
a |
|
x a |
|
|
y |
||
|
|
21 |
22 |
|||||
|
dt |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Пусть 1, 2 – собственные значения матрицы A системы (1.2). Положение |
||||||||
равновесия Mi (xi , yi ) , для которого найдена рассматриваемая матрица, будем называть невырожденным, если 1 2 и Re 1,2 0. Оказывается, что в
невырожденном случае поведение траекторий вблизи положения равновесия Mi (xi , yi ) для нелинейной системы (1.1) в существенном совпадает с
поведением траекторий линейной системы (1.2) вблизи положения равновесия
(0,0).
За положением равновесия Mi (xi , yi ) системы (1.1) сохраним те же
названия, что и за положением равновесия системы (1.2): |
если 1 |
и |
2 |
|
вещественны и одного знака, то положение равновесия узел ( 1 0, 2 |
0 |
– |
||
устойчивый, 1 0, 2 0 |
– неустойчивый). Если 1 и |
2 комплексно- |
||
сопряженные с отрицательными (положительными) вещественными частями,
5
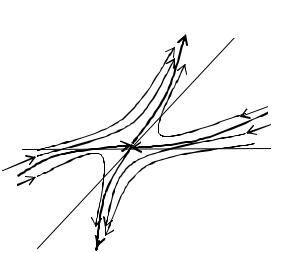
то положение равновесия Mi (xi , yi ) – устойчивый (неустойчивый) фокус. Если
1 и 2 вещественны и разных знаков, то положение равновесия – седло. Следующие теоремы, определяют поведение траекторий нелинейной
системы (1.1) |
вблизи невырожденного |
положения |
равновесия Mi (xi , yi ) в |
|
зависимости от типа точки покоя системы (1.2). |
|
|
||
Теорема 1.1. Предположим, что точка системы (1.2) является седлом. |
||||
Пусть Р – |
прямая, проходящая через точку |
Mi (xi , yi ) в направлении |
||
собственного |
вектора e1 матрицы |
A (aij ) , |
соответствующего |
|
отрицательному собственному значению 1 , а Q – прямая, проходящая через |
||||
точку Mi (xi , yi ) в направлении собственного вектора e2 |
матрицы A (aij ) , |
|||
соответствующего положительному собственному значению 2 , Тогда
существуют ровно две траектории U1 и U2 |
системы (1.1), которые при |
||||||||
t асимптотически |
приближаются к |
точке |
Mi (xi , yi ) . Эти две |
||||||
траектории |
вместе с точкой О |
|
|
Q |
|||||
образуют |
|
|
непрерывно |
|
|
||||
|
|
|
|
V1 |
|||||
дифференцируемую |
|
|
кривую, |
|
|
||||
|
|
|
|
|
|||||
касающуюся |
прямой |
Р |
в |
точке |
|
|
|
||
Mi (xi , yi ) . |
Точно |
|
|
также |
|
|
U1 |
||
существуют ровно две траектории |
|
|
|||||||
|
М |
||||||||
V1 |
и V2 , которые |
при |
|
t |
|
||||
асимптотически |
приближаются к |
|
|
P |
|||||
точке Mi (xi , yi ) , |
касаясь при этом |
U2 |
|
|
|||||
прямой Q. Остальные траектории в |
|
|
|||||||
|
|
|
|||||||
окрестности точки Mi (xi , yi ) ведут |
|
|
|
||||||
себя так, как показано на рис.1. 1. |
|
V2 |
|
||||||
|
Траектории |
U1 |
|
и |
U2 – |
|
Рис. 1.1 |
||
устойчивые усы седла, траектории |
|
|
|
||||||
V1 |
и V2 – неустойчивые усы седла. |
|
|
|
|||||
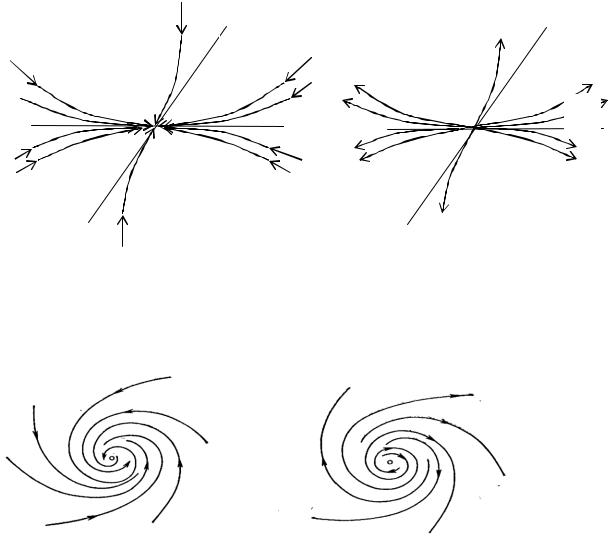
Теорема 1.2. Пусть точка Mi (xi , yi ) устойчивый (неустойчивый) узел, то есть1 2 0 (0 2 1) . В направлении собственного вектора, соответствующего 2 , проведем через точку Mi прямую Р, а в направлении собственного вектора, соответствующего 1 – прямую Q. Оказывается, что все траектории, начинающиеся достаточно близко от точки Mi , симптотически приближаются при t (t ) к точке Mi и имеют в
этой точке касательную. При этом только две траектории входят в точку Mi по касательной к прямой Q,, а остальные – по касательной к прямой Р
(соответственно при t и t ) (см. рис. 1.2).
6
|
|
|
Q |
0 |
|
|
Q |
2 |
0 |
2 |
|
||||
1 |
|
|
|
1 |
|
P
P
Рис. 1.2
Теорема 1.3.3. Пусть точка Mi – фокус, то есть 1,2 a bi, a 0, b 0 . Тогда при a 0 все траектории системы (1.1), проходящие вблизи точки Mi ,
при t наматываются на точку Mi , а при a 0 наматываются при t на точку Mi как спирали (см. рис. 1.3).
Устойчивый фокус |
Неустойчивый фокус |
Рис. 1.3
Пример 1.1. Найти особые точки системы:
dx |
|
4x2 y2 ; |
||
|
|
|||
(1.3) |
||||
dt |
||||
|
dy |
|
4x 2xy 8; |
|
|
|
|
||
dt |
|
|
||
определить их тип. Построить схематически фазовый портрет в окрестности каждой особой точки.
Решение. Для нахождения особых точек решим систему уравнений
4x2 y2 0
4x 2xy 8 0 x1 2, y1 4; x2 1, y2 2.
Итак, особыми будут точки M1(2, 4) и M2(–1,–2).
Найдем матрицу Якоби системы: |
|
8x |
2 y |
|
J (x, y) |
2 y 4 |
2x |
. |
|
|
|
|
||
7
Для точки M1(2, 4) |
имеем |
16 |
8 |
|
A1 . |
Для точки M1(-1,-2) |
|||||
J (2,4) |
4 |
4 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
8 |
4 |
|
A2 . |
|
|
|
|
|
|
|
|
имеем J ( 1, 2) |
2 |
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
Собственные |
значения |
матрицы |
A |
16 |
8 |
|
1 12, 2 8 – |
||||
1 |
4 |
|
4 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
e2 (1, 1) |
положительны, |
поэтому |
||||
особая |
точка |
M1(2, |
4) |
|||
|
является |
|
точкой |
типа |
||
e1 (2, 1) |
"неустойчивый узел". |
|
||||
|
Для |
|
построения |
|||
|
фазового |
|
портрета |
в |
||
(2,4) |
окрестности |
точки |
M1(2, 4) |
|||
найдем собственные векторы, |
||||||
|
||||||
|
соответствующие найденным |
|||||
|
собственным |
|
значениям |
|||
|
матрицы |
|
А1. |
Имеем: |
||
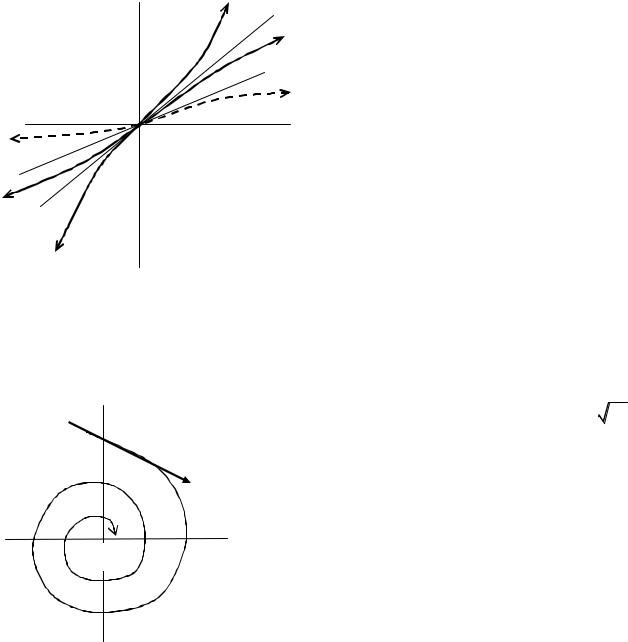
Рис.1.4 |
e1 (2, 1), e2 (1, 1) . |
Согласно |
||||
теореме |
1.2, только |
две |
||||
|
||||||
траектории выходят из особой точки M1(2, 4) по касательной к направлению, определяемому собственным вектором e1 , а остальные выходят из нее по
касательной к направлению, определяемому вектором e2 |
(рис.1.4) |
|
||||||
Собственные |
значения |
матрицы |
A2 |
8 |
4 |
|
– |
комплексно- |
|
|
|
||||||
|
|
|
|
8 |
2 |
|
|
|
|
|
|
|
1,2 |
|
|
|
|||
e (0,0796; 0,04) |
сопряженные |
числа |
5 i 23 . |
|||||||
Поэтому состояние равновесия M2(–1,–2) |
||||||||||
|
|
|||||||||
|
|
– устойчивый фокус. Все траектории, |
||||||||
|
|
начинающиеся |
в достаточно |
малой |
||||||
|
|
окрестности точки M2, спиралевидно |
||||||||
|
|
наматываются на эту точку. |
|
|
|
|
||||
(-1,-2) |
|
Для |
определения |
|
направления |
|||||
|
закручивания |
спиралей |
достаточно |
|||||||
|
|
|||||||||
|
|
выбрать какую-либо точку в достаточно |
||||||||
|
|
малой окрестности точки М2 и |
найти |
|||||||
|
|
вектор, |
касательный |
к |
траектории |
|||||
Рис. 1.5 |
|
системы |
в выбранной |
точке. |
Так, |
|||||
|
|
например, для точки М(–1; –1,98) вектор |
||||||||
касательной будет таким: |
e (0,0796; 0,04) . Это означает, что спирали будут |
|||||||||
закручиваться по ходу часовой стрелки (рис.1.5).
8

Замечание 1.1. Для того, чтобы найти особые точки уравнения
dy 4x 2xy 8 , следует перейти к эквивалентной системе (1.3) и рассуждать dx 4x2 y2
так же, как и в примере 1.1.
Задание 1
Найти особые точки следующих систем. Определить их тип. Построить схематически фазовый портрет в окрестности каждой особой точки.
x 1 y x( y 1); 1. y xy 4.
x y x 1;
2.
y ln(x2 y).
x 2x( y 1);
3.
y x2 y3 8.
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4x |
2 |
|
|
|
2 |
|
|
|
|
|
4. |
|
y |
; |
|
|
|
|||||
|
y 2x( y 2) 8. |
||||||||||
|
x 2xy; |
|
|
|
|
|
|
|
|||
5. |
|
|
|
|
|
|
|
|
|
|
|
|
y 4 y2 x2 4. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x x |
2 |
y |
2 |
12; |
||||||
6. |
|
|
y2 20. |
||||||||
|
y x2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
; |
|
|
|
|
|||
|
x y |
2 |
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
||
7. |
|
|
1 x x |
2 |
|
|
|||||
|
|
|
|
|
|||||||
|
y ln |
|
. |
|
|||||||
|
|
|
|
||||||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 3y sin x; |
||||||
|
x 2 y |
|
|||||||||
8. |
|
|
|
|
|
|
|
|
|
|
|
|
y sin x. |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
; |
|
|
|
|
||
|
x e |
y |
|
|
|
|
|
||||
|
|
|
x |
|
|
|
|
|
|
||
9. |
|
|
|
|
|
|
|
|
|
|
|
|
y ln(5 x2 ). |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
x ( y 1)(3x y 5);
10.
y x2 y2 5.
x x(x2 2) y; 11.
y x(3x4 1) 2 y.
x ln(1 y y2 ) ln 3; 12.
y arctg(x2 y2 ).
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
13. |
x ln(1 3x x ); |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y x2 |
3y2 12. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
9; |
|
|
x 10x |
2 |
2 |
|||||||
|
|
|
|
|
|
|
|
|||
14. |
|
|
2 |
|
1. |
|
|
|||
|
y e4 x x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
y2 |
|
|
|
|||
15. |
x 1 e |
|
|
|
|
|
; |
|
|
|
|
y ln(1 y2 ) ln 2. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
x x2 y2 5;
y (x 1)(x 3y 5).
x x y 2xy y2 ;
y x 2x2 xy.
x arctg(x y y2 );
y y2 4x.
x sin y;
y sin x sin y.
|
|
|
|
|
|
|
|
|
|
|
|
(x y) |
2 |
3 2; |
|||||
|
x |
|
|||||||
20. |
|
|
|
|
|
|
|
|
|
|
y ey2 x e. |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
21. |
x |
x |
|
y |
2 2; |
||||
|
y arctg(x2 |
|
xy). |
||||||
|
|
|
|
|
|
|
|
|
|
x x y 2x3;
y x y.
x x xy;
y y y2 xy x3.
9

|
|
|
|
|
|
|
2 y |
|||
|
x 1 x |
|
|
|
|
x; |
||||
|
1 |
|
|
|||||||
24. |
|
|
|
|
|
x |
||||
|
|
|
|
y |
|
|
||||
|
|
|
|
|
||||||
|
y |
2 |
|
|
|
|
|
y. |
||
|
|
|
|
|
||||||
|
|
|
|
|
1 x |
|||||
|
|
|
|
|||||||
|
|
|
|
; |
|
|
|
x y x |
|
|
|||
|
|
3 |
|
|
|
|
25. |
|
|
|
|
|
|
|
y x y3. |
|
|
|||
|
|
|
|
|
|
|
|
x y; |
|
|
|
|
|
26. |
|
|
|
|
|
|
|
|
x |
5 |
|
||
|
|
|
|
|||
|
y x |
|
y. |
|||
|
|
|
||||
|
|
16 |
|
|||
x 2x xy;
y 2x2 y.
x y;
y x 2arctg(x y).
x x y xy y2 ;
y 2x x2 xy.
x x y 0,5xy y2 ;
y 0,5x 0,5x2 xy.
x (2x y)2 9;
y (x 2 y)2 9.
2. Производная в силу системы. Первые интегралы |
|
|||
Рассмотрим систему: |
|
|
|
|
x f (x), |
x Rn , f (x) col( f |
(x)),i 1, |
,n. |
(2.1) |
|
i |
|
|
|
Определение 2.1. Функция u(x) называется первым интегралом |
||||
автономной системы (2.1), если она постоянна вдоль |
каждой |
фазовой |
||
траектории этой системы, то есть если u[ (t)] const |
для любого решения |
|||
x (t) системы (2.1).
Теорема. Для того, чтобы функция u(x) была первым интегралом системы (2.1), необходимо и достаточно, чтобы ее производная в силу этой системы тождественно обращалась в нуль, то есть чтобы выполнялось соотношение:
n |
u |
|
|
|
u(x) |
fi (x) (grad u, f (x)) 0. |
(2.2) |
||
x |
||||
i 1 |
|
|
||
i |
|
|
Первый интеграл u(x) системы, это некоторый закон сохранения энергии в этой системе. При движении вдоль траекторий системы величина u(x) сохраняет свое первоначальное значение. Именно из этих соображений и были получены первые интегралы многих уравнений классической механики.
Пример 2.1. Одномерное движение материальной частицы массы m в потенциальном поле описывается уравнением Ньютона:
|
(2.3) |
mx U (x). |
Здесь U(x) – потенциал поля. Первый интеграл уравнения (2.3) – функция v(x, x) , которая постоянна при x (t), x (t) , где x (t) – решение этого
уравнения.
Для того, чтобы найти первый интеграл, умножим обе части уравнения
(2.3) на x :
10
|
|
|
|
|
|
d mx2 |
|
|
|||
|
mxx U (x)x |
|
|
|
|
U (x) |
0. |
||||
|
|
|
|
||||||||
|
|
|
|
|
|
dt 2 |
|
|
|||
Таким образом, v(x, x) |
mx2 |
U (x) |
и есть |
первый |
интеграл уравнения |
||||||
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
|||
(2.3). Этот интеграл носит название интеграл энергии, |
поскольку он равен |
||||||||||
|
mx2 |
|
|
|
|
|
|
||||
сумме кинетической |
|
и потенциальной U(x) энергии частицы. Как видим, |
|||||||||
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
в данном случае сумма кинетической и потенциальной энергии механической системы постоянна:
|
|
mx2 |
U (x) E const , |
(2.4) |
||
|
|
|
||||
|
|
|
2 |
|
|
|
то есть |
рассеяние |
энергии |
отсутствует. Такие |
системы называют |
||
консервативными. Если |
заданы |
начальные условия |
x(0) x0 , x(0) x0 , то |
|||
E |
mx |
2 |
U (x ) . |
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
||
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Отметим, что уравнение (2.3) эквивалентно системе |
|
||||
|
|
|
x y, |
|
|
|
|
|
|
|
|
|
(2.5) |
|
|
|
|
|
||
|
|
|
U (x) |
|
|
|
|
|
|
y |
|
. |
|
|
|
|
|
|
||
|
|
|
|
m |
|
|
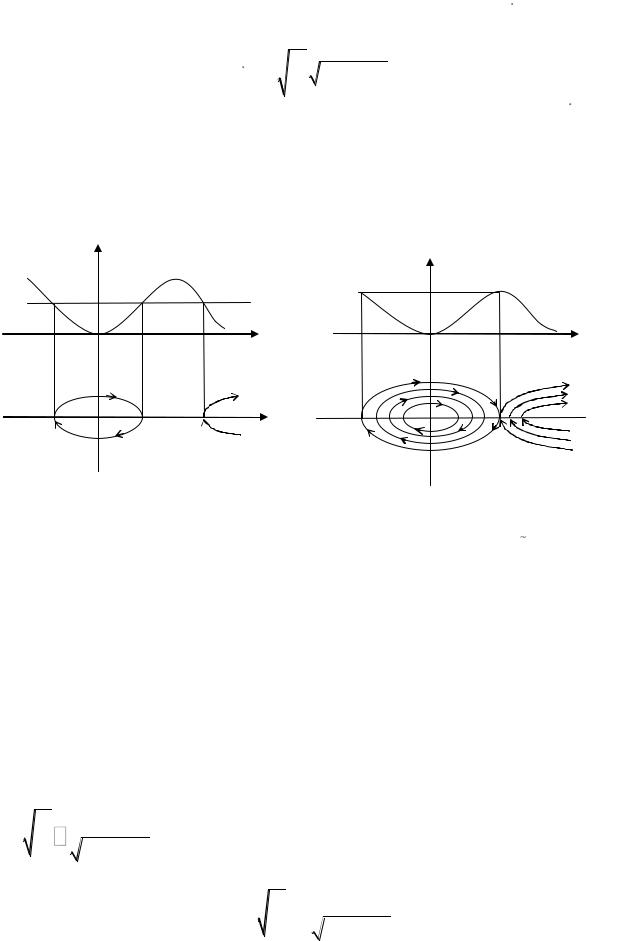
Точки покоя системы (2.5) определены соотношениями y 0,U (x) 0 , то есть имеют координаты (xi ,0) , где xi – абсциссы точек экстремума функции U (x) .
Соотношение (2.4) позволяет исследовать и построить фазовый портрет уравнения (2.3) на плоскости (x, x) (системы (2.5) на плоскости (x, y) ),
рассматривая ее фазовые траектории как однопараметрическое семейство
кривых, где роль параметра играет величина E полной энергии системы. |
|
|||||||||||
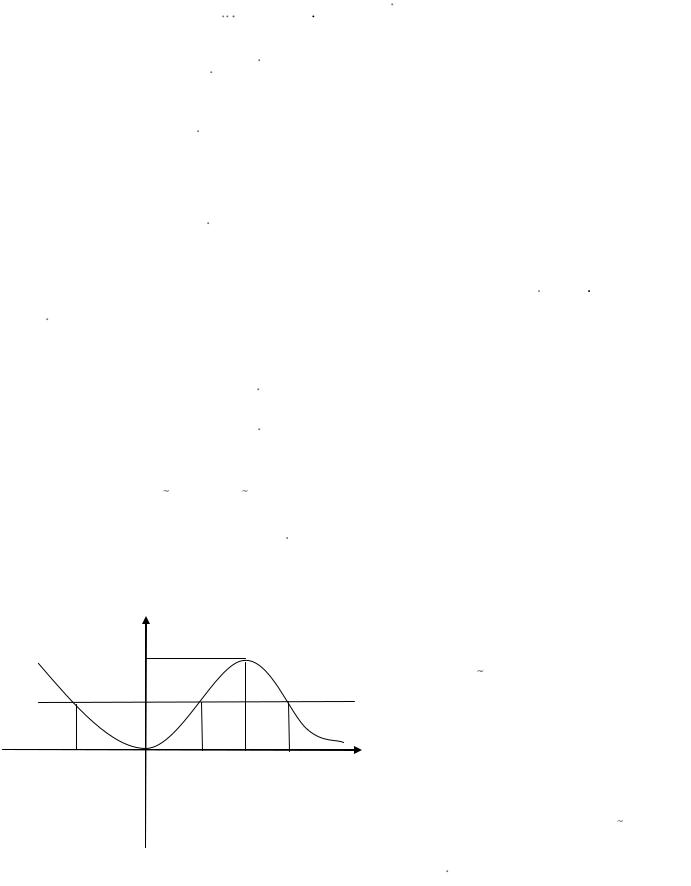
|
|
|
|
|
|
|
Пусть, например, график |
|||||
U(x) |
|
|
|
|
функции |
U(x), |
|
имеет |
вид, |
|||
Е0 |
|
|
|
показанный на рис. 2.1. Точки |
||||||||
|
|
|
|
|||||||||
|
E |
|
|
|
О |
|
и |
x |
соответствуют |
|||
|
|
|
|
состояниям |
|
равновесия |
||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
системы |
(точкам |
экстремума |
|||||
|
|
|
~ |
|
функции U(x) потенциальной |
|||||||
x1 |
O |
x2 |
x3 |
энергии системы). |
|
|
||||||
|
x |
|
|
|||||||||
|
|
|
|
|
|
Построим |
|
фазовый |
||||
|
|
|
|
|
портрет |
|
|
|
системы. |
|||
|
|
Рис.2.1 |
|
|
Положим E0 maxU (x) =U (x) . |
|||||||
|
|
|
|
Зададимся |
|
некоторым |
||||||
|
|
|
|
|
|
|||||||
значением |
E E . Из (2.4) |
следует, что U[x(t)] E |
mx2 (t) |
E |
вдоль любого |
|||||||
|
||||||||||||
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
решения системы |
(2.5). |
Значит траектории |
этих решений |
таковы, |
что |
|||||||
11
x(t) (x1, x2 ) или |
x(t) (x3 , ) . При этом связь между x и |
y x определяется |
||||||
соотношением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
x |
|
|
E U (x) . |
(2.6) |
|||
|
|
|
|
|||||
|
m |
|||||||
Направление движения вдоль траекторий определяется так: при x 0 (то есть в верхней полуплоскости) x(t) возрастает как функция времени. Соответственно, в нижней полуплоскости она убывает. Для значения E, выбранного так, как указано на рис.2.2, получим две траектории системы (см. рис.2.2). Варьируя значения E, можем схематически построить фазовый портрет системы (2.5) (рис.2..3).
U(x) |
|
|
U(x) |
|
E |
|
|
|
|
|
|
|
|
|
x1 O |
x2 |
X |
O |
~ |
|
x |
|||
|
x |
|
|
|
|
|
|
x |
|
|
Рис. 2.2 |
|
Рис. 2.3 |
|
Отметим, что структура траекторий в окрестности точки (x,0) такая же,
как и в окрестности седла. Кривые «входящие» в указанную особую точку и «выходящие» из нее – сепаратрисы седла. Сепаратрисы разделяют области на фазовой плоскости с различным типом поведения траекторий.
Структура траекторий в окрестности точки (О,О) такая же, как в окрестность центра. Все траектории в указанной окрестности являются замкнутыми траекториями (циклами), что соответствует периодическим
движениям системы. |
Периодическое движение происходит в области |
|
xmin x1 |
x x2 xmax , в |
которой U (x) E , причем равенство достигается на |
концах |
интервала, т.е. |
xmin и xmax представляют собой корни уравнения |
U (x) E . В этом случае мы можем проинтегрировать выражение (2.6) по всей
замкнутой |
фазовой |
кривой |
|
|
и |
определить |
период |
колебания |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
T |
m |
dx |
|
. |
Используя |
|
|
правило вычисления криволинейного |
||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
2 |
|
|
||||||||||||||||||
E U (x) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
интеграла, этому интегралу можно придать вид |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
xmax |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
m |
dx |
|
|
||||||
|
|
|
|
|
|
|
|
|
T 2 |
|
|
x |
|
|
|
. |
|
(2.7) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
E U (x) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
min |
|
|
|
|
|
||
12
