Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тульский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Metodicheskie

.Pdf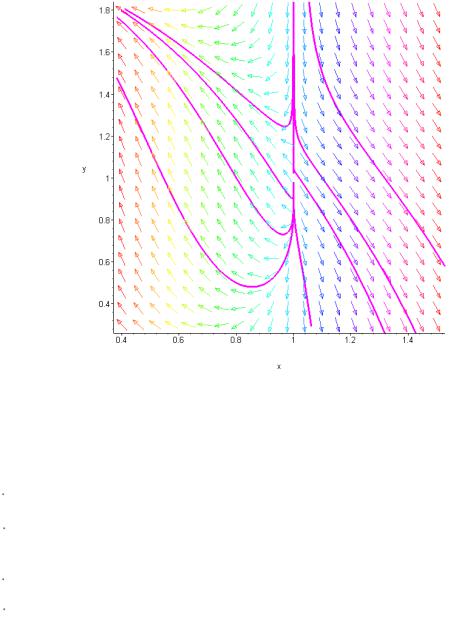

Скачиваний:

Добавлен:

10.05.2015

Размер:

1.79 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Рис. 5.3. Фазовый портрет системы в окрестности точки M 3 (1;1)

Пример 5.3.

С помощью теоремы об устойчивости по первому приближению найти значения параметров a и b, при которых асимптотически устойчиво нулевое решение системы

x x ay 4sin y2 ;

y tg bx 2 a y.

Решение. Система первого приближения в данном случае имеет вид:

	x x ay;
			a y.
	y bx 2
Составим соответствующее ей характеристическое уравнение:
	1	a		0 2 a 3 2 ab a 0.

	b 2 a

Оба		корня	полученного уравнения будут иметь отрицательные

a 3;

вещественные части, если выполняются условия . Область

2 ab a 0.

асимптотической устойчивости рассматриваемой системы на плоскости (a,b) изображена на расположенном ниже рисунке.

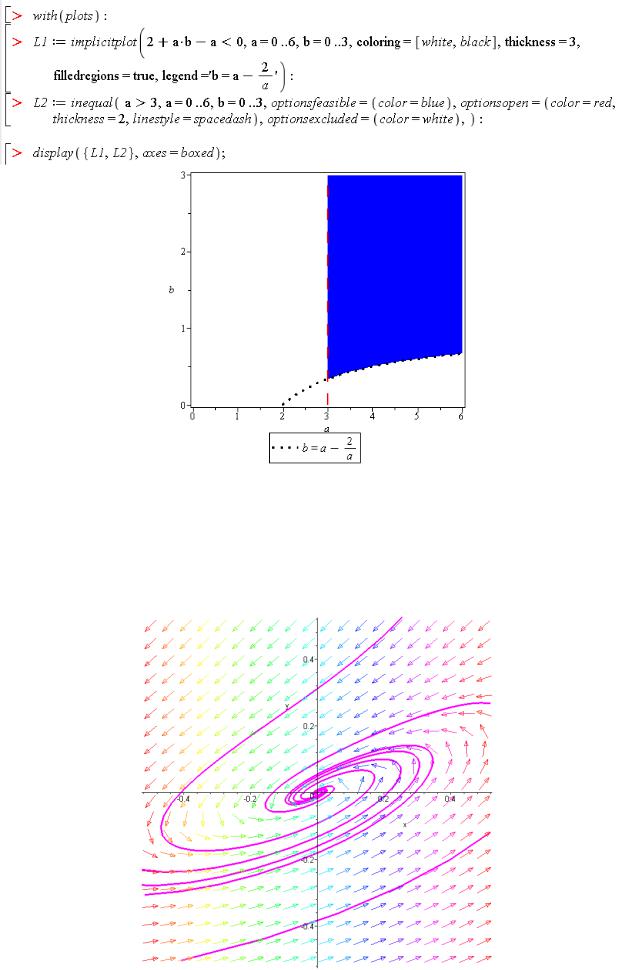
Рис. 5.4. Область асимптотической устойчивости в пространстве параметров

Результаты численного интегрирования рассматриваемой системы показывают, что при a 4 , b 1 точка покоя 0;0 является устойчивой (устойчивый фокус), а при a 5 , b 0,2 - неустойчивой (точка покоя типа «седло»).

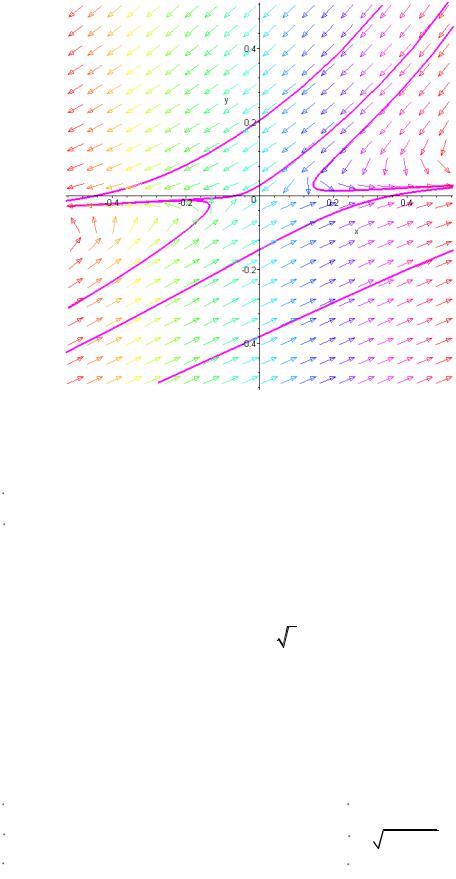
Рис. 5.5. Фазовый портрет системы при a 4 , b 1

Рис. 5.6. Фазовый портрет системы при a 5 , b 0,2

Пример 5.4.

Исследовать на устойчивость решение x 0, y 0 системы

x 3x y x2 ,

y x 2 y x2 sin t.

Решение. Матрица системы первого приближения имеет вид:

						3	1
	J (0,0)						.
						1	2
Ее собственные значения		5	i		3		. Поэтому нулевое решение
Ее собственные значения			i				. Поэтому нулевое решение
1,2	2			2
	2			2

рассматриваемой системы неустойчиво по Ляпунову.

Задание 5

С помощью теоремы об устойчивости по первому приближению исследовать на устойчивость нулевое решение системы:

x 3x sin y z;

1.y e2 x 1 2 y 3z;z x 2 y 5tg z.

x tg(z y) 2x;

2.y 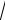9 12x 3ey ;z 3y.

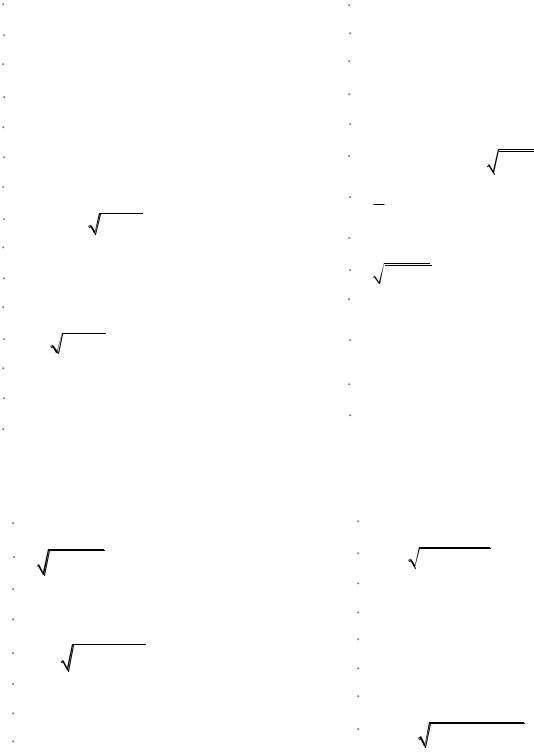
x 10x 4ey 4cos y2 ; 3.

y 2ex 2 y x4.

x 2.5xe

;

3y sin x

ye 0.5 y

y4 cos x.

y 2x

1) 9 y x ;

x 0,25(e

y 0,2x sin y y14.

);

x ln(4 y e

1 3 1

6x.

y 2 y

x x 1 cos y;

y sin

2 x 1 ey .

x 2 y

cos 2x;

x x

1 2x

2ey 3y.

y 1

x y 2x sin z;

4 yey 5z;

y x

z e

x ex e 3z ;

10. y 4z 3sin(x y);z ln(1 z 3x).

x 7x 2sin y y4 ; 11.

y ex 3y 1 2,5x.

x 0,75sin x 7 y 3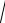1 y x5;

12. y 2 x 3y cos y 11y5.

x ex 2 y cos3x; 13.

y 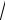4 8x 2ey .

x tg( y x);
14.	y
y 2		2cos	x .
		3

x 2ex 5y 2 x4 ; 15.

y x 6cos y 6 y2.

С помощью теоремы об устойчивости по первому приближению исследовать на устойчивость все состояния равновесия системы

x e y ex ;

y 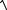3x y2 2.x y x2 x;

y 3x x2 y.


		2
18. x 3	4 x		y;
y ln(x2	3).

x (x 1)( y 1);

y xy 2.

x ln(1 y sin x); 20.

y 2 33sin x 8.

x ln( x y2 );

21.

y x y 1.

x y;

22.

y sin(x y).

x sin y; 23.

y 2x 1 3x sin y.

С помощью теоремы об устойчивости по первому приближению найти значения параметров a и b, при которых асимптотически устойчиво нулевое решение системы:

x ax 2 y x2 ;

y x y xy.

x x ay y2 ;

y bx 3y x2.

		x
				4 ay;
26.	x 2e

	y ln(1		x ay).

		2	ay;
27.
	x 3y
	y 2x (2 a) y.

x ax y x2 ; 28.

y x ay y2.

x y sin x;

29.

y ax by.

x ln(e ax) ey ;

30.

y bx tg y.

x ax y (a 1)x2 ;

31.

y x ay.

6. Методы доказательства существования цикла

Рассмотрим систему
x f (x), x R2 .	(6.1)
Будем считать, что для этой системы везде в	R2 выполнены условия

теоремы существования и единственности решения и имеет место непрерывная зависимость решений от начальных данных. Все эти условия, например, выполнены, если правая часть системы есть дифференцируемая функция везде в R2 .

	Принцип кольца
		Пусть	на	плоскости		имеется
		замкнутая	кольцеобразная			область,
		ограниченная		двумя	замкнутыми
		гладкими кривыми 1 и 2			( 1	и 2 не
		являются траекториями системы (6.1)) ,
		такая, что все траектории системы (6.1)
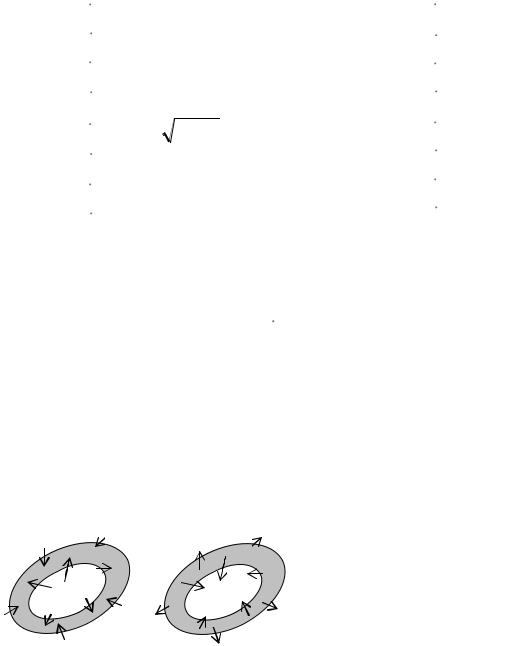
Положительно	Отрицательно	входят вовнутрь этой области с ростом
Положительно	Отрицательно	t и в дальнейшем не покидают ее (или
инвариантная	инвариантная	t и в дальнейшем не покидают ее (или
инвариантная	инвариантная
область	область	входят в эту область при убывании t и

	не покидают ее	при	t ).	Такая
Рис. 6.1	область называется		положительно
	(отрицательно)	инвариантной		для

траекторий системы (рис. 6.1).

Лемма 6.1. Если внутри положительно (отрицательно) инвариантной для траекторий системы (6.1) области нет состояний равновесия системы, то в этой области содержится по крайней мере один цикл системы (6.1).

Существование циклов у систем с единственным положением равновесия

Теорема 6.1. Если все собственные значения матрицы Якоби J (x)

системы (6.1) при x 0 имеют положительные вещественные части и система диссипативна, то она имеет по крайней мере один цикл.

		Критерии диссипативности
Теорема	6.2.	Система		x Ax (x,t)		с	гурвицевой	матрицей А		и
ограниченной функцией (t, x)				диссипативна по Левинсону.

Теорема	6.3.	Пусть	( )d		ограничен		при всех	и	матрица	A
			0
гурвицева. Тогда		система		x Ax b ( )		( ( ) – скалярная функция
переменной cT x , b и с – n-векторы.) диссипативна.
Теорема	6.3. Пусть			на	множестве		{x :\| x \| R1}		определена

неотрицательная дифференцируемая функция v(x) , обладающая следующими свойствами:

1) lim v(x) ,

|x|

2)v(x) (grad v(x) f (x)) 0 при | x | R1 ,

3)среди решений x(t) системы (2.7.8) не существует таких, для которых

v[x(t)] 0 при | x | R1 .

Тогда система (6.1) диссипативна.

Проиллюстрируем на примерах применение леммы 6.1 и теоремы 6.1 для доказательства существования циклов.

Пример 1. Доказать, что система

x 5x y x(x

);

x 5y y(x2 y2 );

(6.2)

имеет цикл.

0;0

Покажем, что система (6.2) имеет единственное состояние равновесия

5x y x(x2 y2 ) 0,

5x y

x 5y y(x2 y2 ) 0.

x 5y y(x y ) 0.

5x y

x 0,

5xy y2

x 5 y

Рассмотрим функцию v(x, y) x2 y2 . Ее производная в силу системы

(6.2)	имеет	вид v 2 x2 y2 (x2 y2			5) . Рассмотрим две концентрические
окружности		x2 y2	2 и	x2 y2 7 .	На первой из них выполнено условие
v 0 ,	а на	второй	v 0.	Поэтому траектории системы пересекают первую

окружность по направлению «к центру», а вторую – по направлению «от центра».

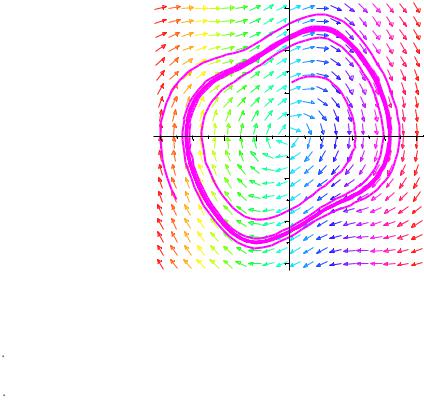
Значит, в фазовом пространстве рассматриваемой системы имеется отрицательно инвариантное кольцо (рис. 6.1), в котором нет точек покоя системы. Согласно лемме 6.1, такая система имеет цикл.

На приведенном ниже рис. 6.1. изображен цикл системы (6.2), найденный путем численного интегрирования, а также траектории, навивающиеся на этот цикл при t изнутри и снаружи.

Рис. 6.2. Численное интегрирование системы (6.2)

Пример 2. Доказать, что уравнение x x4 3 x 2x 0 имеет цикл. x4 4

Решение:

Запишем данное уравнение в виде эквивалентной системы в R2 , сделав замену x x1, x x2 :

x		x ,
	1		2			(6.3)
			3 x4		x2 2x1.	(6.3)
x2				1
x2			4	4
			x1	4

Покажем, что система (6.3) имеет единственное неустойчивое состояние равновесия 0;0 :

x		0,																	x2 0,
2																			x2 0,
3 x				4	x2 2x1 0.																	0.
		1																	x1
	4																		x1
x1		4
			Составим якобиан системы и найдем его значение в точке 0;0 .
		x1 x2 ,																							x x ,
									x4				4					7								1	2
									x4				4					7									2x1 x2					7x
				x							1									x			2x .			x2								2	.
																																4
												4																				4
				2							x	4			4				2				1									x1	4
											x				4																	x1	4
											1
																			0								1
				J x , x																28x13 x2							7
				J x , x											2					28x13 x2				1			7
							1			2
							1			2									x4			4 2
																			x4			4 2					x14 4
																			1
											0							1
			J 0,0															3
											2							3
											2
																		4
			Составим характеристическое уравнение системы:
										1									3
										1
								3					2								2 0
			2
																			4
							4												4
							4
			Оба корня характеристического уравнения имеют положительные
вещественные части.
			Значит, система (6.3) имеет единственное неустойчивое состояние
равновесия										0;0 .
			Докажем, что система диссипативна.																																	x Ax b , где
			Очевидно, что систему можно записать в																													виде				x Ax b , где
cT x .
							0					1								0			, x1		,				1
			A				2										,	b													.
			A														,	b											4	4	.
											1									7										4
			Характеристический																				полином				линейной					части					системы				2 2
гурвицев.
																																		dt
			Докажем ограниченность интеграла																											t dt				dt			.
			Докажем ограниченность интеграла																											t dt				4			.
																												0				0	t			4
																												0				0
						dt									dt
						dt									dt

				t4		4						t4 4
		0									0
																	dt																					t	4
			Интеграл														dt			сходится, так как выполнено условие lim																		t			1 0 .
			Интеграл														4			сходится, так как выполнено условие lim																		4			1 0 .
														0		t		4																			t t			4
														0

Значит, система (6.3) диссипативна согласно теореме 6.3.

Таким образом, по теореме 6.1 система (6.4)по крайней мере один цикл.

На рис. 6.3 представлены результаты численного интегрирования системы

(6.3).

				6
				4
			y
				2
4	3	2	1	0	1	2	3	4
						x
				2
				4
				6

Рис. 6.3. Численное интегрирование системы (6.3)

Пример 3. Доказать, что система

	20x
x 2x 3y
x 2x 3y	x2 8
	x2 8	(6.4)

y x

имеет цикл.

Решение:

Покажем, что система (6.4) имеет единственное неустойчивое состояние

равновесия 0;0 :
x 0,												x 0,
												x 0,
					20x
2x 3y										0.		y 0.
2x 3y					x	2				0.		y 0.
					x		8
		Составим якобиан системы и найдем его значение в точке 0;0 .
													8 x	2
														2
									2 20							3
			J x, y						2 20				x2 8		2	3
			J x, y										x2 8

												1				0
							1
	J			0,0						3
							2			3
							2

						1				0
		Составим характеристическое уравнение системы:
					3						1
		1
	2							2				3 0

			1								2
											2

Оба корня характеристического уравнения имеют положительные вещественные части.

Значит, система имеет единственное неустойчивое состояние равновесия
0;0 .
Докажем, что система диссипативна.
Система имеет вид	x Ax x . Матрица A для рассматриваемой
2	3		2 2 3
системы имеет вид A		. Ее характеристический полином	2 2 3
1	0

20x

гурвицев, а функция x2 8 ограничена.

Значит, система диссипативна согласно теореме 6.2.

Таким образом, все собственные значения матрицы Якоби J (x, y) системы в точке 0;0 имеют положительные вещественные части и система

диссипативна, следовательно, она имеет по крайней мере один цикл.

На рис. 6.4 представлены результаты численного интегрирования системы (6.4).

Рис. 6.4. Численное интегрирование системы (6.4)

Задание 6

Используя теорему Пуанкаре-Бендиксона, доказать существование цикла у уравнения или системы

1. x [2 e 2 x2 (x 3)]x 5x 0.

<<< < Предыдущая 1 2 34 / 64 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
26.09.2019156.16 Кб1Materialy_k_IGA (1).doc
#
10.05.20151.93 Mб35MathCadTV 5semestr.pdf
#
10.05.2015248.32 Кб45matmodeli_Borisova_laba_1.doc
#
10.05.2015193.95 Кб10matsostavlyayuschaya_10.pdf
#
10.05.2015116.22 Кб12Med_genetika.doc
#
10.05.20151.79 Mб8Metodicheskie.Pdf
#
10.05.20153.17 Mб41Metodicheskie_k_kursovoy.doc
#
16.03.2016337.41 Кб25Metodicheskie_ukazania_k_SRS_I_PZ.doc
#
10.07.2019109.57 Кб1Metodicheskie_ukazania_po_napisaniyu_KKR_po_pra....doc
#
08.05.2019272.38 Кб1Metodicheskite_ukazania.doc
#
14.11.201996.77 Кб1metodichka-po-kr_OBSchAYa_DLYa_INSTITUTA_TIUB.doc