Metodicheskie

то все решения уравнения с достаточно малыми начальными условиями x(0) c, x(0) 0 есть периодические функции t. Каждое такое решение является

аналитической функцией параметра с.

Сформулированная теорема позволяет искать период периодического решения уравнения

x 2 x f (x, x)

в виде

и вводить новое время по формуле

не вводя малого параметра . При этом решение x( ) следует искать в виде ряда

k 1

Заметим, что если в уравнении не присутствует явно малый параметр и при этом в окрестности состояния равновесия выполнены условия теоремы Ляпунова, то для поиска периодического решения можно либо воспользоваться его разложимостью в ряд по начальным отклонениям с (формулой (8.10)), либо ввести малый параметр и использовать разложение по степеням малого параметра.

Пример 8.2. Найти приближенно периодическое решение уравнения Дуффинга

x x x3 0, x(0) c, x(0) 0 . (8.11)

Для решения задачи можно ввести малый параметр:

x y y y 3 y3 y y 2 y3 .

Здесь считаем малым. Теперь можно воспользоваться рассмотренной выше процедурой отыскания решения уравнения с малым параметром.

Заметим, что уравнение Дуффинга обладает аналитическим первым

замену переменных (8.9) и отыскивая решение в виде ряда (8.10) по степеням начального возмущения с.

Выполним замену (8.9). Тогда

53

Решение x( ) будем искать в виде ряда (8.10). После двукратного дифференцирования и подстановки этого ряда в уравнение (8.12) будем иметь:

Приравнивая коэффициенты при одинаковых степенях с в обеих частях последнего равенства, получим

Начальные условия для этих уравнений определяются так:

Для того, чтобы это уравнение имело периодическое решение, в его правой части должны отсутствовать резонирующие члены. Это имеет место лишь при h1 0 . Таким образом, для x2 получаем уравнение x2 x2 0 , из которого, с

учетом начальных условий (8.14), находим x2 ( ) 0 . Для x3 ( ) получаем уравнение

x3 x3 2h2 cos cos3 .

Запишем условия отсутствия резонирующих членов в правой части этого уравнения:

2

( 2h2 cos cos3 ) cos d 0,

0

2

( 2h2 cos cos3 )sin d 0.

0

Второе из выписанных соотношений всегда выполнено, а первое дает условие

( 34 2h2 ) 0 h2 83.

Итак, x3 ( ) следует искать из уравнения:

x3 x3 34 cos cos3 14 cos3 .

Отыскивая 2 -периодическое решение этого уравнения, удовлетворяющее начальным условиям x3 (0) 0, x3 (0) 0 , получим:

x3 ( ) 321 cos 321 cos3 .

54

Итак,

Сравнивая коэффициенты при 1 в обеих частях равенства (8.15), найдем

x1 x1 (4 x02 )x0 2h1x0

Учитывая вид x0 ( ) , получим

Найдем условия существования периодического решения у уравнения (8.16). Для этого запишем соотношения (8.7). Чтобы записать это соотношение, нужно последовательно умножить правую часть уравнения (8.16) на sin и cos и, проинтегрировав полученные выражения, приравнять интегралы в нулю. В данном случае (убедиться в этом самостоятельно) результатом реализации описанных операций будут соотношения:

c 4 1 c2 0, h1 0.4

Таким образом, c = 0 или ń 4 . Для c = 0 получаем тривиальное решение порождающего уравнения, которое остается решением исследуемого уравнения при любом . Для c = 4 получаем периодическое решение

55

16(sin 2cos 2 sin ) 16sin3 .

Итак, для x1 ( ) получаем уравнение

Общее решение последнего уравнения имеет вид:

x1 ( ) C1 cos C2 sin Asin 3 B cos3 .

Дважды дифференцируя это выражение и подставляя в (8.17), найдем значения

А и В:

A 2, B 0 x1 ( ) C1 cos C2 sin 2sin 3 .

Используя начальное условие x1 (0) 0 , находим C2 6 .

Итак, x1 ( ) C1 cos 6sin 2sin 3 . Теперь, приравнивая коэффициенты при 2 слева и справа в (8.15), найдем (учитывая, что h1 0 ):

x2 x2 2h2 x0 (4 x02 )x 2x0 x1x0 .

Подставляя найденные выше значения x0 ( ) и x1 ( ) , получим

x2 x2 8h2 cos 16sin 64sin cos2 32C1 sin cos2256cos 512cos3 256cos5 F .

Запишем условия существования периодического решения для последнего уравнения

Теперь окончательно можем записать x1 ( ) 6sin 2sin 3 , h2 4. Выпишем, наконец, приближенное решение исходного уравнения

Используя пакет Mathcad, сравним полученное решение с решением исходного уравнения методом Рунге-Кутта на периоде [0, 2 ].

56

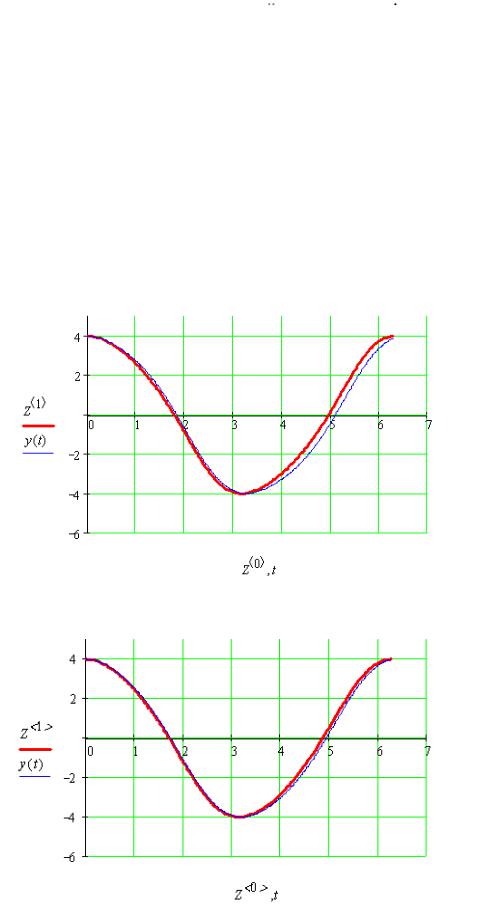
Исследуемое уравнение: x x (4 x2 )x

График для =0.07 (жирная линия – решение методом Рунге-Кутта)

График для =0.1 (жирная линия – решение методом Рунге-Кутта)

57

Задание 7

Методом Пуанкаре найти приближенно периодические решения данных

58

Библиографический список

1.Боровских А.В., Смагина Т.И.,Тананика А.А., Федотенко Г.Ф. Задания для самостоятельной работы студентов по дифференциальным уравнениям. Части 1 и 2. Издательство Воронежского университета. 1991. – 40 с.

2.Болгов В.А., Демидович Б.П., Ефименко В.А. и др. Сборник задач по математике для втузов. Специальные разделы математического анализа. М. "Наука". 1981. – 368 с.

3.Демидович Б.П. Лекции по математической теории устойчивости. М. "Наука". 1967. – 472 с.

4.Леонов Г.А., Буркин И.М., Шепелявый А.И. Частотные методы в теории нелинейных колебаний. Часть 1. Изд.-во Санкт-Петербургского университета. 1992. – 366 с.

5.Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. М. "Наука". 1970. –279 с.

6.Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М. "Наука".

1970. – 331 с.

7.Проскуряков А.П. Метод Пуанкаре в теории нелинейных колебаний. М. "Наука". 1977. – 256с.

8.Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения. Примеры и задачи. М. "Высшая школа". 1989.– 383 с.

9.Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. М. "Наука". 1980. – 230 с.

10.Федорюк М.В. Обыкновенные дифференциальные уравнения. М. "Наука".

1980. – 350 с.

11.Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. М. "Интеграл-пресс". 1998. – 207 с.

12.Хартман Ф. Обыкновенные дифференциальные уравнения. М. "Мир". 1970.

720 с.

59