
Metodicheskie
.Pdf
|
x x y; |
|
|
|
|
|
2. |
|
|
4 y |
|
|
|
|
|
|
|
|||
|
y 3x 0.5y |
|
|
|
|
. |
|
y |
2 |
|
2 |
||
|
|
|
|
|||
3.x x2 1 x x 0.
x2 1
x y;
y (x4 y2 4) y x.
|
|
2x |
|
|
|
x 0,1x 2 y |
|
|
; |
|
x2 1 |
|||
5. |
|
|
||
|
|
|
|
|
|
y x y. |
|
|
|
x y;
y x y 2y2 (x 2y).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
y |
2 |
); |
|
||
|
x y x(4 |
|
|
|
|
|
||||
7. |
|
|
|
|
|
|
|
|
|
|
|
y x y(4 |
x2 y2 ). |
||||||||
|
|
|
|
|
|
|
|
|
|
|
8.x (x2 ex2 2)x x 0.
9.x 2(x2 1) x 8x 0.
x2 2
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
x y 2x |
3 |
2 arctg |
|
|
|
; |
|||||
|
|
|
|
|||||||||
10. |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 0.2x. |
|
|
|
|
|
|
|
|
|
||
|
|
|
2 arctg x |
|
|
|
|
|||||
11. |
x 1 |
|
|
|
|
|
|
x x 0. |
||||
x |
2 |
1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
x y x 2arctg x;
12.
y 3x.
x y;
13.
y (3 2 x2 2 y2 ) y x.
|
|
|
|
|
|
|
|
14. |
x ( x2 x2 |
8)x x 0. |
|||||
15. |
x [1 (x2 |
3)e x2 ]x x 0. |
|||||
16. |
x (5x2 x2 |
8)x x 0. |
|||||
|
x y; |
|
|
|
|
||
17. |
|
|
|
|
|
2 y x. |
|
|
2 |
|
2 |
||||
|
y e 2 x |
y |
|
||||
|
|
|
|
|
|
||
|
|
|
|
17 2arctg x |
|
||||||||||||
18. |
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
x 0.8x 0. |
|||
|
x |
2 |
|
4 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
x 2x |
|
xe x |
|
y |
; |
|||||||||||
|
3 |
|
|
|
|
||||||||||||
19. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9x y ye |
x2 |
y2 |
. |
||||||||||||
|
y |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
2 |
|
|
2 |
|
|
x 2x |
|
xe x |
|
y |
; |
|||||||||||
|
3 |
|
|
|
|
||||||||||||
20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9x y ye |
x2 |
y2 |
. |
||||||||||||
|
y |
|
|
|
|
|
|
||||||||||
|
x y; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21. |
|
(4 y2 |
2 |
) y |
|
x. |
|||||||||||
|
y |
3x |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3x y x(x |
2 |
|
y |
2 |
); |
|||||||||||
22. |
|
|
|
||||||||||||||
|
x 3y y(x2 y2 ). |
||||||||||||||||
|
y |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23. |
x |
|
|
x4 1 |
|
|
x |
|
7 |
|
x 0. |
||||||
|
x4 x2 1 |
8 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
24.x x4 1 x 3x 0.
x4 2
x 4x y x(x2 y2 ); 25.
y x 4 y y(x2 y2 ).
26. x 2x2 1 x 2x 0. 2x2 3
x 3x y x3 x2 ;
y y 4x.
28. |
x (2 |
|
9 x |
|
|
|
)x |
1,2x 0. |
||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
x6 |
16 |
|||||||||
|
|
|
|
|
||||||
|
|
|
|
2 |
e |
x2 |
x 1; |
|||
29. |
x y (x 1) |
|
|
|||||||
|
|
|
|
|
|
|
|
|||
|
y 3x. |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
x 0.1x y; |
|
|
|
|
|||||
30. |
|
|
|
|
|
|
|
|
||
|
y x 2 y |
y3 y2. |
||||||||
|
x y; |
|
|
|
|
|
|
|
||
31. |
|
|
|
|
|
|
|
|
||
|
y x y(2 3x2 2y2 ). |
|||||||||
43

7. Метод Пуанкаре в теории нелинейных колебаний.
Неавтономные уравнения
Метод Пуанкаре предназначен для построения периодических решений нелинейных систем, дифференциальные уравнения которых содержат малый параметр . При этом предполагается, что обращение в нуль малого параметра не понижает порядка системы.
Метод Пуанкаре базируется на двух положениях:
1)порождающая система, т.е. система, получающаяся из исходной при=0, содержит периодические решения с некоторым периодом, частным случаем которых могут быть постоянные величины;
2)периодические решения исходной системы строятся при помощи подбора начальных данных всех входящих в систему неизвестных функций.
Начнем с решения следующей задачи: требуется найти периодическое решение периода T дифференциального уравнения:
|
|
|
|
x 2 x f (t). |
|
|
(7.1) |
|||
Заметим, что |
если |
решение уравнения |
(7.1) имеет период |
|
T, то |
|||||
x(t T ) x(t) x(t) 2 x(t) f (t T ) , то |
есть функция f(t) обязана быть |
|||||||||
периодической |
с периодом T. Выполнив |
в |
(7.1) замену времени |
t |
|
2 |
t и |
|||
|
||||||||||
|
|
|
|
|
|
|
1 |
|
T |
|
|
|
|
|
|
|
|
|
|
||
|
t T |
|
|
|
|
|
|
|
||
положив f1(t1) f |
1 |
|
, получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
|
|
|
|
|
||
|
|
(t 2 )T |
t T |
|
|
|||
f1(t1 |
2 ) f |
1 |
|
f |
1 |
T |
f (t T ) f (t) f1(t1) . |
|
2 |
2 |
|||||||
|
|
|
|
|
|
|||
То есть новая правая часть в новом времени будет 2 -периодической функцией. Поэтому правую часть уравнения (2.9.1) можно без ограничения общности считать 2 -периодической функцией.
Будем считать, что функция f(t) непрерывна и может быть разложена в сходящийся ряд Фурье
|
a0 |
|
|
|
f (t) |
(ak cos kt bk sin kt) . |
(7.2) |
||
|
||||
2 |
k 1 |
|
||
Пользуясь принципом суперпозиции, частное решение уравнения (7.1) будем искать в виде ряда
|
A0 |
|
|
|
x (t) |
( Ak cos kt Bk sin kt) . |
(7.3) |
||
2 |
||||
|
k 1 |
|
Дифференцируя ряд (7.3) почленно два раза и подставляя в (7.1), получим:
|
|
|
|
A |
|
|
|
|
||
k 2 ( Ak |
cos kt Bk |
sin kt) |
0 |
( Ak |
cos kt Bk |
sin kt) 2 |
|
|||
2 |
||||||||||
k 1 |
|
|
|
k 1 |
|
|
|
|||
|
a0 |
|
|
|
|
|
|
|
|
|
|
(ak cos kt bk sin kt). |
|
|
|
|
|
||||
|
|
|
|
|
|
|||||
2 |
k 1 |
|
|
|
|
|
|
|
||
44

Приравнивая коэффициенты при одинаковых гармониках слева и справа в последней формуле, будем иметь
A 2 |
a , A ( 2 k 2 ) a , B ( 2 k 2 ) b |
|
|||||||||||||||||
0 |
|
0 |
|
k |
|
|
|
|
|
|
k |
k |
|
|
|
k |
|
||
A |
a0 |
, A |
|
ak |
|
, B |
|
bk |
|
. |
|||||||||
|
|
|
|
|
|||||||||||||||
2 |
2 k 2 |
2 k 2 |
|
||||||||||||||||
0 |
|
|
|
|
k |
|
|
k |
|
|
|||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a cos kt b sin kt |
|
||||||||
x (t) |
0 |
|
|
|
k |
|
|
k |
|
|
|
|
(7.4) |
||||||
|
2 |
2 |
|
|
2 |
k |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
||||||
Из предположения о |
непрерывности f(t) |
следует, что ряд (7.4) можно |
|||||||||||||||||
почленно дифференцировать. Поэтому ряд (7.4) есть решение уравнения (7.1), если только 2 k 2 ни для какого k. Если же число целое ( k ), то соответствующее слагаемое в правой части (7.4) обращается в , и периодическое решение не существует.
Полученный результат можно было легко предугадать, если вспомнить, что при k линейное уравнение x 2 x acoskt bsin kt имеет решение вида x (t) t( Acos kt B sin kt) , не являющееся периодическим.
Из приведенных рассуждений вытекает следующий вывод: если не является целым числом, а f(t) – 2 -периодическая функция, то уравнение (7.1) всегда имеет 2 - периодическое решение, доставляемое формулой (7.4). Если же k – целое число, то 2 - периодическое решение уравнения (7.1) существует лишь в том случае, когда в разложении функции f(t) в ряд Фурье отсутствуют «резонирующие члены» ak и bk, то есть если:
|
|
1 |
2 |
|
|
|
1 |
2 |
|
|
|
ak |
|
|
f (t)cos ktdt 0, |
bk |
|
|
f (t)sin ktdt 0. |
(7.5) |
|||
|
|
||||||||||
|
|
0 |
|
|
|
0 |
|
|
Если k и выполнено условие (7.5), то уравнение (7.1) имеет бесконечное число 2 -периодических решений, которые даются формулой:
|
a |
|
a |
cos mt b sin mt |
|
||||
x(t) C1 cos kt C2 sin kt |
0 |
|
|
m |
|
|
m |
. |
|
2 |
2 |
|
|
2 |
m |
2 |
|||
|
|
m 1 |
|
|
|
|
|||
Если же k ( k N ) , то уравнение (7.1) имеет единственное периодическое
решение (7.4). |
|
|
|
|
|
|
|
|
|
|
Пример |
7.1. |
|
Существуют |
ли |
периодические решения |
уравнения |
||||
x 4x sin2 t ? |
|
|
|
|
|
|
|
|
|
|
Здесь 2 – целое число. |
|
|
|
|
|
|||||
|
a |
|
1 |
|
2 sin2 t cos 2tdt |
1 |
2 |
(1 cos 2t) cos 2tdt 0, |
|
|
|
|
2 |
|
|
||||||
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
b2 |
|
sin2 t sin 2tdt 0. |
|
|
|
||||
|
|
|
|
|
||||||
|
|
0 |
|
|
|
|
|
|||
Так как |
условия a2 0, b2 |
0 |
не |
выполняются, то периодического |
||||||
решения у рассматриваемого уравнения нет.
45

Аналитическая зависимость решений от параметров
Рассмотрим задачу Коши для системы уравнений
|
dxi |
f |
(t, x , x , |
, x , ), |
i 1, 2, |
, n |
|
||
|
|
|
|||||||
|
dt |
i |
|
1 2 |
n |
|
|
|
(7.6) |
|
|
|
|
|
|
|
|
||
|
xi (0) ai ( ), |
|
|
|
|
|
|||
где является параметром. |
|
|
|
|
|
|
|||
Теорема 7.1. Если в системе (7.6) функции |
fi непрерывны по переменной |
||||||||
t, а также функции fi и ai |
аналитические функции параметра в некоторой |
||||||||
окрестности точки 0 , то решение x(t) (x(t) Rn ) |
этой системы разлагается |
||||||||
в сходящийся при малых ряд по степеням параметра : |
|
||||||||
x(t, ) x (t) x (t) 2 x (t) |
n x (t) |
(7.7) |
|||||||
|
|
0 |
|
1 |
2 |
|
|
n |
|
Доказательство этой теоремы достаточно громоздко и здесь опущено.
Метод разложения решения по степеням малого параметра лежит в основе многих приемов исследования нелинейных колебаний с малой нелинейностью.
Рассмотрим следующую задачу: найти периодическое решение уравнения:
x 2 x f (t) F(t, x, x) |
(7.8) |
с 2 -периодическими по переменной t функциями f(t) и F (t, x, x) , считая, что 2 -периодическое решение x0 (t) порождающего уравнения:
(7.9)
существует и нам известно. Считая, что функция F (t, x, x) непрерывна по t и
является аналитической по переменным x и x , на основании приведенной выше теоремы, будем искать решение уравнения (7.8) в виде ряда (7.7) .
Разложим функцию F (t, x, x) в |
ряд по степеням (x x0 ),(x x0 ) в |
|||
окрестности точки x x0 , x x0 |
|
|
|
|
F (t, x, x) F (t, x , x ) F |
|
(x x ) |
||
|
||||
0 |
0 |
x |
|
0 |
|
|
|
x x0 |
|
|
|
|
|
x x0 |
Fx
|
(x x ) |
2 F |
|
(x x )2 |
|
(7.10) |
|
x2 |
|
||||
x x0 |
0 |
x x |
0 |
|
|
|
x x0 |
|
|
x x0 |
|
|
|
|
|
|
|
|
||
|
|
|
0 |
|
|
|
|
2 F |
|
|
(x x )(x x ) |
2 F |
|
(x x )2 |
|
|
x x |
|
x2 |
|
||||||
|
x x |
0 |
0 |
x x |
0 |
|
|||
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
x x0 |
|
|
|
x x0 |
|
|
Подставим в левую и правую части уравнения (7.8) вместо x, x и x ряд (7.7) и его соответствующие производные, а вместо F (t, x, x) выражение (7.10).
Сравнивая коэффициенты при одинаковых степенях в левой и правой частях полученного равенства, будем иметь:
46

|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
2 |
x0 |
f (t), |
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
x1 2 x1 F (t, x0 , x0 ), |
|
|
|
|
|||||||||
|
|
|
|
|
|
F |
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x |
2 x |
|
|
|
x |
|
x |
(7.11) |
|||||
|
|
|
|||||||||||
|
2 |
|
|
2 |
|
x |
|
1 |
x |
|
1 |
|
|
|
|
|
|
|
|
x x0 |
|
|
x x0 |
|
|||
|
|
|
|
|
|
|
x x0 |
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Каждое следующее уравнение (7.11) будет содержать в правой части только известные функции, найденные из предыдущих уравнений. Поэтому все решения уравнений (7.11) могут быть последовательно найдены.
Если мы хотим найти 2 -периодическое решение уравнения (7.8), то все члены ряда (7.7) должны быть 2 -периодическими функциями. Значит каждое из уравнений (7.11) должно иметь 2 -периодическое решение. Выясним, когда эти условия выполняются.
1)n, где n – какое-либо целое число. Тогда 2 -периодическое решение у порождающего уравнения (7.9) и всех остальных уравнений в (7.11) существует всегда. Все эти решения могут быть найдены так, как было описано выше.
2)n, n N . Тогда порождающее уравнение (7.9) имеет периодическое решение лишь при условии равенства нулю коэффициентов an и bn в
разложении функции f(t) в ряд Фурье, то есть при выполнении условий:
2 |
|
2 |
|
|
|
f (t)cos ntdt 0, |
|
f (t)sin ntdt 0 . |
(7.12) |
0 |
|
0 |
|
|
Если условия (7.12) выполнены, то порождающее уравнение имеет решение:
|
x0 (t) C10 cos nt C20 sin nt 0 (t) . |
|
|
Для определения |
x1 (t) имеем второе уравнение из (7.11). Оно будет иметь |
||
периодическое решение, если |
|
|
|
2 |
|
2 |
|
F(t, x0 , x0 )cos ntdt 0, |
F(t, x0 , x0 )sin ntdt 0 . |
(7.13) |
|
0 |
|
0 |
|
Уравнения |
(7.13) содержат C10 ,C20 , которые, |
вообще говоря, |
|
определяются из этой системы. Если C10 ,C20 удовлетворяют системе (7.13), то
все решения второго уравнения в (7.11) будут периодическими с периодом 2 и будут иметь вид:
x1 (t) C11 cos nt C21 sin nt 1(t) . |
(7.14) |
При этом C11,C21 опять определяются из двух условий, аналогичных (7.12) и |
|
(7.13), для третьего уравнения из (7.11). И так далее. |
|
Как мы видим, в случае 2) (резонансный случай), |
вообще говоря, не |
любому 2 -периодическому решению порождающего уравнения соответствует периодическое решение уравнения (7.8), задаваемое рядом (7.7), которое при0 сходится к решению порождающего уравнения. Существование подобного решение нужно доказать. Такое доказательство составляет
47

содержание известной теоремы Пуанкаре. Но это доказательство очень громоздко и здесь не приводится.
Пример 7.2. Найти приближенно периодическое решение уравнения:
x 2x sin 2t x2 , |
где – малый параметр. |
||
Решение будем искать в виде ряда по степеням малого параметра, то есть |
|||
в виде |
|
|
|
|
x(t) x (t) x (t) 2 x (t) . |
||
|
0 |
1 |
2 |
Тогда
x(t) x0 (t) x1(t) 2 x2 (t) 
x(t) x0 (t) x1(t) 2 x2 (t) 
Подставим ряды в исходное уравнение
(x (t) x (t) 2 x (t) |
) 2(x (t) x (t) 2 x (t) |
|
) |
||||||||||||
0 |
1 |
|
2 |
|
|
|
0 |
|
1 |
|
2 |
|
|
|
|
sin 2t (x2 |
2 x2 4 x2 |
2 x x 2 2 x x |
2 3x x |
|
) |
||||||||||
|
0 |
1 |
|
2 |
|
0 |
1 |
0 |
2 |
1 |
2 |
|
|
||
Приравняем коэффициенты при одинаковых степенях |
параметра в левой и |
||||||||||||||
правой частях последнего равенства: |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
0 |
|
x0 2x0 |
sin 2t |
|
|
|
|
|
|||
|
|
|
|
1 |
|
x1 2x1 |
x02 |
|
|
|
|
|
(7.15) |
||
|
|
|
|
2 |
|
|
2x |
2x x |
|
|
|
|
|||
|
|
|
|
|
x |
|
|
|
|
|
|||||
|
|
|
|
|
|
2 |
2 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Поскольку |
2 , |
порождающее |
уравнение |
|
имеет |
|
|
единственное |
|||||||
периодическое решение, которое будем искать в виде: |
|
|
|
|
|
||||||||||
|
|
|
|
x0 Asin 2t B cos 2t . |
|
|
|
|
|
||||||
После двукратного дифференцирования и подстановки в первое уравнение
(7.15), получим:
4Asin 2t 4B cos 2t 2 Asin 2t 2B cos 2t sin 2t
A 12 , B 0 x0 12 sin 2t.
Для отыскания x1 имеем уравнение
x1 2x1 cos2 2t 12 1 cos 4t
Будем искать x1 в виде:
x1 M N cos 4t L sin 4t
После двукратного дифференцирования и подстановки в уравнение получим:
14N cos 4t 14Lsin 4t 2M 12 12 cos 4t N 281 , L 0, M 14.
Итак, x1 14 281 cos 4t .
Подставим найденные функции x0 и x1 в правую часть последнего уравнения (7.15). Тогда оно примет вид
48

x |
2x |
|
2 |
cos 2t sin 4t |
1 |
sin 6t |
1 |
sin 2t. |
(7.16) |
|
|
|
|||||||
2 |
2 |
7 |
7 |
7 |
|
|
|||
|
|
|
|
||||||
Будем искать решение последнего уравнения в виде
x2 Asin 6t B cos 6t C sin 2t D cos 2t .
После двукратного дифференцирования последнего выражения и подстановки в уравнение (7.16), находим
A 2661 , B 0,C 421 , D 0 x2 2661 sin 6t 421 sin t.
Итак, справедливо приближенное равенство
x(t) |
1 |
sin 2t ( |
1 |
|
1 |
cos 4t) 2 ( |
1 |
sin 6t |
1 |
sin 2t) . |
(7.17) |
|
2 |
4 |
28 |
266 |
42 |
||||||||
|
|
|
|
|
|
|
Используя пакет Mathcad, сравним полученное решение (7.17) с точным решением исходного уравнения на периоде [0, 2 ] . Для этого найдем для
решения (7.17) значения x(0) и x(0) , после чего найдем решение исходного
уравнения с заданными начальными условиями, например, методом РунгеКутта. Результаты расчетов приведены ниже.
Исследуемое уравнение: x 2x sin 2t (x)2
: 0.5
y(t) : 1 sin(2 t) 0.25 0.035714cos(4 t) |
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
0.00376sin(6 |
t) 0.02381sin(2t) |
||||
|
|
|
|
|||||||
g(t) : |
d |
|
y(t) |
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
t : 0,0.01 .. 2 |
|
|
|
|
|
|||||
y(0) |
|
|
|
|
x1 |
|
|
|
||
x : |
|
D( , x) : |
|
(x1) |
2 |
sin(2 |
|
|||
g(0) |
|
|
2 x0 |
|
) |
|||||
Z : rkfixed (x,0, 2 ,300, D) |
|
i : 0..300 |
|
|||||||
49
x1 |
|
|
|
|
|
|
|
|
(x ) 2 |
sin(2 ) |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0..300 |
|
|
|
|
|
|
|
|
етодом Рунге-Кутта) |
|
|
|
|
|
|
||
|
|
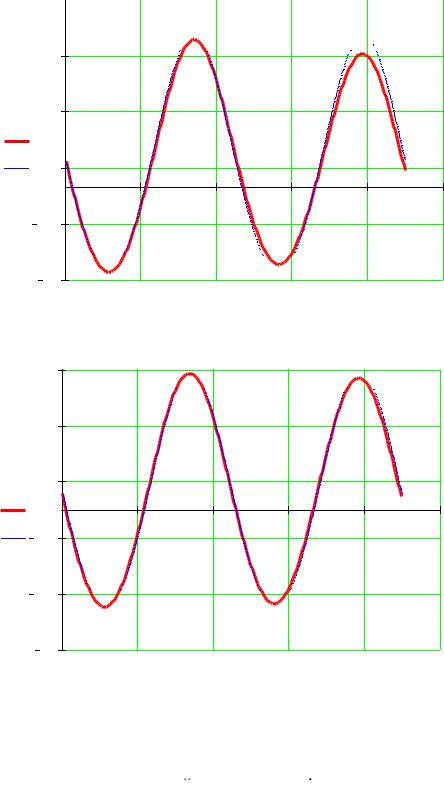
График для =0.5 (жирная линия – решение методом Рунге-Кутта) |
||||||
t) |
|
|
|
|
|
|
|
|
.02381sin(2t) |
|
0.56 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Z 1 |
0.32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(t) |
|
|
|
|
|
|
|
|
|
0.08 |
|
|
|
|
|
|
|
|
0 |
1.4 |
2.8 |
4.2 |
5.6 |
7 |
5 |
6 |
7 |
0.16 |
|
|
|
|
|
|
|
|
|
|
|
|||
x1 |
|
|
|
|
|
|
|
|
(x ) 2 |
sin(2 ) |
0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
Z 0 |
|
|
|
0..300 |
|
|
|
t |
|
|
||
|
|
|
|
|
|
|
||
|
|
График для =0.3 (жирная линия – решение методом Рунге-Кутта) |
||||||
етодом Рунге-Кутта) |
|
|
|
|
|
|
||
етодом Рунге-Кутта)
Z 1
y(t)
5 |
6 |
7 |
0.6 |
|
|
|
|
|
0.36 |
|
|
|
|
|
0.12 |
|
|
|
|
|
0 |
1.4 |
2.8 |
4.2 |
5.6 |
7 |
0.12 |
|
|
|
|
|
0.36 |
|
|
|
|
|
0.6 |
|
|
|
|
|
|
|
|
Z 0 t |
|
|
Автономные уравнения
етодом РунгеПусть-Куттазадано) уравнение, правая часть которого не зависит явно от t:
x 2 x F(x, x) . |
(8.1) |
Отсутствие t в правой части приводит к усложнению задачи, так как период искомого решения оказывается неизвестным. Он будет, вообще говоря, зависеть от параметра .
Для решения задачи в этом случае нужно преобразовать уравнение к новой независимой переменной так, чтобы по новой переменной уравнение уже
50

имело постоянный период, а уже затем искать решение в виде ряда по параметру .
Предварительно выполним в (8.1) замену времени, положив t1 t . Тогда в новом времени уравнение примет вид:
x x F1 (x, x) , |
|
|
|
|
(8.2) |
|||
|
|
|
|
|
|
dx |
|
|
где производные x и x вычислены по переменной t1, а F1(x, x) F x, |
. |
|||||||
|
||||||||
|
|
|
|
|
|
dt1 |
||
При =0 порождающее уравнение |
x x 0 имеет |
2 -периодическое |
||||||
решение вида x(t1 ) C cos(t1 t0 ) , |
удовлетворяющее начальным |
условиям |
||||||
x(t0 ) C, x(t0 ) 0 . Периодические |
решения |
уравнения |
(8.2), |
если |
они |
|||
существуют, будут иметь период |
2 ( ) , |
причем ( ) |
– аналитическая |
|||||
функция и ( ) 0 при 0 . Пусть: |
|
|
|
|
|
|
||
|
|
|
|
( ) |
2 |
|
n |
. |
|
|
|
|
||||
|
|
|
|
|
|
1 |
2 |
|
|
n |
|
|
|
|
|
|
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 ( ) 2 (1 h h 2 |
h n |
|
), ăäĺ h |
i |
. |
|
|||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
2 |
|
n |
|
|
|
i |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Преобразуем уравнение (8.2) так, чтобы его решение x(t, ) |
имело постоянный |
|||||||||||||||
период 2 . Этого можно добиться заменой переменных: |
|
|
|
|
||||||||||||
|
|
|
t (1 h h 2 |
h n |
) |
|
|
|
|
(8.3) |
||||||
|
|
|
1 |
1 |
|
2 |
|
n |
|
|
|
|
|
|
|
|
Действительно, если t1 меняется от 0 до 2 ( ) , то меняется от 0 |
до 2 . |
|||||||||||||||
В новых переменных уравнение (8.2) приобретает вид: |
|
|
|
|
||||||||||||
|
|
x (1 h h 2 |
|
h n |
|
)2 x |
|
|
|
|
|
|
||||
|
|
|
1 |
2 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
(1 h h 2 |
|
h n |
|
)2 |
|
|
|
|
|
(8.4) |
||||
|
|
|
1 |
2 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
F (x,(1 h h 2 |
h n |
|
) 1 x), |
|
|
|
|
|
||||||
|
|
1 |
|
1 |
2 |
|
n |
|
|
|
|
|
|
|
|
|
где все производные вычислены по переменной . |
|
|
|
|
|
|
||||||||||
Периодическое решение уравнения (8.4) будем искать в виде ряда |
||||||||||||||||
|
|
x( , ) x ( ) x ( ) |
n x ( ) |
, |
|
|
|
(8.5) |
||||||||
|
|
|
0 |
|
1 |
|
|
|
n |
|
|
|
|
|
|
|
где все xi ( ) – |
2 -периодические функции переменной . Подставляя (8.5) в |
|||||||||||||||
уравнение (8.4), получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x ( ) x ( ) 2 x ( ) |
(1 h h 2 |
|
)2 |
|
|
|
|
|
|
|||||||
0 |
1 |
2 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
(x ( ) x ( ) 2 x ( ) |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(1 h h |
2 |
)2 F [(x ( ) x ( ) 2 x ( ) |
),(1 h h 2 |
) 1 |
||||||||||||
1 |
2 |
|
1 |
0 |
|
1 |
|
|
2 |
|
|
1 |
|
2 |
|
|
(x ( ) x ( ) 2 x ( ) )] |
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Приравнивая коэффициенты при одинаковых степенях параметра в левой и правой частях последнего равенства, последовательно получим:
51

x0 x0 |
0 x0 C cos( t0 ) |
|
|
x1 x1 |
2h1x0 F1 (x0 , x0 ) |
(8.6) |
|
2h1C cos( t0 ) F1(C cos( t0 ), C sin( t0 )) |
|||
|
|||
Для того, чтобы второе уравнение в (8.6) имело периодическое решение, необходимо и достаточно, чтобы в его правой части отсутствовали резонирующие члены, то есть чтобы выполнялись условия:
2 |
|
F1[C cos( t0 ), C sin( t0 )]sin( t0 )d 0 |
|
0 |
|
2 |
|
{ 2h1C cos2 ( t0 ) F1[C cos( t0 ), C sin( t0 )]cos( t0 )}d |
(8.7) |
0 |
|
2 |
|
2 h1C F1[C cos( t0 ), C sin( t0 )]cos( t0 )d 0
0
Первое из этих уравнений дает возможность найти С (начальное условие периодического решения), а второе – найти h1. Таким образом, будет
приближенно определен период искомого периодического решения:
2 ( ) 2 (1 h1 ) .
Зная С и h1, можно определить x1 ( ) и, если это необходимо, x2 ( ) , x3 ( ) и так
далее.
Пример 8.1. Определить решения порождающего уравнения, к которым
при 0 приближаются периодические решения уравнения: |
|
x x x(9 x2 ) |
(8.8) |
Решения порождающего уравнения имеют вид x(t) C cos(t t0 ) . |
Для |
определения искомых значений С воспользуемся первым из уравнений (8.7):
2 |
|
C |
2 |
|
|
C(9 C 2 cos2 (t t0 ))sin2 (t t0 )dt 0 C(9 |
|
) 0 |
|
|
|
|||
0 |
4 |
|
||
|
|
|
|
|
C1 0,C2,3 6.
При С=0 получаем тривиальное решение x 0 порождающего уравнения, которое остается решением уравнения (8.8) при любом .
При C2,3 6 получаем x 6cos(t t0 ) .
Теорема Ляпунова и несколько практических замечаний
Теорема Ляпунова выделяет класс систем, у которых в некоторой окрестности состояния равновесия существует периодическое решение и дает
метод отыскания этого решения. |
|
Теорема 8.1. Если уравнение x 2 x f (x, x) обладает |
аналитическим |
первым интегралом H (x, x) const , причем разложение H (x, x) |
в окрестности |
точки x 0, x 0 начинается с членов второго порядка малости: |
|
52
