
Математика Сам раб 140400 140100
.pdf81
1.Алгебра случайных событий.
2.Случайные величины. Законы распределений. Числовые характеристики. 3.Математическая статистика. Оценки числовых характеристик. Определения закона распределения по выборке. Критерии согласия.
4.Математическая статистика: оценка коэффициента корреляции по выборочным данным, уравнение линейной регрессии.
Список литературы [2,5,12, 15, 18 ]
Номера задач указаны согласно сборнику задач по математике для втузов , часть 3 « Теория вероятностей и математическая статистика» под
ред. Ефимова А.В.М., « Наука», 1990 (№ 15 в списке литературы, имеется в библиотеке в достаточных количествах)
1. Основные понятия. Алгебра событий. № 14.1, 14.68, 14.69, 14.70,14.5, 14.7 (14.148), 14.80,4.87, 14.139, 14.191, 14.198, 14.207, 14.208-14.211, 14.214, 14.226, 14.227, 14.231, 14.233, 14.243.
2.Случайные величины. Законы распределений. Основные характеристики.
№ 14.312, 14.313, 14.323, 14.352, 14.353, 14.354, 14.278, 14.279, 14.294, 14.297, 14.300, 14.365-14.367,14.536-14.539, 14.558, 14.559, 14.560, 14,570
3.Данные для статистической обработки (задания № 3, 4) каждый
студент получает от преподавателя или получает самостоятельно
(утверждает у преподавателя). Подробное рассмотрение в электронном пособии (№ 18 в списке литературы)
Лабораторная работа № 1
« Статистическое описание результатов наблюдений. Числовые оценки выборочного распределения. Интервальные оценки для математического ожидания и дисперсии. Проверка гипотезы о виде распределения»
1.Получите выборку из n чисел
2.Постройте вариационный ряд (упорядочите элементы выборки по величине). При
этом можно использовать соответствующую команду на панели инструментов Excel.
3 .Представьте выборку в виде группированного статистического ряда (с.178181)

82
определите размах выборки w xmax xmin
определите число интервалов группировки одним из способов:
а) Способ 1: выбираете число интервалов k 
 n , а затем находите шаг (ширину
n , а затем находите шаг (ширину
интервала группировки) |
b |
w |
, б) |
Способ 2: выбираете шаг (ширину |
||||||||
|
||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
xmax xmin |
|
|
|
w |
|
|
|
интервала группировки) |
по формуле |
|
1 3,2lg n |
1 |
3,2lg n . |
|
||||||
|
|
|
|
|
xmin (xmin b) |
|
|
|
||||
Определите границы интервалов группировки (x |
b) (x |
2b) |
, и так далее до |
|||||||||
|
|
|
|
|
min |
|
|
min |
|
|
|
|
тех пор, пока наибольший элемент выборки не попадет в последний интервал ( наилучшая ситуация, если он точно совпадает с верхней границей последнего интервала)
Найдите середину каждого интервала xi
Определите частоты ni - число элементов выборки, содержащихся в каждом i -
м интервале. При этом элемент, совпадающий с верхней границей интервала,
условимся относить к следующему интервалу.
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдите накопленные частоты n j . |
При этом сумма частот по всем |
||||||||||||
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
интервалам должна совпадать с объемом выборки |
ni |
n . Если сумма |
|||||||||||
|
|
|
|
|
|
|
|
i 1 |
|
|
||||
|
частот по всем интервалам не совпадает с объем выборки, то следует |
|||||||||||||
|
проверить, правильно ли найдены частоты. |
|
|
|
|
|
|
|
||||||
|
|
|
ni |
|
|
|
|
|
|
|
|
|
|
|
Найдите относительные частоты |
n , |
которые служат оценкой вероятности |
||||||||||||
|
попадания элемента выборки в данный интервал |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
i |
|
n j |
|
|
|
||
|
Найдите относительные накопленные частоты |
. |
|
|
||||||||||
|
|
Значения накопленных |
||||||||||||
|
|
|
|
|
|
|
j 1 |
n |
|
|
||||
|
частот служат оценкой функции распределения и определяют эмпирическую ( |
|||||||||||||
|
|
|
|
|
|
|
|
|
ni |
|
||||
|
выборочную) функцию распределения |
Fn (x) |
||||||||||||
|
|
|
||||||||||||
|
|
|
|
x |
x n |
|||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
Все полученные характеристики заносим в таблицу, которую называют
статистическим рядом ( табл. 1.1 на стр. 181)

83
Номер |
Границы |
Середина |
Частота |
Накопленная |
Относител |
Накопленная |
||||
интервала |
интервала |
Интервала |
ni |
Частота |
ная частота |
Относитель- |
||||
|
|
xi |
|
ni |
|
ni |
|
ная частота |
||
|
|
|
|
|
|
n |
|
ni |
|
|
|
|
|
|
|
|
|
|
n |
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Представить выборку графически (стр. 182-183)
строим полигон частот- ломаную с вершинами в точках ( xi , ni )
строим полигон относительных частот- ломаную с вершинами в точках ( xi , ni n
)
строим гистограмму - кусочно-постоянную функцию, которая на каждом
ni
интервале группировки принимает значение b . Площадь ступенчатой фигуры под графиком гистограммы равна объему выборки n .
Полигон относительных частот является статистическим аналогом функции плотности вероятности. Гистограмма и полигон частот отличаются от указанной
характеристики растяжением в n раз. Поэтому все данные функции также являются характеристиками закона распределения генеральной совокупности f (x) .
Примечание. Все перечисленные выше операции можно провести вручную или с использованием компьютерных программ. Самое доступное математическое
обеспечение |
– |
Microsoft |
Excel |
при |
помощи |
команд: |
сервис анализ данных гистограмма . |
При |
этом |
карманы |
(интервалы |
||
группировки) надо задать отдельно. |
|
|
|
|
||
Пример выдачи данных. |
|
|
|
|
|
|
4,05001 |
Размах |
Шаг |
Интервалы группировки |
|
||
3 |
|
|
|
|
|
|
6,38965 |
9,53838 |
0,9538 |
|
|
|
|
2 |
7 |
|
|
|
|
|
6,63373 |
|
|
5,0038 |
|
|
|
3 |
|
|
|
|
|
|
6,76392 |
|
|
5,9576 |
|
|
|
7 |
|
|
|
|
|
|
6,91932 |
|
|
6,9114 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
84 |
|
7,09546 |
|
|
|
7,8652 |
5 |
|
|
|
|
7,32934 |
|
|
|
8,819 |
2 |
|
|
|
|
7,45222 |
|
|
|
9,7728 |
8 |
|
|
|
|
7,63468 |
Карман Частот |
Интегральный |
10,7266 |
|
6 |
а |
|
% |
|
7,64757 |
5,0038 |
1 |
1,00% |
11,6804 |
4 |
|
|
|
|
7,69012 |
5,9576 |
0 |
1,00% |
12,6342 |
7,83211 |
6,9114 |
3 |
4,00% |
13,58 |
7,88450 |
7,8652 |
8 |
12,00% |
|
2 |
|
|
|
|
8,05237 |
8,819 |
15 |
27,00% |
|
2 |
|
|
|
|
8,08335 |
9,7728 |
23 |
50,00% |
|
8 |
|
|
|
|
8,09687 |
10,7266 |
14 |
64,00% |
|
3 |
|
|
|
|
8,12840 |
11,6804 |
19 |
83,00% |
|
1 |
|
|
|
|
8,14257 |
12,6342 |
11 |
94,00% |
|
5 |
|
|
|
|
8,36074 |
13,58 |
5 |
99,00% |
|
8,39876 |
Еще |
1 |
100,00% |
|
4 |
|
|
|
|
8,41871
2
8,45298
6
8,49555
9
Полигон частот
Частота n i
25
20
15
10
5
0
4 |
6 |
8 |
10 |
12 |
14 |
16 |
Середина интервала
85
5. Определяем основные числовые характеристики выборочного распределения
Оценкой математическоо ожидания является выборочное среднее
|
n |
|
|
|
xi |
|
|
x |
i 1 |
, |
|
n |
|||
|
|
если каждый элемент выборки встречается один раз.
Если элемент выборки xi имеет частоту ni , то выборочное среднеенаходят по формуле
|
n |
|
|
|
ni xi |
|
|
x |
i 1 |
. |
|
n |
|||
|
|
В том случае, если выборка группированная, то вместо элемента выборки в этой формуле берут середину интервала, а за частоту берут число элементов, попадающих в данный интервал.
|
~ |
|
|
Выборочная дисперсия S 2 x Dx |
служит оценкой дисперсии распределения |
генеральной совокупности и определяется по следующим формулам
Если каждый элемент выборки встречается только один раз (ni 1) и объем выборки достаточно велик ( n 30), то следует использовать формулу
|
|
n |
|
n |
|
n |
n |
|
|
|
(xi x)2 |
|
x2i nx 2 |
|
n x2i ( xi )2 |
|
|
|
S 2 x |
i 1 |
|
i 1 |
|
i 1 |
i 1 |
. |
n |
n |
|
n |
|||||
|
|
|
|
|
|
|||
Для выборок малого объема несмещенную (исправлннную) дисперсию следует вычислять по формуле
|
|
n |
|
|
|
(xi x)2 |
|
|
S 2 x |
i 1 |
|
n 1 |
|||
|
|
Если частота каждого элемента ni , то для выборок большого объема следует использовать формулу
|
n |
|
n |
n |
|
|
ni (xi x)2 |
|
n ni x2i ( ni xi )2 |
|
|
S 2 x |
i 1 |
|
i 1 |
i 1 |
. |
n |
|
n2 |
|||
|
|
|
|
||
Для группированных выборок в этой формуле нужно использовать середину интервала и число элементов, попадающих в этот интервал.

86
Для вычислений вручную подробнее см. стр. 189-191
Все перечисленные операции можно выполнить в Excel согласно командам
сервис анализ данных описательная статистика
Пример выдачи данных:
Столбец1
Среднее |
9,899346449 |
Стандартная ошибка |
0,177148981 |
Медиана |
9,79959739 |
Мода |
11,52953362 |
Стандартное |
1,771489807 |
отклонение |
|
Дисперсия выборки |
3,138176135 |
Эксцесс |
0,060472776 |
Асимметричность |
-0,273471727 |
Интервал |
9,531831893 |
Минимум |
4,050012901 |
Максимум |
13,58184479 |
Сумма |
989,9346449 |
Счет |
100 |
Уровень |
0,351502073 |
надежности(95,0%) |
|
6. Интервальные оценки ( доверительные интервалы) параметров распределения (
стр.230-234)
Доверительным интервалом называют интервал, содержащий истинное значение
параметра с заданной вероятностью P 1 , которую называют доверительной
вероятностью.
В тех случаях, когда дисперсия генеральной совокупности неизвестна, а получена ее оценка по указанным выше формулам, доверительный интервал для математического ожидания имеет вид:
P(x Snx t1 2 (n 1) M x x Snx t1 2 (n 1)) 1
Здесь - уровень значимости. Ширина доверительного интервала характеризует точность оценивания или стандартную ошибку sxn t1 / 2 (n 1) и зависит от
объема выборки и доверительной вероятности (уровня значимости). С увеличением объема выборки ширина доверительного интервала уменьшается (точность оценивания
87
возрастает), а по мере приближения доверительной вероятности к единице (приближении уровня значимости к нулю) ширина доверительного интервала увеличивается ( точность оценивания падает).
Здесь t |
(n 1) квантиль распределения Стьюдента ( стр. 225-226, таблица на стр. |
1 |
2 |
414 ) или в Excel на панели инструментов находите статистические функции и распределение Стьюдента.
Доверительный интервал для дисперсии в том случае, если математическое ожидание неизвестно, а оценки получены по выборке, находим согласно соотношению
|
|
|
P( |
|
nSx2 |
2 |
nSx2 |
) 1 |
||
|
|
|
2 |
(n 1) |
2 (n 1) |
|||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
Здесь |
2 |
(n 1) , |
2 |
(n 1) квантили распределения |
2 ( стр.224-225, таблица |
|||||
|
1 |
2 |
2 |
|
|
|
|
|
|
|
на стр 412 ) или в Excel.
функции статистическиефункции "хи квадрат распределение".
7. Проверка гипотезы о виде распределения генеральной совокупности
На следующем этапе работы по виду полигона частот (гистограммы ) и полученным значениям числовых характеристик выдвигаем гипотезу о виде распределения генеральной совокупности и проверяем соответствие данной гипотезы эмпирическим данным.
После того, как выдвинули гипотезу, находим теоретические частоты, соответствующие предполагаемому распределению:
|
xi 1 |
niT npi |
n f (x)dx nbf (xi ) n(F (xi 1) F (xi )) |
xi
1.Нормальный закон распределения
Если полигон частот является симметричным, а числовые характеристики выборки удовлетворяют особенностям этого распределения
xmax xmin |
x, |
xmax xmin |
Sx , |
|
|
||||
2 |
6 |
|||
|
|

88
то делаем предположение, что выборка получена из нормально распределенной генеральной совокупности. Этот закон имеет два параметра, оценки которых находим по выборке:
x M x - выборочное среднее приравниваем к математическому ожиданию,
Sx - выборочное среднеквадратичное отклонение (стандарт) приравниваем к его теоретическому значению. Функция плотности вероятности для нормированной
|
|
|
xi x |
|
|
1 |
|
|
|
ti2 |
|
|
|
|
|
приводят по таблице на стр.408 (ti ) |
|
|
|
|
|||||
переменной |
ti |
|
|
|
|
e |
2 . |
|||||
|
|
|
||||||||||
2 |
||||||||||||
Sx |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
nT |
|
nb |
(t |
) |
|
||||
Теоретическую частоту находим по формуле i |
|
|
i |
|
|
|
Sx |
|
|
2. Показательный закон. Этот закон характеризуется одним параметром , оценку которого находим по методу моментов, приравнивая выборочное среднее к
|
M x x |
1 |
|
|
1 |
|
|
теоретическому значению математического ожидания: |
|
, |
x . |
||||
|
|
||||||
Особенностью распределения является равенство единице коэффициента вариации
Sx |
1. Теоретические частоты находим по формуле |
niT nb e xi |
|
x |
|||
|
|
1.Гамма распределение характеризуется двумя параметрами, оценки которых находим, приравнивая теоретические и выборочные моменты с учетом того, что
|
M X |
a |
, D X |
a |
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|||||||||
|
|
2 |
, коэффициент вариации |
M X . |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
M X x, |
|
|
, |
|
|
|
s |
|
1 |
|
, a |
x 2 |
|
|
|
|
a |
|
|||||||||
|
|
|
|
|
s |
x |
V |
|
, |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
a |
|
|
|
s2 |
|
|
|
x |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Оценку теоретической частоты находим по формуле |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
a x a 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
T |
nb |
|
|
xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ni |
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г (a ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Г (n) (n 1)! |
|
|
|
Значение гамма-функции находим по таблице (например, Г. Корн, Т. |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Г (a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
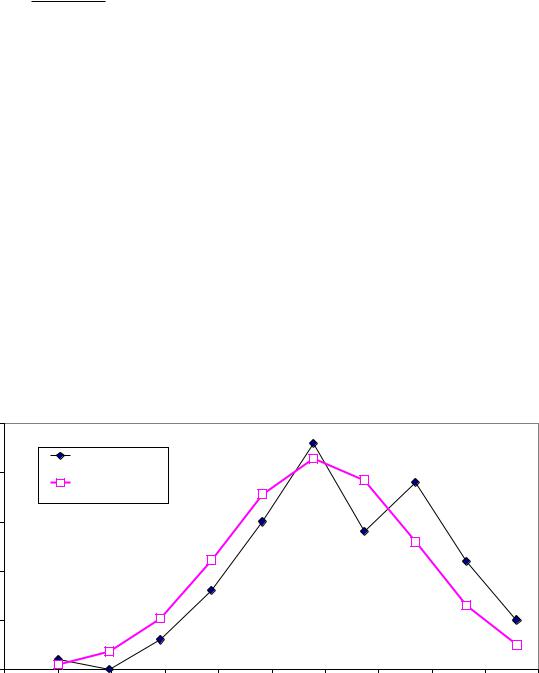
Корн Справочник по математике). |
Г (x) t x 1e t dt, |
|
Г (x) (x 1)Г (x 1) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
89 |
|
|
|
|
|
Полученные теоретические частоты наносим на полигон частот. Если согласие |
||||||||||||
между эмпирическими и предполагаемыми теоретическими частотами визуально |
||||||||||||
достаточно хорошее, то проводим проверку выдвинутой гипотезы по критерию 2 |
||||||||||||
(стр. 278-281). При этом выборочное значение статистики критерия находят по формуле |
||||||||||||
выб2 |
r |
(n nT )2 |
|
r - число интервалов с учетом того, что ni |
5 . Если это |
|||||||
|
i |
T i . |
Здесь |
|||||||||
|
i 1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
условие не выполняется, то объединяем соседние интервалы. |
Теоретическое значение |
|||||||||||
статистики критерия находим по таблице на стр. 412 : 12 (r l 1) 12 (k) . В этом |
||||||||||||
выражении k r l 1 |
– число степеней свободы. Здесь l - это число параметров |
|||||||||||
распределения, оцениваемых по выборке. Так для показательного закона l 1, для |
||||||||||||
нормального закона и гамма-распределения l 2 . |
|
|
|
|
||||||||
Если выполняется условие |
выб2 |
12 (k) , |
то выдвинутая гипотеза не противоречит |
|||||||||
опытным данным на заданном уровне значимости |
|
и не может быть отвергнута. |
||||||||||
Далее приведен пример сравнения эмпирического распределения, полученного по |
||||||||||||
выборке, и нормального распределения |
|
|
|
|
|
|||||||
параметрами x 9,899; |
s 1,771. |
|
|
|
|
|
||||||
|
|
Полигон частот: сравнение эмпирического и предполагаемого |
|
|||||||||
|
|
|
теоретического нормального распределений |
|
|
|||||||
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эмпирические |
|
|
|
|
|
|
|
|
|
20 |
|
данные |
|
|
|
|
|
|
|
|
|
|
|
нормальное |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
распределение |
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
Частота |
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
5 |
6 |
7 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
|
|
|
Значение случайной величины |
|
|
|
|
|||
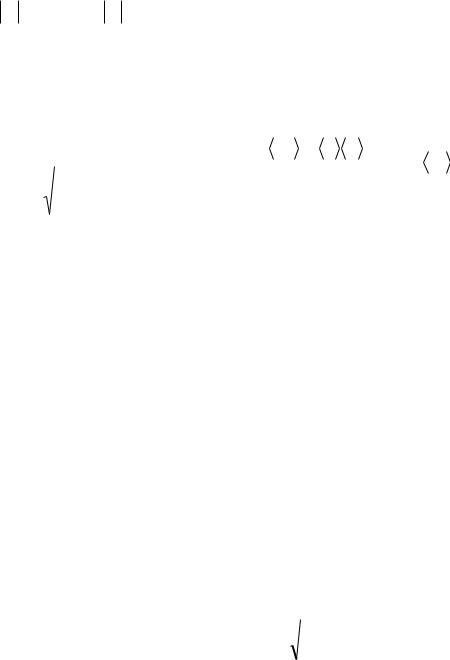
90
ЛАБОРАТОРНАЯ РАБОТА № 2.
ВЫБОРОЧНЫЙ КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
Коэффициент корреляции двух случайных величин определяет степень линейной корреляционной зависимости между ними
r |
M ( X M X )(Y M Y ) |
|
|
M XY M X M Y |
. |
|
|
||||
xy |
x y |
|
x y |
||
|
|
||||
rxy 1. Если rxy 1, то случайные величины связаны точной линейной зависимосью.
Выборочный коэффициент корреляции служит оценкой коэффициента корреляции и определяется выражением
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
(xk x)(yk y) |
xy x y |
|
|||||
rxy |
|
|
k 1 |
|
|
|
|
|
, где означает усреднение. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x y |
||||
n |
|
n |
|
|||||||
|
|
|
(xk |
x) 2 |
( yk |
y) 2 |
|
|||
|
|
|
k 1 |
|
k 1 |
|
|
|
|
|
Можно непосредственно вычислять коэффициент по этой формуле, но удобнее выполнять действия по следующему алгоритму (стр. 196-198 или учебное пособие [2] ) .
Полученное при помощи средств EXCEL значение коэффициента корреляции данных массивов равно rxy 0,8328 . Выбираем
функции статистические функции корреляция на панели инструментов.
ШАГ 5. Проверяем гипотезу о статистической значимости выборочного коэффициента корреляции (стр. 265-266)
Выдвигаем основную гипотезу H0 : rxy 0 и соответствующую альтернативную
гипотезу H1 : rxy 0 . На заданном уровне значимости находим теоретическое значение статистики критерия согласно выражению
|
|
t |
|
(n 2) |
||||
Z |
1 |
2 |
|
|
|
|
||
|
|
|
|
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|
n 2 |
(t |
|
(n 2))2 |
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
