
Математика Сам раб 140400 140100
.pdf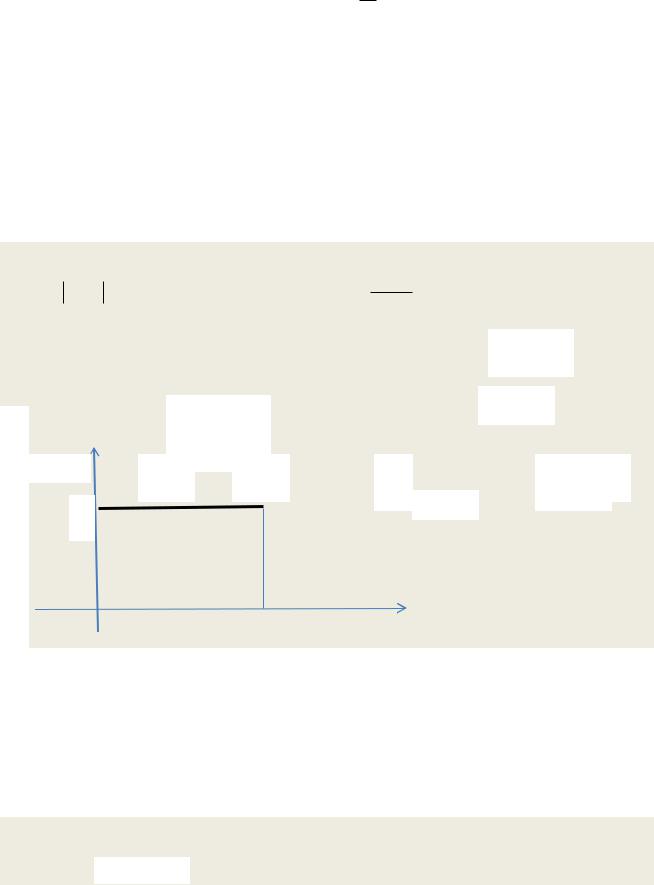
51
1
V ( ) Im S( ) f (t) sin tdt,
0
который называют синус-преобразованием Фурье.
Обратные преобразования задаются следующими соотношениями:
|
|
f (t) U ( ) cos td ; |
f (t) V ( ) sin td . |
0 |
0 |
ЗАДАЧИ
1.Для заданной функции найдите спектральную плотность S( ) , амплитудный
спектр S( ) , фазовый спектр ( ) arctg V ( ) . Постройте графики
U ( )
амплитудного и фазового спектров
1)
E
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
0 |
|
T |
|
|
|
|
|
|
|
2) f (t) exp( |
|
t |
|
) , |
3) f (t) |
|
1 |
|
|
|
|
|
|
|
|||||
|
|
t 4 |
1 , |
||||||
|
|
||||||||
|
4) f (t) (t) |
|
5) cos( 0t) , |
||||||
Ответы:

52
1. 2. S( ) |
E |
sin L i(cos L 1) |
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. S( ) |
1 |
|
|
|
|
|
S( ) |
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
3. |
|
exp |
|
|
sin |
|
|
|
|
|
||||
2 |
2 |
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
2 |
|
2 |
|
|
4 |
|
|||||||
2.Восстановите функцию по заданному спектру:
1)
Для данной задачи определите время перехода f (t) через нуль как функцию ширины спектра. Определите предельный процесс при условии 0 .
2). S( ) |
Ab |
, |
A 0, |
b 0 |
( 2 b 2 ) |
Преобразования Лапласа.
Оригинал и изображения по Лапласу.
Преобразованием Лапласа для функции f (t) называется функция
F( p) f (t)e pt dt L f (t) ,
0
где p i - комплексная переменная. Функция f (t) является комплексной функцией действительного аргумента и называется функциейоригиналом. Эта функция обладает следующими свойствами:
1)f (t) 0 для всех t 0 ;
2)f (t) интегрируема на любом конечном интервале;
|
|
|
|
|
|
53 |
|
|
|
|
|
|
3) f (t) возрастает не |
быстрее |
некоторой |
|
показательной функции, то есть |
||||||||
существуют такие |
M 0 |
и |
0 |
0 , |
|
что |
для |
всех |
t справедливо |
|||
| f (t)| M exp( 0t) . |
|
|
|
|
|
|
|
|
|
|
|
|
Число 0 называют показателем |
роста |
функции |
f (t) . При |
этих условиях |
||||||||
несобственный интеграл сходится абсолютно: |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
f (t)e pt dt |
|
|
. |
|
|
||||
|
|
|
|
|
||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Формула обращения |
|
|
|
|
|
|
|
|
|
|
|
|
Пусть справедливо соотношение: |
|
|
|
|
|
|
|
|
||||
|
|
|
|
f (t) F( p) |
|
|
|
|||||
Если функция-оригинал f (t) непрерывна в точке |
t и имеет в этой точке |
|||||||||||
непрерывные конечные производные, то |
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
F( p)e pt dp. |
|
|
|||||
|
f (t) = 2 i |
|
|
|||||||||
|
i |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, по известному изображению F ( p) оригинал f (t) может быть
восстановлен путем вычисления интеграла обращения. Интеграл обращения может быть вычислен с применением теории вычетов. Поэтому при нахождении оригиналов обычно используют теоремы разложения, которые следуют непосредственно из формулы обращения.
Первая теорема разложения. |
|
|
|
|
|
|
|
|
|
Пусть изображение Лапласа F ( p) |
является функцией, аналитической в |
||||||||
окрестности p , и разложение в ряд Лорана в окрестности |
p имеет |
||||||||
вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F( p) |
Ck |
. |
|
|
|
|
|
||
k |
|
|
|
|
|
||||
|
k 1 p |
|
|
|
|
|
|||
|
|
|
|
|
Ck |
|
|
|
|
Тогда оригиналом является функция |
f (t) (t) , где |
f (t) |
|
|
t k 1 . |
||||
(k |
1)! |
||||||||
|
|
|
|
k 1 |
|
||||

54
Пример 1. Найти функцию-оригинал для функции-изображения:
1
F( p) e p 1.
Восстановим оригинал f (t) (t) . Для этого разложим функциюизображение в ряд Лорана:
|
|
|
|
F ( p) 1 |
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
... |
( 1)k |
... 1 |
||||||||||||
|
|
|
|
|
p |
2! p2 |
|
3! p3 |
k ! pk |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
... |
( 1) k |
|
|
... |
|
|
|||||||
|
|
|
|
|
p |
|
|
2! p2 |
3! p3 |
|
|
k ! pk |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
( 1) |
k |
|
|
|
|
|
|
( |
1) |
k |
|
|
|
|
t |
|
t |
2 |
|
|||||||||
|
C |
|
|
|
, f (t) |
|
|
t k 1 1 |
|
|
... |
|||||||||||||||||||||
Отсюда |
k |
k ! |
|
k !(k 1)! |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
2 |
12 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Сопоставляя это разложение с формулой Маклорена:
f (t) |
f (0) f |
(0)t |
f (0) |
t |
2 ... |
|
||
2! |
, |
|||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
получаем начальное |
значение функции f (0) 1, |
начальную скорость |
||||||
изменения функции f |
|
1/ 2 . |
|
|
|
|
|
|
(0) |
|
|
|
|
|
|||
Вторая теорема разложения
Пусть изображение Лапласа F ( p) является правильной дробью:
F( p) Pn ( p) ; n m.
Qm ( p)
Тогда оригиналом является функция f (t) (t) , где

55
n
f (t) res F( pk )e pk t .
k 1
Сумма вычетов берется по всем особым точкам, лежащим в конечной части комплексной плоскости.
Если изображение F ( p) является неправильной дробью, то необходимо выделить целую часть и при нахождении оригинала использовать свойство линейности.
p 3
Пример 2. F( p) p2 4 p 13 .
Так как дробь правильная, сразу находим особые точки: p 2 3i , которые являются простыми полюсами. Сумму вычетов в комплексно сопряженных точках удобно находить по формуле:
res F ( p)e p t p i |
+ res F ( p)e p t p i = 2Re res F ( p)e p t p i . |
|||||||
|
( p 3)e |
pt |
|
|
( p 3)e |
pt |
|
|
f (t) 2 Re res |
|
|
2 Re res |
|
|
|
||
|
|
|
|
|||||
p2 4 p 13 p 2 3i |
|
2 p 4 |
p 2 3i |
|
||||
|
|
( 2 3i 3)e( 2 3i )t |
(1 3i)e 2t (cos3t i sin 3t) |
|
||||||||
Re |
|
|
|
Re |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 3i 2 |
|
3i |
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
||||
Re |
|
|
|
( i 3)(cos3t i sin 3t)e2t |
e2t cos3t |
|
|
sin 3t |
|
|||
3 |
3 |
|
||||||||||
|
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p2 2
Пример 3. F ( p) = p( p2 4) .
|
( p |
2 |
2)e |
pt |
|
|
( p |
2 |
2)e |
pt |
|
||
f (t) res |
|
|
|
|
2 Re res |
|
|
|
|
||||
p( p2 4) |
|
p( p2 4) |
|||||||||||
|
|
p 0 |
|
|
p 2i |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
56 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( p2 2)e pt |
|
|
|
p 0 |
2 Re |
( p2 2)e pt |
|
|
|
|
|
|
|
1 |
2 Re |
( 4 2)e2it |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
p2 4 |
|
|
|
p( p 2i) |
|
p 2i |
|
2 |
2i(4i) |
|||||||||||||||||||||||||
|
|
|
|
|
1 |
2 Re |
( 4 2)e2it |
|
|
1 |
|
Re |
|
( 2)e2it |
|
|
|
|||||||||||||||||
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
2i(4i) |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|||||||||||
|
|
|
1 |
|
1 |
Re(cos2t i sin 2t) |
1 |
|
|
|
1 |
cos2t. |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 4. F ( p) = |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
p2 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
p2 |
|
|
|
|
|
|
p2 4 4 |
1 |
|
|
4 |
|
|
(t) 2 sin 2t. |
|
|||||||||||||||||
|
|
p2 4 |
|
|
p2 4 |
p2 4 |
|
|||||||||||||||||||||||||||
ТАБЛИЦА: ОСНОВНЫЕ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА И ИХ СВОЙСТВА
f (t) |
|
|
F ( p) |
f (t) |
|
|
|
|
F ( p) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t) |
1 |
|
|
|
|
t neat |
|
|
|
|
n! |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( p a)n 1 |
|||
(t) |
1 |
|
|
|
|
f (t) |
|
|
pF(P) f (0) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
|
|
|
|
f (t) |
p |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
F( p) pf (0) f (0) |
||||||
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ea t |
|
1 |
|
|
|
|
ea t f (t) |
|
|
|
|
F( p a) |
|||||
|
|
|
p a |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 p |
||||||||
sin t |
|
|
|
t sin t |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
( p2 2 )2 |
||||||
|
p2 2 |
|
|
|
|||||||||||||
cos t |
|
|
|
p |
|
t cos t |
|
|
|
|
p2 2 |
||||||
|
p2 2 |
|
|
|
|
|
|||||||||||
|
|
|
|
( p2 2 )2 |
|||||||||||||
|
|
|
|
t sh t |
|
|
|
|
2 p |
||||||||
sh t |
|
|
|
|
|
|
|
|
|||||||||
|
p2 2 |
|
|
|
|
( p2 2 )2 |
|||||||||||
57
ch t |
p |
t ch t |
p2 2 |
p2 2 |
|
||
( p2 2 )2 |
e t sin t |
|
|
|
|
F( p)G( p) |
|||
|
|
|
|
|
|
f ( )g(t ) |
|
|
|
( p )2 2 |
|
||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
p |
f (0)g(t) f ( )g(t )d pG( p)F( p) |
|||||
e t cos t |
( p )2 2 |
|||||||
|
|
|||||||
|
|
|
|
|
|
|
||
|
|
1 |
|
|
f (t ) |
e p F( p) |
||
t |
|
|
p 2 |
|
||||
|
|
|
|
|||||
t n |
|
|
n! |
|
|
|
||
|
|
pn 1 |
|
|
||||
ЗАДАЧИ
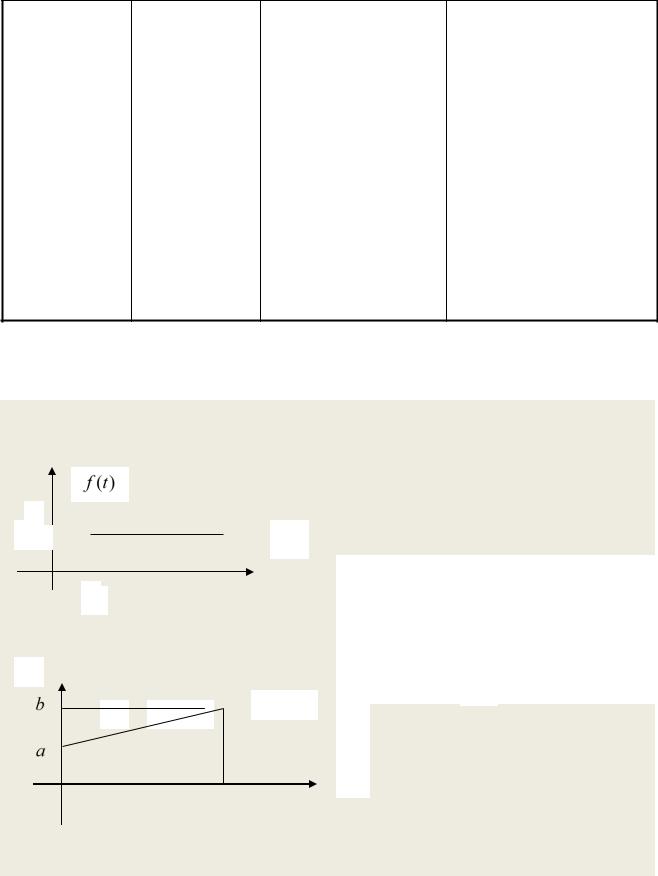
1. Найдите изображение F ( p) по оригиналу f (t) , используя определение преобразований Лапласа.
1)
1
τ
2) 
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
t |
|
|
|
|
|
|
|
|
|
|
Ответы:

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
58 |
|
1. |
F ( p) |
1 e p |
, |
|
|
|
|
|
|
|
|
|
||||||
|
p 2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
b a 1 |
|
a |
b a 1 |
|
b |
|||||||||||
2. F ( p) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e pT |
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
||||||
|
|
|
T |
|
|
p |
|
|
p |
|
T |
|
p |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
p |
||||||
2. Найдите изображение по оригиналу, используя таблицу и свойства преобразований Лапласа.
sin(2t), cos(3t), e4t , tet , t2et , sh( t), ch( t), tch2t,
|
sin2 t, sin4 t, |
e5t sin 2t, |
|
e 5t cos 3t, |
cht cos 2t, |
|||||||||||||||
|
4t |
|
|
|
|
|
t |
|
|
|
|
|
|
2 |
t 2 |
|||||
e |
|
|
(sin 3t cos 2t), |
|
te |
|
sin( t), sin |
|
|
|
|
|
(t 2), |
|||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
e3(t4) (t 4), |
exp(at) exp(bt) |
, |
|
cos at cos bt |
, |
|
|
|||||||||||||
|
|
|
t |
|
|
|
|
|
t |
|
|
|
|
|
||||||
|
cos a cos b d , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
e at sin t , |
|
(t )2 cos 2 d |
|
|
||||||||||||||
|
t |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
t |
|
|
|
|
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
et sin(t )d , |
|
e t sin( t ), |
|
e t |
cos( t ) |
|||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Преобразования Лапласа: восстановите оригинал по изображению
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F ( p) |
|
|
Ответ : f (t) |
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
et sin t |
|
|
||
|
|
p 2 |
2 p 2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
p 8 |
|
|
|
3et 2e 2t |
|
|
|||||
|
|
p 2 |
p 2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
p 1 |
|
|
t 1 cost sin t |
|
|
||||||
|
|
p 2 ( p 2 1) |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
(sin t t cost) |
|
|
|
|
( p2 1)2 |
|
|
2 |
|
|
||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
59 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
p 2 3 p 4 |
|
|
|
|
2 8et |
7e2t |
|
|
|
|
|||||||||||||||||||||||
|
|
p( p 1)( p 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
p 2 1 |
|
|
|
|
|
|
|
t 2 et (2t 2) |
|
|
|||||||||||||||||||||||
|
|
p 2 ( p 1) 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
p 2 6 |
|
|
|
|
5 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2t |
|
|
|
t cos 2t |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
4 |
|
|
|||||||||||||||||
|
|
( p 2 4) 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
p3 p 4 |
|
|
|
|
1 |
(e |
3t |
e |
t |
) e |
t |
(cost sin t) |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
p 4 5 p 2 10 p 6 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
p 2 3 |
|
|
|
|
|
|
(t) 2e t |
cost 3e t sin t |
|
|
|||||||||||||||||||||||
|
|
p 2 2 p 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
e 3 p |
|
|
|
|
|
sin (t 3) (t 3) |
|
|
||||||||||||||||||||||||||
|
|
p 2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
e 5 p |
|
e 2 p |
|
|
|
|
|
|
(t 5) (t 5) e3(t 2) (t 2) |
|
|
|||||||||||||||||||||||
|
|
p 2 |
|
|
p 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t 2 |
|
1 t 4 |
|
|
|
|
||||||||||||
|
|
p |
exp( |
p 2 |
) |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
2 |
2! |
4! |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.Решение линейных дифференциальных уравнений с постоянными
коэффициентами операторным методом
Задача Коши для линейного уравнения:
an y(n) an 1 y(n 1) ... a1 y a0 y x(t)
состоит в нахождении частного решения y(t) по заданным начальным условиям
|
|
, |
|
|
, ...........y0 |
n 1 |
(0) |
n 1 |
y(0) y0 , y (0) |
y0 |
y (0) |
y0 |
|
y0 |
Полагаем, что правая часть уравнения x(t) и искомая функция y(t) являются оригиналами. Тогда для них существует преобразование Лапласа:
x(t) X ( p), y(t) Y( p).
Применяя правило дифференцирования оригинала

60
y (t) pY( p) y(0),
y (t) p2Y( p) py(0) y (0),
y (t) p3Y( p) p2 y(0) py (0) y' ' (0),
................................
и используя свойство линейности, переходим в исходном дифференциальном уравнении от оригиналов к изображениям. При этом исходное дифференциальное уравнение переходит в алгебраическое уравнение
относительно Y ( p) :
an ( pnY( p) pn 1 y0 ... y0(n 1) ) ... a0Y( p) X ( p).
Тогда
Y( p)(an pn an 1 pn 1 ... a0 ) X ( p) M( p),
Y( p) K( p) X ( p) M( p);
K( p) an pn an 1 pn 1 ...a1 p a0 ;
Y( p) X ( p) M ( p) .
B этом выражении стоящий в знаменателе многочлен K ( p) называется
характеристическим многочленом, а функция K ( p) выражает влияние
начальных условий.
Решение исходного дифференциального уравнения получаем, возвращаясь к оригиналам Y ( p) y(t) .
Пример 5. Найти частное решение уравнения
y 2y 5y 3, y(o) 1; y (0) 0.
