
Математика Сам раб 140400 140100
.pdf
91
Выбрав уровень значимости 0,1, находим по таблице (стр. 414) квантиль
распределения Стьюдента |
|
t |
(n 2) t0,95(3) 2,353 |
и вычисляем значение |
||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
статистики |
Z |
|
|
2,353 |
|
0,81. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
||||
|
(2,353)2 |
|
||||||
|
3 |
|
|
|
|
|||
Основная гипотеза принимается, если выполняется соотношение rxy Z и отвергается в случае rxy Z .
В рассматриваемом случае rxy Z . Поэтому основная гипотеза отклоняется и принимается гипотеза H1 : rxy 0 . Таким образом, коэффициент корреляции на
выбранном уровне значимости отличен от нуля. Это свидетельствует о наличии корреляционной зависимости между случайными величинами. Значение коэффициента корреляции близко к единице , что говорит о близости зависимости между случайными величинами к линейной зависимости.
2. НАХОЖДЕНИЕ ПАРАМЕТРОВ УРАВНЕНИЯ ЛИНЕЙНОЙ РЕГРЕССИИ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
( стр. 291298 )
Пусть коэффициент корреляции между двумя случайными величинами значимо отличается от нуля и близок к единице. Предполагаем ( выдвигаем гипотезу ) , что эти случайные величины связаны « в среднем» линейной зависимостью :
Y AX B X A1Y B1
РЕГРЕССИЯ – оптимальная зависимость, то есть модель, обеспечивающая аппроксимацию эмпирических данных с наибольшей точностью. Справедливо соотношение
|
Y AX B |
Коэффициенты A, B, A1 , B1 являются параметрами линейной регрессионной модели. |
|
Величина |
- случайная ошибка наблюдений, причем математическое ожидание |
M 0, |
D 2 |
Для нахождения оценок параметров модели используем метод наименьших квадратов. Согласно этому методу в качестве оценок параметров выбирают такие, которые обеспечивают минимум суммы квадратов отклонений наблюдаемых значений

92
случайных величин от их математических ожиданий. Другими словами параметры должны быть такими, чтобы сумма
~ ~ |
n |
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|||
S( A, B) yk ( Axk B) 2 |
принимала наименьшее значение. Записываем |
|
||||||
|
k 1 |
|
|
|
|
|
~ |
~ |
|
|
|
|
|
|
|
||
необходимые условия существования экстремума для функции двух переменных A, B , |
||||||||
приравнивая к нулю частные производные |
|
|
|
|||||
|
|
|
S |
n |
~ |
~ |
|
|
|
|
|
|
|
||||
|
|
|
~ 2 yk ( Axk |
B) xk 0 |
|
|||
|
|
|
A |
k 1 |
|
|
|
|
|
|
|
S |
n |
|
~ |
|
|
|
|
|
~ |
2 yk ( Axk B) 0 |
|
|||
|
|
|
B |
k 1 |
|
|
|
|
В результате для нахождения оценок получаем систему уравнений:
|
|
|
|
|
|
|
|
|
|
~ n |
2 |
|
|
|
~ n |
n |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
A xk |
B xk xk yk |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
k 1 |
k 1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
~ n |
|
|
~ |
|
n |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
A xk |
Bn yk |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
Решение системы имеет вид : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
n |
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
~ |
n xk yk |
xk yk |
Qxy |
|
|
|
|
~ |
|
yk |
~ |
xk |
~ |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
k 1 |
||||||
|
|
|
|
A |
|
k 1 |
k 1 |
k 1 |
|
|
|
|
|
, |
|
|
B |
|
A |
y Ax . |
||||
|
|
|
|
|
n |
n |
|
|
Qx |
|
n |
n |
||||||||||||
|
|
|
|
|
|
2 |
( xk ) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
n xk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
k 1 |
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично находим оценки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
~ |
Qxy |
|
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A1 |
|
, |
B1 |
x A1 y |
. При этом |
|
|
AA1 |
rxy |
. |
|
|
|
|
|
|
||||||||
Qy |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для рассмотренной задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
xk |
|
|
yk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,9 |
|
|
6,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,7 |
|
|
12,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,3 |
|
|
11,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4,6 |
|
|
15,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5,3 |
|
|
14,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
93
|
|
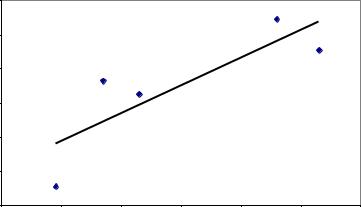
Корреляционная диаграмма |
|
|
|
|
17 |
|
|
|
|
|
|
15 |
y = 1,6225x + 7,1774 |
|
|
|
|
|
|
|
R2 = 0,6937 |
|
|
|
|
13 |
|
|
|
|
|
|
Y |
|
|
|
|
|
|
11 |
|
|
|
|
|
|
9 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
X |
|
|
|
имеем оценки
A 1,62 |
B 7,18 |
A1 0,44 |
B1 2,26 |
|
И уравнения регрессии имеют вид |
Y 1,62X 7,18 |
|||
|
|
|
|
X 0,44Y 2,26 |
Достаточно легко написать программу для получения оценок по методу наименьших квадратов как для линейной , так и для других зависимостей. Но существует много готовых программных средств, решающих эту задачу. Так средства EXCEL
позволяют непосредственно получить уравнение линейной регрессии по рядам данных:
Мастер диаграмм точечная диаграмма линия тренда(правая кнопка мыши выводится на точку)
|
|
|
|
94 |
|
|
Регрессионная модель называется адекватной, если предсказанные по ней |
||||||
значения переменной Y согласуются с результатами наблюдений. Оценка |
||||||
адекватности может быть проведена следующим образом. |
|
|||||
Непосредственный анализ остатков, то есть разностей между |
||||||
наблюдаемыми значениями yk |
и вычисленными согласно уравнению |
|||||
|
~ |
~ |
~ |
|
|
|
регрессии Yk |
Axk |
B : |
|
|
|
|
k yk |
~ |
|
|
|
|
|
Yk . |
|
|
|
|
|
|
Если модель адекватна, то остатки, которые являются реализациями случайных |
||||||
ошибок наблюдений, должны быть нормально распределенными случайными |
||||||
величинами с нулевым средним и одинаковыми дисперсиями 2 . Другими |
||||||
словами для случайной величины - остатков – необходимо выполнить |
||||||
лабораторную работу № 1(найти среднее, дисперсию, среднеквадратичное |
||||||
отклонение) и доказать, что на заданном уровне значимости 0 (нулевое |
||||||
значение попадает в доверительный интервал для математического |
||||||
ожидания). |
|
|
|
|
|
|
Пример построения прямой регрессии в Excel. |
|
|
||||
|
|
|
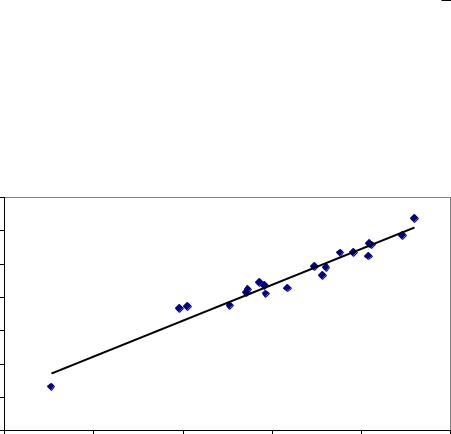
Корреляционная диаграмма |
|
|
|
14 |
|
|
|
|
|
|
12 |
y = 2,162x - 0,9681 |
|
|
|
||
|
R2 = 0,9548 |
|
|
|
|
|
10 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
Y |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
1,5 |
2,5 |
3,5 |
4,5 |
5,5 |
6,5 |
|
|
|
|
|
X |
|
|
95
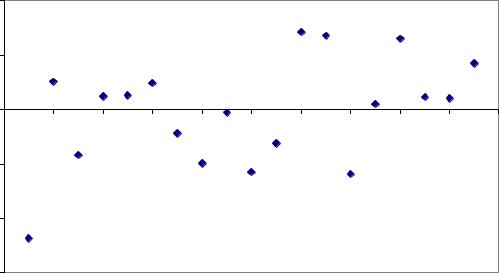
График остатков
1
0,5
0
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
-0,5
-1
-1,5
Данные описательной статистики для случайной величины “остатки”
Среднее |
6,66134E-16 |
Стандартная ошибка |
0,108822029 |
Медиана |
0,109108445 |
Мода |
|
Стандартное отклонение |
0,486666907 |
Дисперсия выборки |
0,236844679 |
Эксцесс |
0,294111648 |
Асимметричность |
-0,602186657 |
Интервал |
1,892506228 |
Минимум |
-1,181791019 |
Максимум |
0,710715209 |
Сумма |
1,33227E-14 |
Счет |
20 |
Уровень |
0,227767194 |
надежности(95,0%) |
|
Из приведенных зависимостей и расчетов видно, что предложенная регрессионная модель адекватна: остатки распределены около нулевого среднего. Значение стандартной ошибки 0,1088 задает доверительный интервал для M , содержащий значение 0 .
Статистическую значимость регрессионной модели можно проверить по коэффициенту регрессиии A .

96
Линейная регрессионная модель называется незначимой, если параметр A 0 . Проверку основной гипотезы H0 : A 0 против альтернативной гипотезы
H1 : A 0 можно провести двумя способами.
СПОСОБ 2 . Находим границы доверительного интервала для параметра A :
|
S t |
(n 2) |
|
|
|
S t |
(n 2) |
|||||
~ |
1 |
2 |
|
|
|
|
~ |
1 |
2 |
|
||
A |
|
|
|
|
|
|
A |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Q |
x |
|
|
Qx |
||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
Если для данного уровня значимости доверительный интервал содержит значение A 0 , то принимается основная гипотеза и регрессия считается статистически незначимой. В том случае, когда доверительный интервал не содержит нулевое значение параметра, основная гипотеза отклоняется и регрессионная модель считается статистически значимой
Например : 0,12 A 3.08 или |
P(0,12 A 3,08) 0,9 . |
Таким образом, на заданном уровне значимости нулевое значение параметра не попадает в доверительный интервал и регрессия признается статистически значимой
Полезной и важной характеристикой линейной регрессии является коэффициент детерминации R2 , который вычисляют по формуле
|
n |
~ |
~ |
2 |
|
|
|
|
|||
|
(( Axk B) y) |
|
|
||
R2 |
k 1 |
|
|
|
. |
|
n |
|
|
||
|
|
( yk y)2 |
|
|
|
k 1
Этот коэффициент показывает долю разброса результатов наблюдений около
средего значения случайной величины y , которую можно объяснить построенной регрессионной моделью , и может быть использован для характеристики не только линейной регрессии, но и для нелинейной. Как видно из определения коэффициента, чем меньше остаточная сумма квадратов Qe , тем ближе значение коэффициента к единице и тем точнее выбранная модель
регрессии описывает результаты наблюдений. Значение корня R является оценкой коэффициента корреляции между результатами наблюдений и их значениями, вычисленными согласно принятой регрессионной модели. В случае
линейной регресссии справедливо rxy R . Отметим, что именно значение
97
коэффициента детерминации указывается в EXCEL в качестве характеристики качества аппроксимации.
Ниже приведена выдача из Excel: Сервис Анализ данных Регрессия , для
подробного анализа которой следует обратиться к книге [3]. Отметим только, что красным цветом выделен 95% доверительный интервал для коэффициента
регрессии A : P 1,736 A 2,358 0,95.
ВЫВОД ИТОГОВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная |
|
|
|
|
|
|
статистика |
|
|
|
|
|
|
Множес |
0,95603 |
|
|
|
|
|
твенный |
7 |
|
|
|
|
|
R |
|
|
|
|
|
|
R- |
0,91400 |
|
|
|
|
|
квадрат |
6 |
|
|
|
|
|
Нормир |
0,90922 |
|
|
|
|
|
ованны |
9 |
|
|
|
|
|
й R- |
|
|
|
|
|
|
квадрат |
|
|
|
|
|
|
Станда |
0,50000 |
|
|
|
|
|
ртная |
3 |
|
|
|
|
|
ошибка |
|
|
|
|
|
|
Наблюд |
20 |
|
|
|
|
|
ения |
|
|
|
|
|
|
Дисперсионный анализ |
|
|
|
|
||
|
df |
SS |
MS |
F |
Значимост |
|
|
|
|
|
|
ь F |
|
Регресс |
1 |
47,83 |
47,83 191,3179 |
4,96562E- |
|
|
ия |
|
|
|
|
11 |
|
Остаток |
18 |
4,50004 |
0,25000 |
|
|
|
|
|
9 |
3 |
|
|
|
Итого |
19 |
52,3300 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
Коэффи Станда |
t- |
P- |
Нижние |
Верхние 95% |
|
|
циенты |
ртная |
статис Значени |
95% |
|
|
|
|
ошибка |
тика |
е |
|
|
Y- |
-0,43605 |
0,71897 -0,60648 0,551766 |
- |
1,074464255 |
||
пересеч |
|
5 |
|
4 1,94655767 |
|
|
ение |
|
|
|
|
9 |
|
Переме |
2,04779 |
0,14805 |
13,8317 |
4,966E- 1,73675383 |
2,358837984 |
|
нная X |
6 |
|
7 |
11 |
6 |
|
1 |
|
|
|
|
|
|
98
Тестовые задачи
1.Вероятность того, что при бросании игрального кубика выпадет 0 очков , составляет …
2.В урне находится 5 белых и 2 черных шара. Из урны вынимаются четыре шара. Вероятность того, что 2 шара будут белыми, а 2 черными, равна …
3.В урне находится 5 белых и 3 черных шара. Из урны вынимаются четыре шара. Вероятность того, что два шара будут белыми, а два – черными, равна …
4.В урне находится 5 белых и 5 черных шаров. Из урны вынимаются четыре шара. Вероятность того, что все шары будут белыми, равна …
5.Игральная кость бросается один раз. Тогда вероятность того, что на верхней грани выпадет не менее четырех очков, равна…
6.По мишени производится четыре выстрела. Значение вероятности промаха при первом выстреле 0,4; при втором - 0,3; при третьем – 0,2; при четвертом – 0,1. Тогда вероятность того, что мишень не будет поражена ни разу равна…
7.По мишени производится четыре выстрела.
Значение вероятности промаха при первом выстреле 0,6; при втором – 0,5; при третьем – 0,4; при четвертом – 0,3.
Тогда вероятность того, что мишень будет поражена все четыре раза, равна…
8.В урне лежит 3 белых и 3 черных шара. Последовательно, без возвращения и наудачу извлекают 3 шара. Тогда вероятность того, что первый и третий шар будут черными, а второй белым, равна …
9.Вероятность того, что студент сдаст экзамен, равна 0,8. Тогда вероятность того, что студент сдаст хотя бы один из 3 экзаменов сессии, равна …
10.При бросании точки достоверно ее попадание на отрезок длины D; попадание в
любую точку отрезка равновероятно. Вероятность 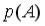 ее попадания на отрезок длины d равна…
ее попадания на отрезок длины d равна…
100
17.Статистическое распределение выборки имеет вид
Тогда относительная частота варианты 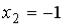 , равна …
, равна …
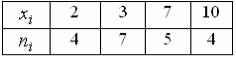
18.Из генеральной совокупности извлечена выборка объема n=50:
Тогда n4 равен…
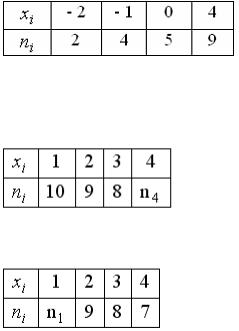
19.Из генеральной совокупности извлечена выборка объема n=50:
Тогда n1 равен…
20.Мода вариационного ряда 2 , 5 , 5 , 6 , 7 , 9 , 10 равна …
21.Дана выборка объема n. Если каждый элемент выборки увеличить на 5 единиц, то выборочное среднее 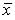 …
…
22.Дана выборка объема n. Если каждый элемент выборки увеличить в 4 раза, то выборочное среднее 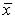 …
…
23.Дана выборка объема n. Если каждый элемент выборки уменьшить на 8 единиц, то выборочное среднее 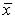 …
…
24.Проведено 5 измерений (без систематических ошибок) некоторой случайной величины (в мм): 5, 6, 9, 10, 11. Тогда несмещенная оценка математического ожидания равна…
25.Проведено 5 измерений (без систематических ошибок) некоторой случайной величины (в мм): 9, 10, 13, 14, 15. Тогда несмещенная оценка математического ожидания равна…
26.Случайная величина распределена равномерно на интервале 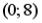 . Тогда ее математическое ожидание и дисперсия соответственно равны …
. Тогда ее математическое ожидание и дисперсия соответственно равны …

 и
и  , образующих полную группу событий. Известны
, образующих полную группу событий. Известны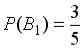 и условные вероятности
и условные вероятности 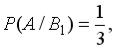
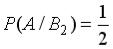 .
.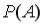 равна …
равна …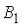 и
и 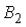 , образующих полную группу событий. Известны
, образующих полную группу событий. Известны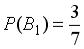 и условные вероятности
и условные вероятности 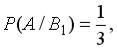
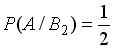 .
.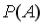 равна …
равна …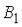 и
и 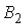 , образующих полную группу событий. Известны
, образующих полную группу событий. Известны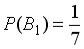 и условные вероятности
и условные вероятности 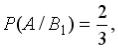
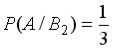 .
.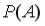 равна …
равна …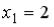 , равна …
, равна …