1. Получение дискретных передаточных функций

Дискретные передаточные функции получаются как на основе непрерывных передаточных функций, так и на основе разностных уравнений. Наибольший интерес представляет первый случай, который символически записывается так:

. (10)

При получении W(z) на основеW(p) наибольшее распространение получили два метода:

• табличный метод;

• метод подстановки.

При табличном методе исходными данными для получения W(z) являются либо непрерывные передаточные функцииW(p), либо весовые функции(t). Далее по таблице, приведенной в приложении А, определяется дискретная передаточная функцияW(z). Единственная проблема, которая здесь имеет место, состоит в том, что в таблице приведеныZ-изображения только для передаточных функций невысокого порядка. ЕслиW(p) является передаточной функцией высокого порядка, то ее необходимо предварительно разложить в сумму дробно-рациональных членов, каждый из которых представлен в таблице А.1. Подробно методы разложения рассмотрены в [5].

При методе подстановок осуществляется приближенный переход от W(p) кW(z). В настоящее время известны два вида подстановок:

• общая подстановка, полученная при выполнении операций численного интегрирования по методу прямоугольников

; (11)

• подстановка Тастина, полученная Тастиным при выполнении операций численного интегрирования по методу трапеций

. (12)

При получении дискретной передаточной функции W(z) на основе разностных уравнений исходными являются уравнения вида (1), которые записываются в операторной форме, то есть в виде

. (13)

Вынесем за скобки Y(z) иV(z):

. (14)

Откуда имеем, что

. (15)

2. Получение разностных уравнений.

В работе разностные уравнения получаются на основе:

• дифференциальных уравнений;

• интегро-дифференциальных уравнений;

• дискретных передаточных функций.

В качестве исходных рассматриваются дифференциальные уравнения вида:

, (16)

где k– коэффициент передачи;

T₁, …,T_n,t₁, …,t_m– постоянные времени.

Для получения разностных уравнений в выражении (16) дифференциалы заменяются приближенно левыми разностями:

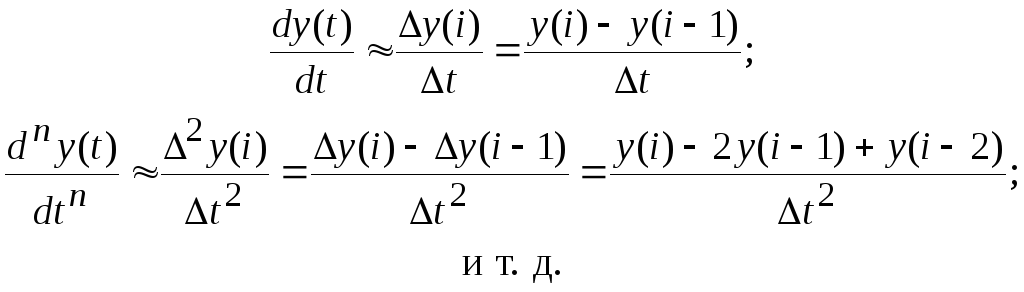(17)

где Dy(i),D²y(i) – разности первого и второго порядков.

После замены дифференциалов разностями приводятся подобные члены, в результате чего получается итоговое разностное уравнение. При получении разностных уравнений на основе дифференциальных порядок разностного уравнения всегда совпадает с порядком дифференциального уравнения.

При получении разностного уравнения для интегро-дифференциального уравнения необходимо учитывать особенность получения разностного уравнения для операции интегрирования, то есть для интеграла вида:

. (18)

При численном интегрировании по методу прямоугольников интеграл (18) заменяется суммой

. (19)

Так как (см. рисунок 2) интеграл (18) представляет собой площадь криволинейной трапеции, то сумма (19) представляет собой площадь прямоугольников с основаниями равными Dtи высотойv(i). Запишем сумму вида (19) для предыдущего момента времени, то есть

. (20)

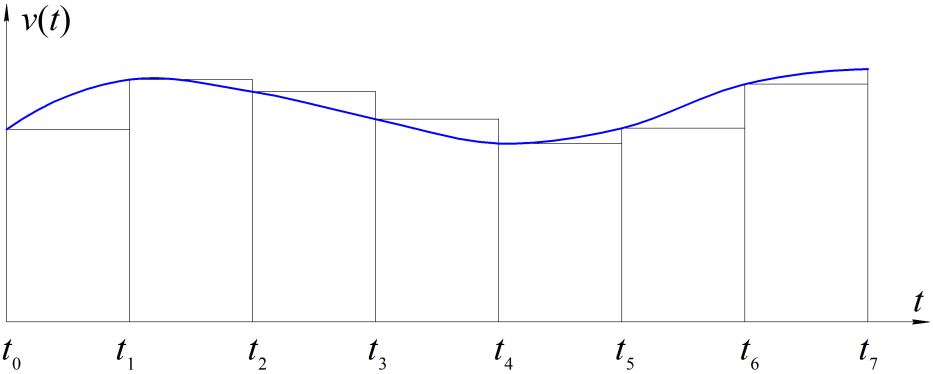
Рисунок 2 – График решетчатой функции

При вычитании суммы (20) из суммы (19) получаем уравнение вида:

. (21)

В итоге разностное уравнение имеет вид:

, (22)

где b₁=kDt.

Методика получения разностных уравнений для интегро-дифференциальных уравнений состоит в следующем:

1. Дифференциалы заменяются левыми разностями на основе формулы (17).

2. Интегралы заменяются суммами вида (19).

3. Полученное уравнение записывается для моментов времени iиi – 1.

4. Уравнение для (i – 1)-го момента времени вычитается из уравнения дляi-го момента времени. После преобразования и приведения подобных членов получается требуемое разностное уравнение.

Разностное уравнение на основе дискретной передаточной функции вида (9) получается следующим образом:

1. Z-изображение выходной переменной записывается в виде:

или

. (23)

2. Левая и правая части уравнения (23) умножаются на знаменатель в правой части. В итоге получается операторное уравнение вида:

. (24)

3. Раскрывая скобки в (24), получается операторное уравнение вида:

. (25)

4. Перейдя во временную область, имеем разностное уравнение вида:

. (26)