Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4605 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Кузбасский государственный технический университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

2 семестр - Математика 2-ая контрольная

.pdf
Скачиваний:
18
Добавлен:
10.05.2015
Размер:
676.98 Кб
Скачать
☆

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Кузбасский государственный технический университет имени Т.Ф.Горбачева

И. А. Ермакова, Гоголин В.А.

МАТЕМАТИКА

Методические указания к контрольной работе №2 для студентов направления подготовки

бакалавров 280700.62 «Техносферная безопасность» профили 280702.62 «Безопасность технологических процессов

и производств» 280705.62 «Инженерная защита окружающей среды»

заочной формы обучения

Рекомендованы учебно-методической комиссией направления 280700.62

вкачестве электронного издания для самостоятельной работы

Кемерово 2014

1

Рецензент

Волков В. М. – доцент кафедры математики

Ермакова Инна Алексеевна, Гоголин Вячеслав Анатольевич. Математика: методические указания к контрольной работе №2 для студентов направления подготовки бакалавров 280700.62 «Техносферная безопасность», профили 280702.62 «Безопасность технологических процессов и производств», 280705.62 «Инженерная защита окружающей среды», заочной формы обучения. [Электронный ресурс] / И. А. Ермакова, В. А. Гоголин. – Электрон. дан. – Кемерово: КузГТУ, 2014. – Систем. требования: любой компьютер, поддерживающий Microsoft Windows –97 и выше, мышь. – Загл. с экрана.

Приводятся задания и методические указания по их решению по темам, которые, согласно рабочей программе, изучаются во 3 семестре. Выполнение заданий, изложенных в методических указаниях, позволяет студенту качественно подготовиться к экзамену, вопросы к которому прилагаются.

© КузГТУ, 2014 © Ермакова И. А., © Гоголин В. А., 2014

2

Дисциплина «Математика» изучается в течение двух семестров: на 1-м курсе во втором семестре и на 2-м курсе в третьем семестре. В третьем семестре 2-го курса студенты заочной формы обучения выполняют контрольную работу №2.

Студент выполняет контрольную работу, выбирая вариант задания по последней цифре зачетной книжки. Если последняя цифра равна 0, то студент решает вариант №10. Работа, выполненная не по своему варианту, не проверяется.

Работу следует выполнять в рукописном виде.

Решения задач должны иметь объяснения в соответствии с методическими указаниями. При отсутствии письменных объяснений, студент должен быть готов дать устные пояснения к решению задач.

ПРОГРАММА 3 СЕМЕСТРА

РАЗДЕЛ 6. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

6.1. Первообразная, неопределенный интеграл и его свойства. Таблица интегралов. Методы интегрирования: подведение под знак дифференциала, замена переменной, интегрирование по частям.

6.2.Определенный интеграл, его свойства и вычисление. Замена переменной под знаком определенного интеграла. Интегрирование по частям. Геометрические приложения определенного интеграла.

РАЗДЕЛ 7. ДИФФЕРЕНЦИАЛНЫЕ УРАВНЕНИЯ

7.1.Дифференциальные уравнения 1 порядка. Общее решение дифференциального уравнения. Задача Коши. Уравнения с разделяющимися переменными. Однородные, линейные уравнения..

7.2.Дифференциальные уравнения порядка выше первого. Случаи понижения порядка. Линейные дифференциальные уравнения с постоянными коэффициентами..

РАЗДЕЛ 8. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

8.1. Пространство элементарных событий. Алгебра событий. Классическое и геометрическое определение вероятности. Комбинаторика.

3

8.2.Вероятность суммы и произведения событий. Условная вероятность. Формулы полной вероятности и Байеса. Повторные независимые испытания. Формулы Бернулли, Пуассона, МуавраЛапласа.

8.3.Дискретные случайные величины. Ряд и функция распределения. Математическое ожидание и дисперсия дискретной случайной величины.

8.4.Непрерывные случайные величины. Функция распределения, плотность распределения, их свойства. Математическое ожидание и дисперсия непрерывной случайной величины. Нормальное распределение.

РАЗДЕЛ 9. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

9.1.Генеральная совокупность и выборка. Точечная оценка параметров распределения случайных величин. Гистограмма, полигон частот, мода, медиана, размах выборки.

9.2.Интервальная оценка параметров распределения случайных величин. Доверительный интервал и доверительная вероятность. Доверительный интервал для среднего и дисперсии нормальной генеральной совокупности.

9.3.Проверка статистических гипотез. Уровень значимости, критическая область, статистические критерии для проверки гипотез о параметрах генеральной совокупности.

9.4.Парная линейная регрессия. Коэффициент корреляции, его свойства, проверка значимости.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ №2

ЗАДАЧА 1. Найти неопределенные интегралы.

Следует запомнить основные интегралы и их свойства:

1. dx x C.

 

6. еxdx ex C

 

xndx

x

n 1

C,( n 1)

7.

 

dx

 

 

tgx C.

2.

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

n 1

cos

 

 

 

 

 

 

 

 

x

3.

 

dx

ln

 

x

 

C

8.

 

dx

 

 

ctgx C.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

sin2 x

 

 

 

 

 

 

 

 

 

 

 

 

 

4

4.

sin xdx cos ax C.

9.

 

 

dx

 

arctgx C.

 

 

 

x2

1

 

 

 

 

 

 

 

 

 

5.

cos xdx sin ax C.

10.

 

 

dx

 

 

arcsin x

C.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 x2

 

Постоянный множитель можно выносить за знак интеграла:

kf ( x )dx k f ( x )dx.

Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций:

( f1 f2 )dx f1dx f2dx.

Рассмотрим применение формулы №2 таблицы интегралов.

Пример 1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x2dx

x2 1

 

C

x3

C

 

 

 

 

 

 

 

 

 

 

 

 

 

2 1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример 2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

dx x 2dx

x 2 1

C

x 1

 

C

1

C

 

x2

2 1

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

Пример 3.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

x1 3 1

 

C

x4 3

C

3x4 3

C

 

 

xdx x1 3dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 3 1

 

 

4 3

 

 

4

 

 

 

Пример 4.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

dx x

2 5dx

x 2 5 1

 

C

x3 5

C

5x3 5

C

5

 

 

 

 

2 5 1

 

 

 

 

 

 

 

x

2

 

 

 

 

 

 

 

 

 

 

 

 

3 5

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рассмотрим применение основных свойств интегралов.

Пример 5.

2xdx 2 x1dx 2 x1 1 C 2 x2 C x2 C

1 1 2

Пример 6.

cos x tgx dx cos xdx 1x dx C sin x ln x C

Пример 7.

5x 4 3x2 1 dx 5 x 4 dx 3 x2 dx dx x5 x3 x C

5

Пример 8.

 

 

 

 

 

3

 

 

dx

6x3

 

 

 

 

2

 

 

 

 

 

 

x

 

 

 

6 x3dx 3 x 1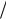2dx 2 dx 6 x4 3 2x1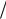2 2x C

4

Рассмотрим применение формулы f kx b 1kF kx b C .

Другими словами, если в подынтегральной функции x умно-

жен на число k, то перед интегралом следует писать множитель 1k .

Пример 9.

sin 5x dx 15 cos 5x C

Пример 10.

 

 

 

 

 

 

 

 

 

 

1

dx

1

 

 

 

2x 1

 

C

 

 

 

 

 

 

 

 

 

ln

 

 

2x 1

2

 

 

 

 

 

 

 

 

 

 

 

Пример 11.

 

 

 

 

 

 

 

 

 

 

3x 2 4 dx

1

 

 

3x 2 5

C

 

 

 

 

 

 

 

3

5

 

 

 

 

 

 

 

Важным способом интегрирования является подведение под знак дифференциала.

Дифференциал функции одной переменной u равен произведе-

нию ее производной на dx, то есть: du u dx .

 

 

Например, u x2 ,

du 2x dx .

 

 

 

Вид интеграла не изменится, если вместо x и

dx в нем

будут

присутствовать функция u f x и du , то есть: f u du F

u C .

Пример 12.

 

 

 

 

 

sin5 x cos x dx

u sin x

 

 

 

du cos x dx

 

 

 

 

 

 

 

 

u5du

u6

C

sin6 x

C

 

 

 

 

 

 

 

 

6

 

6

 

 

 

 

Пример 13.

 

 

 

 

6

 

 

 

 

 

x sin x2 1 dx

u x2 1

 

1

sin u du

1

cos u

du 2xdx

2

2

 

 

cos x2

1 C .

 

 

 

 

1

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ЗАДАЧА 2. Найти площадь фигуры, ограниченной линиями. Для решения этой задачи следует использовать определенный

интеграл, вычисление которого производится по формуле:

 

 

 

 

 

 

 

b

f x dx F( x )

 

b

F b F a .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

 

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рассмотрим применение этой формулы.

Пример 1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

3

 

2

 

 

3

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x2dx

x

 

 

 

 

 

2

 

 

 

1

 

7

2,3.

 

 

 

 

 

 

 

 

 

 

 

 

1

3

 

 

1

 

3

3

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Здесь вместо x подставляем сначала верхнюю границу x 2 , затем нижнюю границу x 1, между выражениями ставим знак «минус».

Пример 2.

3

 

 

 

 

3

3

3

3

4x 3 dx 4xdx

3dx 4 xdx 3 dx

1

1

1

1

1

4

x2

 

 

3

3x

 

31 2 32 2 1 2 3 3 3 1 16 12 4 .

 

 

 

 

 

2

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Пример 3. Найти площадь фигуры, ограниченной линиями: y 2x , y 3 x2 .

Площадь фигуры, расположенной между двумя линиями находится по формуле:

b

S yв yн dx , a

где yв и yн – уравнения соответственно верхней и нижней линий, ограничивающих фигуру; а и b – точки пересечения линий.

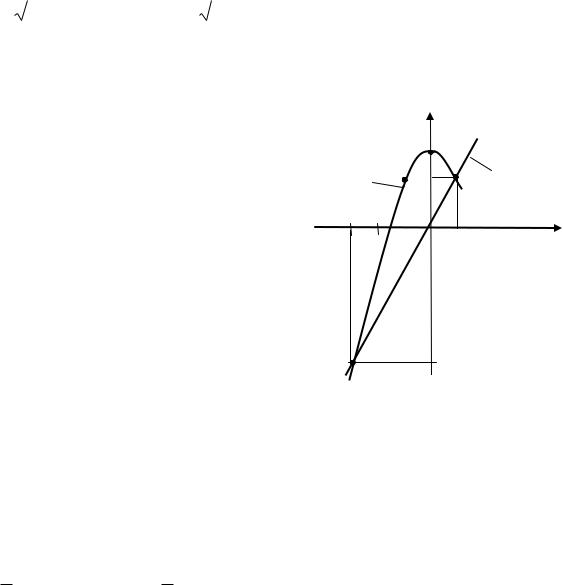
7

Найдем точки пересечения этих линий, для чего приравняем правые части уравнений:

2x 3 x2 x2 2x 3 0 .

 

 

 

Найдем

 

 

дискриминант и

корни:

 

 

D 22 4 3 16 ,

x 2

16

3, x

2

2

16

1.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

2

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Построим линии между точками пересечения, для чего зада-

дим несколько значений x

и найдем соответствующие y.

 

 

 

 

1)

y 2x , это прямая, постро-

 

 

 

 

 

 

 

 

 

 

 

y

 

им ее по двум точкам.

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

-3

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

yн

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

-6

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

в

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y 3 x2 ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2)

 

это парабола,

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

возьмем несколько точек.

 

 

 

–3

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

x

 

-3

 

-1

 

0

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

-6

 

2

 

3

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Из рисунка видим, что

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

yв 3 x2 , yн 2x .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

–6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Найдем площадь:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

b

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

x

3

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

S y

 

 

y

 

dx

3 x2 2x dx 3x

 

 

x2

 

 

 

 

 

 

 

 

в

н

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3 1

1

12

 

 

3

3 3

3 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3

 

 

 

 

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 23 9 9 9 1 23 9 10,7 ед.кв.

ЗАДАЧА 3. Решить дифференциальные уравнения. Дифференциальным уравнением (ДУ) 1-го порядка называется

уравнение, содержащее первую производную y неизвестной функции y f x , которую надо найти. Основным видом ДУ 1 порядка являются уравнения с разделяющимися переменными, которые имеют вид: y x y . Алгоритм решения этих уравнений выглядит следующим образом:

8

1)записывается, что y dydx ;

2)выражения с x переносятся в одну сторону, с y – в другую, то есть разделяются;

3)интегрируются обе части равенства.

Пример 1.

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dy

 

 

 

y

 

 

dy

 

y

 

dx

 

dy

 

 

1

dx .

dx

 

x

 

x

 

 

 

 

x

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

Переменные разделены, интегрируем обе части:

 

dy

 

 

 

1

dx ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

y

 

 

 

 

 

 

dy

 

 

 

1 2 dy

y 1 2 1

2 y1 2

 

 

 

 

y

2

y

,

 

 

 

 

1 2 1

 

y

 

 

 

 

 

 

 

 

 

 

 

 

1x dx ln x C ,

приравниваем полученные выражения и получаем ответ: 2 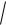y ln x C

Пример 2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

ln x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 y 1 5 x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dy

 

ln x

 

 

 

 

 

dy

ln x

 

dx

2 y 1 5 dy

ln x

dx

 

 

 

 

 

 

 

 

 

dx

x 2 y 1 5

 

 

x 2 y 1 5

x

Переменные разделены, интегрируем:

 

 

 

 

 

2 y 1 5dy

ln x

 

d x .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

2 y 1 5dy

1

2 y 1 6 ,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

6

 

 

 

 

 

 

 

 

 

 

ln x

 

 

u ln x

 

 

u2

ln2 x

 

 

 

 

 

 

 

d x

du

1

 

dx u du

 

 

C

 

C .

 

 

 

x

 

 

 

2

2

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

9

Ответ: 1 2 y 1 6 ln2 x C . 2 6 2

Дифференциальным уравнением (ДУ) 2-го порядка называется уравнение, содержащее вторую производную y неизвестной функции y f x , которую надо найти.

Рассмотрим решение уравнений y f x , допускающих понижение порядка. Путем интегрирования, последовательно находятся первая производная y , а затем функция y .

Пример 3. y sin5x ,

y sin 5x dx

1

cos5x C1,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

1

 

 

 

 

 

1

 

1

 

 

y

 

 

 

 

 

 

cos 5x C

dx

 

 

 

cos 5x dx C

 

dx

 

 

 

 

 

sin x C x C

 

 

 

 

 

 

5

 

 

 

 

 

 

 

 

 

5

 

1

 

 

 

1

 

5 5

1

2

ЗАДАЧА 4. Найти вероятности событий, используя классическое определение вероятности и формулы комбинаторики.

По классической формуле вероятность события А:

P( A ) m A , n

где

n – общее число исходов в испытании, а m – число исходов,

благоприятных для появления события А.

 

 

 

 

Пример 1.

 

 

 

 

Экзамен по математике сдавали 20 студентов, из них сдали 15

человек. Найти вероятности событий: а) студент

сдал экзамен;

б) студент не сдал экзамен.

 

 

 

 

а) Обозначим: событие А – студент сдал экзамен. Общее число

исходов n 20 , число благоприятных исходов m A 15 . Тогда ве-

роятность того, что студент сдал экзамен P( A )

m A

 

15

0,75.

 

 

 

 

 

 

 

 

 

 

n

20

 

 

б) Событие «студент не сдал экзамен» обозначим – А (не А).

 

Общее число исходов также n 20 , число не сдавших студен-

 

m

 

5. Тогда вероятность P(

 

)

5

0,25.

 

 

 

тов

A

A

 

 

 

 

 

 

 

 

20

 

 

 

 

 
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности