
2 семестр - Математика 2-ая контрольная
.pdf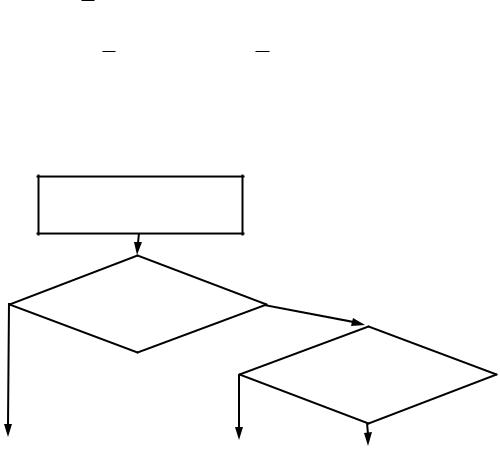
10
В данном случае события: «студент сдал экзамен» (А) и «студент не сдал экзамен» ( А ) являются противоположными, сумма их вероятностей равна 1.
P A P A 1, откуда P A 1 P A .
В некоторых задачах при расчете числа исходов следует применять формулы комбинаторики.
Выбор вида комбинаций элементов удобно проводить по блоксхеме (рис. 1).
Комбинации из n элементов по k
Все ли элементы |
|
|
Нет |
|
|
|
|
|||||
входят? |
|
|
|
|
|
|
|
|
|
|
||
Да |
|
|
|
|
Важен ли порядок |
|||||||
|
|
|
|
|
|
элементов? |
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Да |
|
|
|
Нет |
|
|
|
Перестановки |
|
Размещения |
|
Сочетания |
||||||||
Pn n! |
|
Ak |
|
|
n! |
|
C k |
|
n! |
|||
n n 1 n 2 ... 3 2 1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|||||||
|
n |
|
|
n |
|
|||||||
|
|
|
|
n k ! |
|
|
|
k! n |
k ! |
|||
|
Рис. 1. |
|
|
|
|
|
|
|
|
|
||
При использовании формул следует учитывать: |
0! 1, |
1! 1, |
||||||||||
2! 1 2 2 , 3! 1 2 3 6 и т.д.
Рассмотрим применение этих формул на следующем примере.
Пример 2.
Имеется четыре тома книг с номерами 1, 2, 3, 4. Сколькими способами можно:
1)расставить книги на полке;
2)выбрать из них любые два тома;
3)выбрать и расставить на полке два тома?
Решение.
1)В первом случае переставляем разными способами все кни-
ги, то есть в комбинацию входят все элементы – 4 книги. При этом на первое место можно поставить любой из четырех элементов

11
(книг), на второе – любой из оставшихся трех элементов, на третье – из двух, на четвертое – остается один элемент. Таким образом, число способов расстановки книг на полке равно 4 3 2 1 4! 24 – числу перестановок из всех четырех имеющихся элементов
( Р4 4!).
2) Во втором случае, выбираем две книги из четырех, имеем дело с комбинациями, в которые входят не все элементы из четырех, а только два элемента. Эти комбинации отличаются друг от друга хотя бы одним элементом, причем порядок не важен. Число таких комбинаций определяется как число сочетаний из четырех элементов по два:
C 2 |
|
4! |
|
|
4! |
|
1 2 3 4 |
6 . |
2! 4 2 ! |
|
|
||||||
4 |
|
|
2! 2! |
1 2 1 2 |
||||
|
|
|
||||||
3) В третьем случае при расстановке трех книг на полке выбираем из четырех элементов по два элемента, но учитываем порядок этих выбранных элементов. Число комбинаций, отличающихся либо элементом, либо их порядком – это есть число размещений из четырех элементов по два:
A2 |
|
|
4! |
|
|
1 2 3 4 |
12 . |
4 |
2 ! |
|
|||||
4 |
|
|
1 2 |
||||
|
|
|
|||||
Пример 3.
Имеются три разрезные буквы: М, Л, Е. Буквы перемешиваются, и случайным образом составляется слово. Найти вероятность, что получено слово «МЕЛ».
Найдем общее число исходов n. Три имеющиеся буквы переставляются, число комбинаций равно числу перестановок:
n P3 3! 1 2 3 6.
Благоприятный исход – получить заданное слово – один. То есть m 1.
Искомая вероятность P mn 16 .

12
Пример 4.
Из разрезных букв сложено слово «ЗАВОД». Из них наугад выбирается четыре буквы и составляется слово. Найти вероятность, что получено слово «ВОДА».
Найдем общее число исходов n. Из имеющихся пяти букв выбираем четыре, причем их порядок имеет значение. Число исходов найдем как число размещений
n A4 |
|
|
5! |
|
|
1 2 3 4 5 |
120 . |
5 |
4 ! |
|
|||||
5 |
|
1 |
|
||||
|
|
|
|||||
Благоприятный исход – получить заданное слово – один. То есть m 1.
Искомая вероятность P mn 1201 .
Пример 5.
В урне 3 белых и 4 черных шара, наугад достают 3 шара. Найти вероятности следующих событий:
1)А – все шары белые;
2)В – все шары черные;
3)С – все одного цвета;
4)D – есть ровно один белый шар, остальные – другого цвета;
5)Е – есть ровно два белых шара;
6)G – есть хотя бы два белых шара;
7)F – нет черного шара.
Решение.
Найдем общее число исходов. Вынимаем 3 шара из 7, порядок не имеет значения, используем формулу для подсчета сочетаний:
n C3 |
|
7! |
|
|
7! |
|
5 6 7 |
35 . |
3! 7 3 ! |
|
|
||||||
7 |
|
|
3! 4! |
1 2 3 |
||||
|
|
|
||||||
Найдем благоприятные исходы для каждого события и их вероятности.
1) А – все шары белые, то есть достают 3 белых шара из име-
ющихся трех белых: |
|
|
m A |
|
|
|
|
|
|
|
|
|
||
m A C3 |
1, |
P A |
|
|
1 |
. |
|
|
|
|
||||
|
|
|
|
|
||||||||||
3 |
|
|
|
|
n |
35 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
2) В – все шары черные, то есть достают 3 черных шара из |
||||||||||||||
имеющихся 4-х: |
|
|
|
|
|
m B |
|
|
|
|
||||
m B C3 |
|
4! |
|
4 , P B |
|
|
4 |
. |
||||||
|
|
|
|
|||||||||||
4 |
|
3! 1! |
|
|
n |
|
35 |
|||||||
13
3) С – все одного цвета, то есть или все белые, или все черные.
Достают три белых шара из трех или три черных шара из четырех. |
|||||||
m С C3 |
С3 |
1 4 5, P С |
m С |
|
|
5 |
. |
|
|
||||||
3 |
4 |
|
n |
35 |
|||
|
|
|
|||||
4) D – есть ровно один белый шар, остальные (два) – другого
цвета. В этом случае достают один белый шар из трех белых и два черных из четырех черных.
m D C1 |
C2 |
|
3! |
|
|
4! |
|
3 6 18 , P D |
m D |
|
18 |
. |
3 |
4 |
1! 2! |
|
2! 2! |
|
n 35 |
||||||
|
|
|
|
|||||||||
5) Е – есть ровно два белых шара. В этом случае достают два
белых шара из имеющихся трех белых и один черный шар из четырех черных.
m Е C2 |
C1 |
|
3! |
|
|
4! |
|
3 4 12 , P Е |
m Е |
|
|
|
12 |
. |
2! 1! |
1! 3! |
|
|
|||||||||||
3 |
4 |
|
|
|
n |
|
35 |
|||||||
6) G – есть хотя бы два белых шара означает, что есть два белых шара или больше. В данном случае: есть два белых шара и один черный или есть три белых шара.
m G C2 |
C1 |
C3 |
3! |
|
4! |
1 3 4 1 12 1 13 |
, |
||||||||
|
|
|
|
|
|||||||||||
3 |
4 |
3 |
2! 1! |
1! 3! |
|
||||||||||
P G |
m G |
|
|
13 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
n |
|
|
35 |
|
|
|
|
|
|
|
|
|
||
7) F – нет черного шара, то есть достают три шара из не чер- |
|||||||||||||||
ных шаров, которых три штуки. |
|
||||||||||||||
m F C3 |
1, |
|
P F |
m F |
|
1 |
. |
|
|||||||
|
|
|
|
||||||||||||
3 |
|
|
|
|
|
|
n |
35 |
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
ЗАДАЧА 5. Составить ряд распределения дискретной случайной величины, найти ее математическое ожидание и дисперсию.
Предварительно рассмотрим вероятность суммы и произведения событий.
Суммой двух событий А и В называется событие С, которое заключается в том, что произошло или событие А, или событие В, или оба эти события вместе. При этом вероятность суммы несов-
местных событий равна сумме вероятностей этих событий:
Р С Р А В Р А Р В .
Это положение иллюстрируется следующей ситуацией. Студент сдает экзамен на оценку «удовлетворительно» с вероятностью 0,5; на оценку «хорошо» с вероятностью 0,3; на оценку «отлично» с

14
вероятностью 0,2. Какова вероятность того, что он сдаст экзамен на «хорошо» или «отлично»? Здесь – событие А – получил «хорошо», а событие В – получил «отлично», и эти события не могут произойти одновременно, то есть они несовместны. Событие С – получил или «хорошо», или «отлично» является суммой событий А и В. Поэтому
вероятность |
этого |
события |
Р С Р А В Р А Р В 0,3 0,2 0,5. |
|
|
Произведением двух событий А и В называется событие С, которое заключается в том, что произошло и событие А, и событие В, то есть оба эти события произошли вместе. Если события происходят независимо друг от друга, то вероятность их произведения рав-
на произведению вероятностей
Р С Р А В Р А Р В .
Например, известно, что студент получит зачет по математике с вероятностью 0,6, а зачет по иностранному языку с вероятностью 0,7. Найти вероятность того, что он получит оба зачета. Здесь событие А – студент получит зачет по математике, событие В – получит зачет по иностранному языку, и эти события независимые. Тогда событие С, которое заключается в том, что студент получит и пер-
вый зачет, и второй, есть С А В . Вероятность этого события
Р С 0,6 0,7 0,42.
Случайной величиной называется величина, которая в результате опыта может принять то или иное (но только одно) числовое значение, причем заранее, до опыта, не известно, какое именно.
Случайные величины обозначаются заглавными буквами конца латинского алфавита – X, Y.
Дискретной, то есть прерывной, называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.
Например, дискретная случайная величина X – оценка на экзамене, может принимать значения 2, 3, 4, 5. Допустим, что вероятность получить «2» – P X 2 0,2 , вероятность получить «3» –
P X 3 0,4, P X 4 0,3, P X 5 0,1.
Рядом распределения дискретной случайной величины называется таблица, в которую записываются все возможные значения случайной величины и соответствующие им вероятности.
xi 2 3 4 5

15
pi 0,2 0,4 0,3 0,1
Очевидно, что сумма вероятностей pi 1.
Для краткого описания случайной величины служат числовые характеристики: математическое ожидание, дисперсия и среднее квадратическое отклонение.
Математическое ожидание равно среднему значению случайной величины, находится по формуле:
M X x1 pi x1 p1 x2 p2 ... xn pn .
Имеем: M X 2 0,2 3 0,4 4 0,3 5 0,1 3,3 балла.
Дисперсия служит для оценки разброса значений случайной величины относительно среднего значения, находится по формуле:
D X xi2 pi M x 2 .
D X 22 0,2 32 0,4 42 0,3 52 0,1 3,32 0,81.
Среднее квадратическое отклонение показывает, на сколько в среднем отклоняются значения случайной величины от их среднего значения, находится по формуле:
X 
 D X , имеет размерность случайной величины. Имеем: X
D X , имеет размерность случайной величины. Имеем: X 
 0,81 0,9 балла.
0,81 0,9 балла.
Пример 1.
Рабочий обслуживает два станка. В течение смены первый станок потребует внимания рабочего с вероятностью 0,2, второй – с вероятностью 0,3. Составить ряд распределения числа станков, потребовавших внимания рабочего в течение смены. Вычислить его числовые характеристики.
Решение. Дискретная случайная величина Х – число станков, потребовавших внимания рабочего, может принимать значения 0, 1,
2.
Обозначим событие Аi – внимание потребовал i-й станок, то-
|
|
|
|
|
|
|
|
|
|
гда, Ài – |
i-й станок не |
потребовал внимания |
рабочего. Итак, |
||||||
Р А1 0,2 , |
P( |
|
|
Р А2 0,3; |
|||||
A1 ) 1 Р А1 0,8; |
|||||||||
P( |
|
2 ) 1 Р А2 0,7 . |
|
|
|||||
A |
|
|
|||||||
|
|
|
|
Найдем вероятность того, что случайная величина Х примет |
|||||
возможные значения 0, 1, |
2. |
|
|||||||

16
X 0 : (и первый станок не потребовал внимания, и второй не потребовал) А1 А2 .
P( X 0) P( A1 A2 ) P( A1) P( A1) 0,8 0,7 0,56.
X 1: (первый потребовал и второй не потребовал, или наоборот) A1 A2 A1 A2 .
P( X 1) P( A1 ) P( A2 ) P( A1 ) P( A2 )
0,2 0,7 0,8 0,3 0,14 0,24 0,38.
X 2: (и первый потребовал внимания, и второй) А1 А2 .
P( X 2) P( A1) P( A2 ) 0,2 0,3 0,06.
Составим ряд распределения:
xi |
0 |
1 |
2 |
pi |
0,56 |
0,38 |
0,06 |
3
Контроль: pi 0,56 0,38 0,06 1.
i 1
Вычислим числовые характеристики. Математическое ожидание
n
М ( Х ) xi pi 0 0,56 1 0,38 2 0,06 0,5. i 1
Дисперсия
D X x 2 |
p M X 2 |
02 0,56 12 0,38 22 0,06 0,52 0,37. |
|||
i |
|
i |
|
||
Среднее квадратическое отклонение |
|||||
( X ) |
|
|
|
0,61. |
|
|
D( Х ) |
|
0,37 |
||
Пример 2.
Студент сдает три экзамена в сессию. Вероятность сдать математику равна 0,8; вероятность сдать физику – 0,7; вероятность сдать историю –0,9. Случайная величина X – число сданных в сессию экзаменов. Составить ряд распределения, найти числовые характеристики.
Решение.
Случайная величина может принимать значения X= 0, 1, 2, 3. Обозначим события: А1 – сдал математику (М), А2 – сдал фи-
17
зику (Ф), А3 – сдал историю (И). Соответственно имеем: А1 – не сдал математику, А2 – не сдал физику, А3 – не сдал историю.
Вероятности этих событий:
Р А1 0,8, Р А1 1 0,8 0,2 , Р А2 0,7, Р А2 1 0,7 0,3 ,
Р А3 0,9 , Р А3 1 0,9 0,1.
Найдем вероятности.
X 0: (ничего не сдал, то есть, не сдал М и не сдал Ф и не сдал И) А1 А2 А3.
Р X 0 0,2 0,3 0,1 0,006 .
X 1: (сдал один экзамен, то есть, сдал М и не сдал Ф и не сдал И, или не сдал М и сдал Ф и не сдал И, или не сдал М и не сдал Ф и сдал И)
А1 А2 А3 А1 А2 А3 А1 А2 А3
Р X 1 0,8 0,3 0,1 0,2 0,7 0,1 0,2 0,3 0,9 0,092 .
X 2: (сдал два экзамена, то есть сдал М и сдал Ф и не сдал И, или сдал М и не сдал Ф и сдал И,
или не сдал М и сдал Ф и сдал И).
А1 А2 А3 А1 А2 А3 А1 А2 А3 .
Р X 2 0,8 0,7 0,1 0,8 0,3 0,9 0,2 0,7 0,9 0,398 .
X 3: (все сдал, то есть, сдал М и сдал Ф и сдал И) А1 А2 А3.
Р X 3 0,8 0,7 0,9 0,504 .
Составим ряд распределения:
xi |
0 |
1 |
2 |
3 |
pi |
0,006 |
0,092 |
0,398 |
0,504 |
3
Контроль: pi 0,006 0,092 0,398 0,504 1. i 1
Вычислим числовые характеристики. Математическое ожидание
18
n
М ( Х ) xi pi 0 0,006 1 0,092 2 0,398 3 0,504 2,4. i 1
Дисперсия
D X xi2 pi M X 2
02 0,006 12 0,092 22 0,398 32 0,504 2,42 0,46.
Среднее квадратическое отклонение
( X ) 
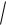 D( Х )
D( Х ) 
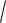 0,46 0,68.
0,46 0,68.
Пример 3. Выпускник вуза хочет устроиться на работу на одно из 3 предприятий. Вероятность трудоустройства на каждое из них равна 0,6. Случайная величина X – число предприятий, которое посетил студент, причем, если студента взяли на работу на одном предприятии, на другое он уже не идет. Составить закон распределения случайной величины X.
Решение. Случайная величина Х может принимать значения X 1, 2, 3. Пусть событие А – студента взяли на работу, A – не взяли (противоположное событие).
Вычислим вероятность значений случайной величины:
X 1 – студента взяло на работу первое предприятие.
P( X 1) P( À) 0,6 .
X 2 – на первом предприятии отказали и взяли на втором.
P( X 2) P( A À) 0,4 0,6 0,24.
X 3 – на первом предприятии отказали, и на втором отказали, и взяли на третьем; или на всех трех отказали.
P( X 3) P( A A À A A À) 0,4 0,4 0,6 0,4 0,4 0,4 0,16.
Ряд распределения
xi |
1 |
2 |
3 |
pi |
0,6 |
0,24 |
0,16 |
3
Контроль: pi 0,6 0,24 0,16 1.
i 1
Математическое ожидание
n
М ( Х ) xi pi 1 0,6 2 0,24 3 0,16 1,56. i 1
Дисперсия

19
D X xi2 pi M X 2
12 0,6 22 0,24 32 0,16 1,562 0,5664.
Среднее квадратическое отклонение
( X ) 
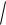 D( Х )
D( Х ) 
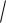 0,5664 0,75.
0,5664 0,75.
ЗАДАЧА 6. Найти среднее значение, дисперсию и среднее квадратическое отклонение для выборок.
Пример.
а) X – зарплата работников, X 10,12, 20, 25 тыс. руб. Выборка несгруппированная, найдем требуемые характери-
стики по следующим формулам. |
|
|
|
|
||||||||
Среднее значение x |
xi , где n – число наблюдений. |
|||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
Средняя зарплата x |
10 12 20 25 |
16,75 |
тыс. руб. |
|||||||||
|
||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
Дисперсия выборки S 2 |
xi x 2 |
|
|
|
||||||||
|
|
|
|
|
|
|
x |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 16,75 2 12 16,75 2 20 16,75 2 25 16,75 2 |
36,69. |
|||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
Среднее квадратическое отклонение |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
S 2 |
|
|
|
|
|
||||
S |
x |
36,69 |
6,06 тыс.руб. |
|
|
|
|
|||||
|
|
x |
|
|
|
|
|
|
|
|
||
б) Три работника получают по 10 тыс. руб., пять работников – по 15 тыс. руб, два – по 30 тыс. руб.
Выборка сгруппированная, найдем требуемые характеристики по следующим формулам.
Среднее значение |
x xi |
mi , где n – общее число наблюде- |
|||||
|
|
|
n |
|
|
||
ний; xi .– значение величины; |
mi – частота, |
которая показывает, |
|||||
сколько раз появилось значение xi . |
|
|
|||||
Составим таблицу |
|
|
|
|
|
||
|
xi |
|
10 |
15 |
|
30 |
|
|
mi |
|
3 |
6 |
|
2 |
|
