
Основы ТМ
.pdf
с некоторой погрешностью приравниваются соответствующие параметры экспериментального распределение и генеральной совокупности:
|
→ → |
(3.23) |
σo ≈ σ |
X o ≈ X . |
Для практических расчётов при n > 20 целесообразнее использовать более точные соотношения с учётом погрешности эмпирических параметров распределения:
|
σ |
|
→ |
|
σ . |
(3.24) |
σo = σ ± |
; |
X0 |
= X ± |
|||
|
2n |
|
|
|
n |
|
С учётом того, что при проведении расчётов используются экспериментальные данные, уравнения для теоретической и эмпирической кривых записываются относительно друг друга:
|
|
|
|
|
|
→ |
|
|
|
K′ |
|
|
1 |
− |
( x−x0 )2 |
|
(3.24) |
y = |
= σ |
|
2σ 2 |
|||||
n C |
0 |
2π e |
|
0 . |
||||
|
u |
|
|
|
|
|
|
|
где К – теоретическая частота попадания размера в интервал; Си – цена деления интервала по оси абсцисс.
Тогда из формулы (3.24) записывается уравнение для определения теоретической частоты попадания размера в определённый интервал:
|
|
|
|
|
|
→ |
|
|
n C |
|
|
1 |
− |
( x−x0 )2 |
|
|
|
|
2σ 2 |
||||
K′ = |
σ0 |
u |
= |
2π e |
0 . |
||
Для упрощения расчётов используется подстановку:
→
t = x − X .
σo
И после преобразования получается:
|
n C |
|
1 |
− |
t 2 |
|
|
|
|
||||
K′ = |
σ0 |
u = |
2π e |
2 . |
||
Вводится ещё одно условное обозначение:
1 |
e− |
t 2 |
|
|
= Zt . |
||
2 |
|||
2π |
|
|
|
(3.25)
(3.26)
(3.27)
(3.28)
Окончательно уравнение (3.25), с учётом положений уравнения (3.23), принимает следующий вид:
71

K′ = |
n C |
u |
Zt . |
(3.29) |
|
σ |
t |
|
|||
|
|
|
|
|
|
Величина Zt определяется в зависимости от t и находится по справочникам. По полученным значениям K строится теоретическая кривая распределения размеров исследуемой партии деталей (кривая 2 на рис. 3.25, см. с. 69).
Однако для того, чтобы использование равенств (3.23) и (3.24) было достаточно обоснованным, необходимо убедиться в том, что:
а) используемая для анализа выборка деталей действительно подчиняется закону нормального распределения;
б) она действительно является случайной.
Первоначально проверяется выборка на соответствие закону нормального распределения.
В математической статистике для проверки нормальности распределения выборки используется несколько критериев. Наиболее простым для вычислений является критерий академика А.Н.Колмогорова λ. Этот критерий используется для анализа нормальности распределения приведенной выше выборки размеров.
Первоначально делается предположение о том, что партия деталей, из которой извлечена выборка, имеет нормальное распределение, следовательно, равенства (3.23) и (3.24) справедливы. Согласно этой методике:
λ = |
Nx − Nx′ max , |
(3.30) |
|
n |
|
где N = ∑mi – накопленные эмпирические частоты распределения случайной
величины xi, которые подсчитываются в рассматриваемом примере по данным таблицы (столбец 3);
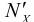 – накопленные теоретические частоты распределения;
– накопленные теоретические частоты распределения;
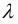 – случайная величина (критерий согласия), которая подчиняется закону нормального распределения, по которому можно
– случайная величина (критерий согласия), которая подчиняется закону нормального распределения, по которому можно
вычислить вероятность этой величины 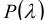
В числителе формулы (3.30) берётся наибольшая абсолютная разность накопленных теоретических и эмпирических частот. Накопленные теоретические частоты подсчитываются на основе формулы (3.29). Как видно из таблицы (колонка 10), максимальная разность частот равна 1,521 и тогда:
λ = 1,52150 ≈ 0,214 .
P(λ) – выражает вероятность соответствия эмпирического распределения, полученного в примере, распределению генеральной совокупности. Для анализа распределений, рассматриваемых в технике, установлено, что если Р(λ) < 0,05 (то есть вероятность соответствия очень мала), то первоначальное предположение об отсутствии различия между распределениями выборки и генеральной совокупно-
72
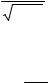
сти является неверным. И наоборот, если Р(λ) > 0,05, то полученное расхождение между эмпирическими и теоретическими частотами считается случайным, а первоначальное предположение верным.
Для рассматриваемого примера согласно таблице при λ = 0,214 Р(λ)=1,0, то есть в данном случае имеет место достоверность, следовательно, сделанное в начале проверки предположение о соответствии распределения размеров исследуемой выборки нормальному закону является верным.
Проверка предположения о случайности выборки осуществляется в исследованиях тогда, когда в течение наблюдения за получаемыми размерами центр распределения величины X может постепенно меняться, однако среднее квадратичное отклонение σ при этом остается постоянным. Именно такие явления наблюдаются на операциях механической обработки в силу действия ряда закономерноизменяющихся погрешностей (например, погрешности из-за размерного износа инструментов).
Достаточно простым и надёжным способом для проверки случайности выборки является способ последовательных разностей.
Этот способ основан на определении некоторого критерия:
|
с |
2 |
|
|
|
|
|
1 |
|
n−1 |
|
τ = |
|
>τg , причем C2 = |
|
∑ai2 |
, |
||||||
S |
2 |
2(n − |
|
||||||||
|
|
|
|
|
|
|
1)i =1 |
|
|||
|
|
|
|
2 |
|
1 |
n |
→ 2 |
|
|
|
|
|
|
S |
|
= |
|
∑ xi − X , |
|
|
(3.31) |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
n −1 i =1 |
|
|
|
|
|
где 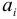 – определяется из следующих соотношений:
– определяется из следующих соотношений:
ai |
= x2 − x1 |
a13 = x14 − x13 |
, |
||||
a |
= x |
− x |
a |
n−1 |
= x |
− x |
−1 |
i |
3 |
3 |
|
n |
n |
||
где 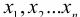 – порядковые номера деталей в выборке;
– порядковые номера деталей в выборке;
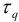 – некоторое критическое значение
– некоторое критическое значение 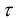 .
.
Известно, что при n > 20 критерий 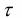 имеет нормальное распределение, если выборка, для которой он определён, действительно случайна. Поэтому проверка случайности выборки сводится к сравнению
имеет нормальное распределение, если выборка, для которой он определён, действительно случайна. Поэтому проверка случайности выборки сводится к сравнению 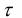 и
и 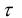 . Если
. Если 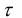 >
>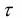 , то гипотеза случайности выборки верна, если
, то гипотеза случайности выборки верна, если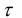 <
<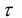 , то неверна.
, то неверна.
Для расчёта 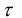 используется выражение:
используется выражение:
τq =1− |
tg . |
(3.32) |
|
n +1 |
|
В свою очередь величина 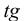 находится по таблице, если известно что:
находится по таблице, если известно что:
Ф(tg)= 0.5 −100q .
Величина 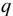 называется уровнем значимости и, при технических расчётах, принимается равной 5%.
называется уровнем значимости и, при технических расчётах, принимается равной 5%.
73

Далее определяется значение 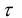 для рассматриваемого примера:
для рассматриваемого примера:
С2=0,0014; S2=0.0012; Τ=1.17.
Определяется значение 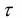 при уровне значимости в 5 %, для этого сначала находится:
при уровне значимости в 5 %, для этого сначала находится:
Ф(tg)= 0.5 −1005 = 0,45 .
Далее, по таблице (например, И.О. Солонин «Применение математической
статистики в технологии машиностроения». Приложение 1) определяется 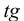 =1.65 и, следовательно:
=1.65 и, следовательно:
τq =1−1.5165 = 0.74 .
Таким образом 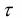 >
> 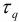 . Следовательно, выборка является случайной. Выполненные проверки позволяют перейти к использованию закона нормаль-
. Следовательно, выборка является случайной. Выполненные проверки позволяют перейти к использованию закона нормаль-
ного распределения для анализа точности обработки исследуемой партии деталей. В связи с тем, что рассеяние размеров на исследуемой операции подчиняется закону нормального распределения, следовательно, практические размеры деталей могут находиться в пределах поля, ограниченного теоретической кривой. Годными же будут те детали, размеры которых будут находиться в пределах поля до-
пуска (рис. 3.25, см. с. 69).
Вероятность получения количества деталей в пределах поля допуска равна отношению площади, заключенной между ординатами, проведенными через границы поля допуска и границы теоретической кривой 2 (рис. 3.25, см. с. 69) ко всей площади, ограниченной кривой распределения и осью абсцисс.
Для определения искомой площади используется нормированная функция Лапласа, которая получается после интегрирования уравнения кривой Гаусса (формула (3.32)), с использованием подстановки:
→
t = x − X . (3.33)
σo
После интегрирования уравнения кривой Гаусса получается:
|
1 |
t |
t 2 |
|
|
Ф(t)= |
∫e− |
|
dt . |
(3.34) |
|
2 |
|||||
|
2π |
0 |
|
|
|
Значения функции Лапласа табулированы. В приведённом виде формула (3.34) используется для определения половины площади под кривой Гаусса, так как:
t → ∞, Ф(t)→ 0.5
Для получения значения всей площади под кривой Гаусса используется удвоенное значение функции Лапласа:
74
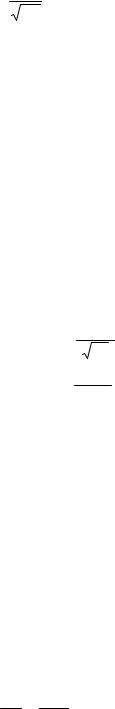
Ф(t)= |
1 |
t |
− |
t 2 |
|
|
∫e |
|
dt =1 при ∞ < t < +∞ . |
(3.35) |
|||
2 |
||||||
|
2π |
0 |
|
|
|
|
Для практических расчетов чаще всего используется диапазон кривой Гаусса в пределах – 3 < t < +3. При этом 2Ф(3) = 0,9973 или (в процентах) в указанном интервале содержится 99,73 % всей площади под кривой Гаусса.
Поскольку (x–X) = 3σ, то следовательно, для практических целей используется диапазон (x–X)max = +/– 3σ. Отсюда следует, что если Т = 6σ, то вероятное количество годных деталей будет составлять 99,73 % от всей исследуемой партии.
В примере площадь под кривой Гаусса в пределах поля допуска расположена несимметрично относительно величины X, и поэтому определение величины площади необходимо произвести для левой и правой частей кривой Гаусса отдельно.
Первоначально определяется значение аргумента t по формуле (3.26), при этом для получения наиболее достоверных данных следует использовать формулы (3.24). Тогда получаются следующие значения генеральной совокупности:
X |
0 |
=15.98 ± 0.035 |
=15.98 ± 0.005 |
|
→ |
|
|
|
|
|
|
|
50 |
. |
|
|
|
0.035 |
|
σ0 |
= 0.035 ± |
= 0.035 ± 0.0035 |
||
|
|
|
10 |
|
Ожидаемое количество бракованных деталей в исследуемой партии определяется по следующей формуле:
W = [1−Ф(tл )−Ф(tп )] 100% , |
(3.36) |
где 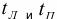 – значения аргумента t соответственно для левой и правой границ поля допуска.
– значения аргумента t соответственно для левой и правой границ поля допуска.
При полученных колебаниях значений Xо и σо величина брака будет коле-
баться от Wmax = 19,75 % до Wmin = 5.95 %.
Полученный результат следует оценить как неудовлетворительный, так как процент бракованных деталей оказался, весьма высок. Об этом свидетельствует и такая характеристика как коэффициент точности операции:
µ = 6Tσ = 00..2111 ≈1.9 при Т = 6σ µ = 1.
Причиной брака может быть влияние погрешностей: систематических, случайных, либо их совместное действие.
Так, если (рис. 3.26, а, см. с. 76) при заданном допуске Т распределение размеров будет соответствовать кривой 2 (при 6σ > T), то причиной брака в этом случае будет действие случайных погрешностей, источником которых, как указано выше, может быть колебание припуска, колебание твёрдости заготовок, низкая жесткость станка и т.д.
75
Именно такой случай имел место в рассмотренном примере. Следовательно, уменьшение качества бракованных деталей может быть достигнуто за счёт воздействия на источники случайных погрешностей
При величинах Т = 6σ и µ = 1 точность операции считается достаточной. Однако на практике возможен брак даже и при достаточной точности процесса. Действие систематических погрешностей постоянного характера, например, приводит к смещению кривой Гаусса (кривая 3, рис. 3.26, б) относительно середины поля допуска. При этом может выполняться условие Т = 6σ, однако X получает приращение на величину ∆, которая возникает в результате появления погрешности, допущенной при настройке станка.
Рис. 3.26. Влияние погрешностей обработки на положение кривой Гаусса
В соответствии с рис. 3.26 это приращение ∆ = /X–Аср/. Тогда в рассматриваемом примере получается:
∆=15,98-15,975=0,005,
∆доп = |
|
E −6σ |
|
|
= |
|
|
0.11−0.21 |
|
|
= 0.05 . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
2 |
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
||||
Для работы без брака должно выполняться условие ∆ ≤ ∆доп., что в данном примере выполняется. Изменение настройки станка с целью исключения погрешности настройки (∆ = 0) не позволяет освободиться от брака. Об этом можно судить и по коэффициенту точности настройки:
l = |
∆ ≤ lдоп |
|
|
l = |
0.005 |
≈ 0.045 , |
|||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
T |
|
|
|
|
|
0.11 |
|
|
|
|
||||||
lдоп = |
|
T −6σ |
|
|
= |
|
|
1− µ |
|
= |
|
|
1−1.9 |
|
|
= 0.45. |
|||
|
|
|
|
|
|
||||||||||||||
|
|
2T |
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
Следовательно, в данном случае выполняется условие l < lдоп.
76
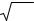
Основные мероприятия по уменьшению брака на рассмотренной операции должны быть направлены на уменьшение величины коэффициента точности µ и соответственно, величины σ, которая зависит от величины случайных погрешностей. Условия работы без брака характеризуются следующими значениями коэффициентов:
µ ≤ 1; L ≤ Lдоп . |
(3.37) |
Если неравенства (3.37) не выполняются, то возможен брак. Процент годных деталей определяется по следующей формуле:
T / 2 |
− ∆ |
−T / 2 |
− ∆ |
, |
(3.38) |
|||
W = ф |
|
|
|
−ф |
|
|
||
σ |
|
σ |
||||||
|
|
|
|
|
|
|
||
где T / 2 − ∆ – координата верхней границы поля допуска относительно середины поля рассеивания размеров;
−T / 2 − ∆ – координата нижней границы поля допуска относительно середины поля рассеивания размеров.
Процент исправимого и неисправимого брака в исследуемой партии деталей определяется по следующим формулам:
|
T / 2 − ∆ |
, |
|
||||
Wисп = 0,5 −ф |
|
|
|
|
|||
σ |
|
|
|||||
|
−T / 2 |
− ∆ |
|
||||
Wнеисп = 0,5 |
−ф |
|
|
|
|
. |
(3.39) |
|
σ |
|
|
||||
|
|
|
|
|
|
||
5.3.3. Рассеивание размеров партии деталей при действии доминирующих факторов
При обработке партии деталей на рассеяние их размеров иногда может оказывать влияние один доминирующий фактор.
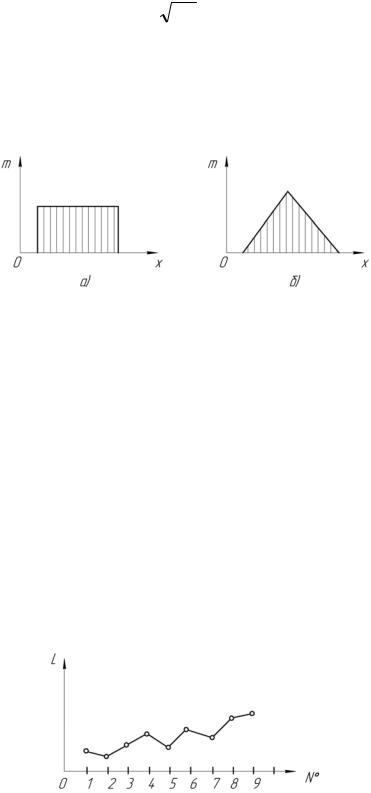
Например, при доминирующем влиянии тепловых деформаций станка во время повышения температуры, в начальный период работы (рис3.23, а, см. с. 65), распределение размеров в партии заготовок может соответствовать закону равной вероятности (рис. 3.27, а, см. с. 78).
В этом случае величина фактического поля рассеяния определяется по форму-
ле:
w = 2 3σ . |
(3.30) |
Если изменение размеров заготовок, вызываемое износом инструмента, имеет закономерность, представленную на рис. 3.23, б, то распределение размеров может выражаться законом Симпсона (рис. 3.27, б, см. с. 78) и фактическое поле рассеивания определяется по следующей формуле:
77
w = 2 6σ . |
(3.31) |
Следует отметить, что при анализе точности обработки партии деталей на настроенных станках законы равной вероятности и Симпсона практически не могут быть использованы в "чистом" виде, так как всегда имеются случайные погрешности, деформирующие их в направлении закона нормального распределения.
Рис. 3.27. Законы распределения размеров:
а) равной вероятности; б) закон Симпсона
5.3.4. Метод точечных диаграмм
Метод кривых распределения обладает тем недостатком, что не учитывает последовательность обработки деталей, т.е. не даёт представления о распределении погрешностей обработки во времени.
Метод точечных диаграмм позволяет отделить случайные погрешности от систематических погрешностей, даёт наглядное представление о резких отклонениях в ходе процесса и времени их появления. Точечная диаграмма (рис. 3.28) строится по ходу обработки всей партии в координатах: номер заготовки (№), размер заготовки (L).
Рис. 3.28. Точечная диаграмма изменения размеров заготовок
Если при обработке партии деталей на точность выполнения размеров влияют только случайные факторы, то точечные диаграммы не дают дополнительной информации о точности операции по сравнению с кривыми распределения. Если же при обработке будет действовать какая-либо доминирующая закономерно изме-
78

няющаяся погрешность (например, вызываемая износом режущего инструмента), то её влияние можно будет определить из точечной диаграммы (рис. 3.28).
При значительных колебаниях размера от заготовки к заготовки направление полосы рассеяния на малом участке выявить трудно. В этом случае на точечной диаграмме откладываются размеры не каждой заготовки, а средний размер группы из нескольких заготовок. И тогда тенденция изменения размеров во времени выявляется более отчетливо, так как рассеяние средних групповых размеров меньше, чем рассеяние отдельных размеров.
Так, если рассеивание размеров подчиняется нормальному закону распределения со средним квадратичным отклонением σ, то рассеивание средних групповых размеров также будет подчиняться нормальному закону:
σгр = |
σ |
, |
(3.32) |
|
n |
|
|
где n-число заготовок в группе.
Построение точечных диаграмм широко практикуется при статистическом контроле хода операций. При таком контроле проверяются не все заготовки, а лишь определенная часть (обычно не более 25%).
Из общего потока заготовок последовательно выделяются определённые группы – пробы и по результатам их измерения строится точечная диаграмма (рис. 3.29).
Выход среднего группового размера X за контрольные границы (Вк и Нк) служит сигналом для наступления периода подналадки станка.
Рис. 3.29. Точечная диаграмма, построенная по средним размерам групп
Положение верхней Вк и нижней Нк контрольных линий по отношению к границам поля допуска (Т) определяется следующей величиной:
|
− |
1 |
(3.33) |
e = 3σ −3σгр = 3σ 1 |
. |
||
|
|
n |
|
79
Раздел IV. КАЧЕСТВО ПОВЕРХНОСТЕЙ ДЕТАЛЕЙ МАШИН
1. ОСНОВНЫЕ ПОНЯТИЯ О КАЧЕСТВЕ ПОВЕРХНОСТИ
Одним из показателей качества в машиностроении является качество поверхности деталей машин. Важнейшие эксплуатационные характеристики машин и механизмов, такие как износостойкость, усталостная прочность, коррозионная стойкость, контактная прочность неподвижных соединений, качество посадок подвижных соединений зависят не только от размерной точности деталей, из которых эти машины собраны, но и от качества их поверхностей.
Впроцессе механической обработки деталей машин их поверхности подвергаются пластическому деформированию, абразивной обработке, обработке резанием, электрофизической или электрохимической обработке, при этом обрабатываемые поверхности приобретают реальный профиль с определенными физикомеханическими свойствами.
Вобщем случае качество поверхности готовой детали определяется как отклонение геометрических параметров реальной поверхности от номинальной. К таким геометрическим параметрам реальной поверхности относятся: шероховатость, волнистость и, в некоторых случаях, погрешность формы.
Помимо геометрических параметров, поверхностный слой обработанных деталей характеризуется физико-механическими свойствами, такими как твёрдость поверхностного слоя, микроструктура слоя и остаточные поверхностные напряжения. Также поверхностный слой деталей, кроме механических свойств, может приобретать отличные от основного материала химические свойства.
2. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ КАЧЕСТВА ПОВЕРХНОСТНОГО СЛОЯ
Основной геометрической характеристикой качества поверхностного слоя, используемой при проектировании и анализе действующих технологических процессов, является шероховатость поверхности.
Шероховатость поверхности представляет собой, с определённой приближённостью, геометрический след кромки режущего инструмента, оставленный в материале заготовки, и искаженный пластическими деформациями, сопутствующими процессу формообразования поверхности (рис. 4.1).
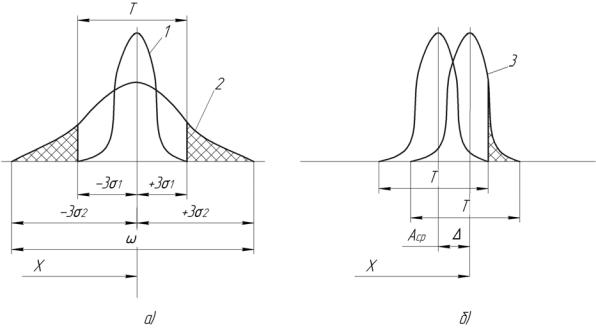
Принято шероховатость поверхности характеризовать отношением 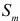 к высоте неровностей
к высоте неровностей 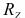 :
:
Sm |
p 50 . |
(4.1) |
|
||
Rz |
|
|
80
