корнюшин.численные методы

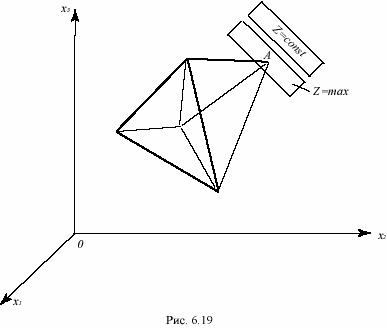
81

2) всякое линейное неравенство a1x1+a2x2+a3x3 ≤b (≥ b) изображается одним из двух

полупространств, на которые все пространство разбивается плоскостью a1x1+a2x2+a3x3=b (включая ее);

3) всякая система линейных неравенств-ограничений задачи

a11 x1 + a12 x2 + a13 x3 ≤ b1; a21 x1 + a22 x2 + a23 x3 ≤ b2 ;

...............................

am1 x1 + am2 x2 + am3 x3 ≤ bm

изображается множеством точек, заполняющих некоторый выпуклый многогранник (см. рис. 6.19), но которое, в частности, может оказаться пустым (тогда соответствующая задача неразрешима) либо быть бесконечным выпуклым многогранным множеством;

4) требование неотрицательности переменных x1 ≥ 0; x2 ≥ 0; x3 ≥ 0 означает, что многогранник ограничений расположен в первом октанте системы осей x1, x2, x3;

5)целевая функция Z=c1x1+c2x2+c3x3 изображается параллельно перемещающейся плоскостью c1x1+c2x2+c3x3=const (поверхность уровня целевой функции – см. рис.6.19);

6)максимум (минимум) целевой функции всегда достигается в какой-то вершине многогранника ограничений.

Если же задача линейного программирования выражается большим числом параметров, чем три, можно продолжать пользоваться геометрической терминологией, несмотря на то, что уже нет реальных геометрических образов и картин, которые бы изображали соответствующие понятия (имеющие чисто алгебраическую природу). Такое «геометрическое» мышление в многомерном пространстве удобно и полезно, т.к. оно позволяет ориентироваться в громоздких алгебраических преобразованиях, используемых в задачах линейного программирования.

Итак, можно сделать следующие обобщения.

1)Всякое линейное уравнение a1x1+a2x2+…+anxn=b «изображается» некоторой плоскостью (гиперплоскостью) в n-мерном пространстве осей x1, x2,…,xn.

2)Всякому линейному неравенству a1x1+a2x2+…+anxn ≤b (≥ b) соответствует одно из двух

полупространств, на которые гиперплоскость a1x1+a2x2+…+anxn=b делит все n-мерное пространство.

3)Всякой системе линейных неравенств-ограничений задачи

82

a11 x1 + a12 x2 +... + a1n xn ≤ b1; a21 x1 + a22 x2 +... + a2n xn ≤ b2 ;

...............................

am1 x1 + am2 x2 +... + amn xn ≤ bm

соответствует некоторый выпуклый гипермногогранник (в частности, это множество может быть пустым или бесконечным).

4) Неотрицательность x1 ≥ 0, x2 ≥ 0,..., xn ≥ 0 означает, что гипермногогранник ограничений лежит в первом гипероктанте осей x1, x2,…, xn.

5)Целевой функции Z=c1x1+c2x2+…+cnxn соответствует параллельно перемещающаяся гиперплоскость c1x1+c2x2+…+cnxn=const (поверхность уровня целевой функции).

6)Максимум (минимум) целевой функции всегда достигается в какой-то вершине гипермногогранника ограничений (но он может стать бесконечным, если область ограничений бесконечна).

4.6.2.5. Алгебраическая характеристика вершины многогранника ограничений

Чтобы получить такую характеристику, обратимся снова к двумерной картинке. В этом случае вершина соответствующего многоугольника есть точка пересечения каких-то его двух сторон (lr) и (ls), которые изображают границу r-го и s–го ограничений, т.е. имеют своими уравнениями прямые

(lr): ar1x1+ar2x2=br; (ls): as1x1+as2x2=bs.

В трехмерном случае (т.к. точка трехмерного пространства определяется пересечением трех плоскостей) вершину многогранника ограничений можно охарактеризовать уравнениями тех трех граней (Пr), (Пs) и (Пt), пересечением которых она является:

(Пr): ar1x1+ar2x2+ar3x3=br; (Пs): as1x1+as2x2+as3x3=bs; (Пt): at1x1+at2x2+at3x3=bt.

Заметим, что некоторые вершины могут попасть на одну из координатных плоскостей или на одну из координатных осей, как, например, в задаче 5 раздела 4.6.2.3. Для такой вершины будет выполняться одно или два из уравнений x1=0, x2=0, x3=0 (и если, в частности, начало координат является вершиной, то выполняются все три уравнения).

Наконец, в случае n-мерной задачи надо считать, что вершина характеризуется как пересечение соответствующих n гиперплоскостей (в том числе, возможно, и координатных гиперплоскостей).

Для дальнейшего будет удобно каждое ограничение

ai1x1+ai2x2+…+ainxn ≤bi (i=1,2,…,m)

записывать в виде

bi- ai1x1-ai2x2-…-ainxn ≥0

или, что то же самое, в виде

ai1(-x1)+ai2(-x2)+…+ain(-xn)+bi ≥0 (i=1, 2,…, m).

Будем рассматривать левую часть ограничения как новую переменную yi, т.е. положим

yi= ai1(-x1)+ai2(-x2)+…+ain(-xn)+bi (i=1, 2,…, m),

так что совокупность ограничений теперь запишется в виде y1 ≥ 0, y2 ≥ 0,..., ym ≥ 0,

а вместе с требованием неотрицательности получим единообразную запись для всех ограничений: x1 ≥ 0, x2 ≥ 0,..., xn ≥ 0, y1 ≥ 0, y2 ≥ 0,..., ym ≥ 0.

Заметим, что дополнительные переменные имеют простой экономический смысл. Так как

yi=bi-(ai1x1+ai2x2+…+ainxn),

то yi представляет собой остаток i-го производственного ресурса (из его запаса bi) после того, как при реализации плана x1, x2,…, xn он затрачен в количестве

ai1x1+ai2x2+…+ainxn.

83

После введения дополнительных переменных yi можно сказать, что каждая вершина многогранника ограничений обладает тем свойством, что в ней какие-то n из числа переменных x1, x2,…, xn, y1, y2,…, ym обращаются в нуль. Например, в задаче 1 раздела 4.6.2.3 (см. рис. 6.14) вершина А, как точка пересечения прямых (l1) и (l2), определяется тем, что в ней y1=0, y2=0, где через y1 и y2 обозначены: y1=5-(-x1+2x2), y2=7-(x1+x2), или в другой записи y1=-(-x1)+2(-x2)+5, y2=(- x1)+(-x2)+7. Точно также вершина В, как точка пересечения прямых (l2) и (l3), алгебраически характеризуется тем, что в ней y2=0, y3=0, где через y2 и y3 обозначены y2=(-x1)+(-x2)+7; y3=2(- x1)+9-x2)+11; вершина С (точка пересечения прямых (l3) и (l4)) характеризуется тем, что в ней

y3=0, y4=0, где y3=2(-x1)+(-x2)+11; y4=-(-x1)-2(-x2)-7.

В задаче 5 раздела 4.6.2.3 для вершины С (см. рис. 6.18) x11=0, y1=0, где

y1=(-x11)+(-x12)+3.

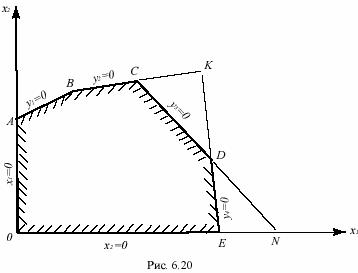
Итак, повторим снова, что в каждой вершине какие-то n переменных обращаются в нуль. Но обратное утверждение неверно. Если в какой-то точке n переменных из системы x1, x2,…, xn; y1, y2,…, ym обращаются в нуль, то эта точка необязательно является вершиной многогранника ограничений. Например, если многоугольник ограничений имеет вид OABCDE (рис. 6.20), то для вершины O x1=x2=0, для вершины E x2=y4=0, для вершины C y2=y3=0.

Но если рассмотреть точку К, в которой пересекаются продолжения отрезков BC и DE, то в ней будет y2=y4=0, хотя точка К не является вершиной рассматриваемого многоугольника. Точно так же набор x1=y3=0 не дает вершины, а дает точку N, в которой пересекаются несоседние стороны: x1=0 (ось x2) и y3=0 (прямая CD).

Как же алгебраически отличить набор, дающий вершину, от набора, не дающего вершины? Ответ на этот вопрос опять-таки подсказывается геометрией. Дело в том, что вершина характеризуется не только тем, что в ней какие-то n переменных обращаются в нуль, но и тем, что все остальные m переменных остаются неотрицательными, т.к. вершина принадлежит многограннику ограничений. А для такой точки, как торчка К на рис.6.20, две переменные (y2 и y4) обращаются в нуль, но не все остальные переменные остаются неотрицательными; например, для точки К будет y3 ≤ 0 , т.к. точка К лежит с той стороны от прямой y3=0, которая не заштрихована. Точно так же для точки N две переменные x1 и y3 обращаются в нуль, но y1<0 и y2<0. Все это связано, конечно, с тем, что точки К и N лежат вне многоугольника OABCDE.

Таким образом, всякая вершина многогранника ограничений вполне определяется тем, что

вней n переменных из числа x1, x2,…, xn; y1, y2,…, ym обращаются в нуль, а остальные m переменных остаются неотрицательными.

Если в данной вершине только n переменных из числа x1, x2,…, xn; y1, y2,…, ym обращаются

внуль и, следовательно, все остальные m переменных строго положительны, то будем называть такую вершину регулярной; если же в данной вершине обращаются в нуль больше, чем n переменных из числа x1, x2,…, xn; y1, y2,…, ym, то будем ее называть нерегулярной (или говорить, что

вэтой вершине имеет место вырождение).

84

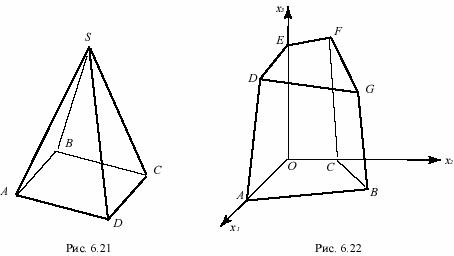
Например, если (в трехмерной задаче) многогранник – четырехгранная пирамида (рис. 6.21), то вершины A, B, C, D – регулярные вершины, а S – нерегулярная вершина. В многограннике же, изображенном на рис. 6.22, все вершины – регулярные.

Введем теперь важное в теории линейного программирования определение. Будем называть n переменных из числа x1, x2,…, xn; y1, y2,…, ym, которые обращаются в данной вершине многогранника ограничений в нуль, базисными переменными, остальные же m переменных –

внебазисными переменными.

Таким образом, понятие базисных и внебазисных переменных связывается с рассматриваемой вершиной многогранника ограничений – каждой вершине соответствует своя система базисных и внебазисных переменных, при переходе к другой вершине состав базисных и внебазисных переменных изменяется. Далее, в случае регулярной вершины базисные и внебазисные переменные определяются однозначно – те и только те m переменных, которые в регулярной вершине положительны, – это небазисные переменные, а те и только те n переменных, которые в ней обращаются в нуль, – это базисные переменные. В случае же нерегулярной вершины базисные и внебазисные переменные определяются неоднозначно, здесь переменных, обращающихся в нуль, в рассматриваемой вершине больше, чем n, но только некоторые n из их числа определяются как базисные переменные, а остальные m переменных, среди которых также имеются обращающиеся в этой вершине в нуль, определяются как внебазисные переменные. Именно это обстоятельство отмечается в задачах линейного программирования как «случай вырождения».

Нужно запомнить следующее: в регулярном случае все внебазисные переменные положительны, а в случае вырождения некоторые внебазисные переменные в данной вершине равны нулю.

4.6.3.Симплексный метод

4.6.3.1.Геометрическая подготовка

Пусть дана общая задача линейного программирования на максимум

при ограничениях

a11 x1 + a12 x2 +... + a1n xn ≤ b1;

am1 x1 + am2 x2 +... + amn xm ≤ bm

При помощи дополнительных переменных y1, y2,…,ym можно записать ограничения (2) в таком виде, как в предыдущем разделе:

ym = am1 (−x1 ) + am2 (−x2 ) +... + amn (−xm ) +bm ≥ 0.

Из геометрических соображений следует, что max Z достигается в какой-то вершине многогранника ограничений, т.е. в такой точке, для которой значения n переменных из числа x1, x2,…, xn; y1, y2,…, ym становятся равными нулю (базисные переменные), а значения прочих m переменных остаются неотрицательными (внебазисные переменные). Можно поэтому наметить такой общий ход решения задачи линейного программирования:

1)исходя из какой-то определенной вершины, т.е. исходя из какого-то набора базисных и внебазисных переменных, прежде всего выясним, не достигается ли максимум целевой функции именно в этой вершине;

2)если оказалось, что максимум еще не достигнут, то перейдем от данной вершины к другой и повторим прежний анализ.

Надо, однако, иметь в виду что даже при сравнительно небольших m и n (порядка 20 – 30) число вершин n–мерного гипермногогранника может быть чрезвычайно большим. Пожалуй, и современные быстродействующие ЭВМ не справятся с необходимыми вычислениями в разумное время, если стать на путь простого перебора всевозможных вершин. В связи с этим устанавливается такой порядок вычислений, который обеспечивает не простой переход от одной вершины к другой, а такой, при котором значение целевой функции «улучшается» (т.е. при задаче на максимум – увеличивается). В этом и заключается смысл так называемого метода последовательного улучшения плана в теории линейного программирования. По-видимому, проще всего будет переходить от данной вершины к какой-то соседней, причем следует иметь в виду, что

вслучае двумерной задачи каждая вершина имеет две соседние, а в случае пространства большего числа измерений вершина может иметь весьма много соседних. Но что такое «соседняя вершина»

вслучае n-мерной задачи? Для того чтобы это осмыслить, надо определить понятие «соседняя вершина» алгебраически. Нам известно, что одна вершина отличается от другой составом базисных и внебазисных переменных.

Рассмотрим пример. Для вершины А многоугольника (см. рис.6.20) базисными

переменными будут x1, y1, а внебазисными – x2, y2, y3, y4. Для вершины D базисными переменными будут y3, y4, а внебазисными – x1, x2, y1, y2 (и так же для остальных вершин). Возьмем теперь две соседние вершины, например, А и В. Для вершины A базисные переменные x1, y1; внебазисные – x2, y2, y3, y4. Для соседней вершины В базисные переменные y1, y2; внебазисные – x1, x2, y3, y4. Видно, что при переходе от А к В базисная переменная x1 становится внебазисной, а внебазисная переменная y2 становится базисной. То же самое имеет место в случае пространственного многогранника (см. рис.6.22). Например, если уравнения граней многогранника рис. 6.22

следующие: грань OEFC – x1=0; OADE – x2=0; OABC – x3=0; DEFG – y1=0; BGFC – y2=0; ABGD – y3=0, то для вершины С базисные переменные x1, x3, y2; внебазисные – x2, y1, y3; для соседней вершины О базисные переменные x1, x2, x3; внебазисные – y1, y2, y3. Замечаем, что при переходе от С к О переменные y2 и x2 поменялись ролями. Точно так же при переходе от А к D поменяются ролями переменные x3 и y1.

Таким образом, чтобы перейти от некоторой вершины к какой-то соседней вершине, надо одну из базисных переменных сделать внебазисной и одну из внебазисных – базисной. Это значит, что при переходе от некоторой вершины к соседней надо одну из переменных, которой приписывалось значение нуль, сделать отличной от нуля и придать ей такое значение, чтобы другая переменная, значение которой ранее не было равным нулю, стало равным нулю. Это обстоятельство можно пояснить еще следующим образом. Пусть мы находимся в вершине А (см.

рис. 6.22), для которой x2=0; x3=0; y3=0. Чтобы перейти в соседнюю вершину D, будем двигаться по ребру AD, для которого x2 и y3=0, но x3 ≠ 0. Это движение по ребру AD надо совершать до тех

86

пор, пока значение переменной y1, отличное от нуля в вершине А, не станет равным нулю; тогда попадем в верхнюю грань и, следовательно, в вершину D.

Изложенные геометрические соображения лежат в основе той вычислительной процедуры, которая называется симплексным методом решения задачи линейного программирования.

Теперь становится ясным, что для проведения необходимых вычислений при рассмотрении какой-то вершины надо иметь алгебраические зависимости, которые выражают базисные переменные через небазисные. Точно так же для того, чтобы определить, достигнуто ли значение оптимума в рассматриваемой вершине, и если нет, то в какую соседнюю вершину следует перейти, чтобы улучшить достигнутый результат, надо иметь алгебраическое выражение для целевой функции Z через внебазисные переменные. Надо также уметь переходить от выражения для целевой функции Z и для базисных переменных через какой-то набор базисных переменных (определяющих некоторую вершину) к таким же выражениям через новые базисные переменные, набор которых соответствует соседней вершине. Для всего этого существует простой алгебраический аппарат (который укладывается в удобные для вычислений таблицы), называемый

жордановыми исключениями.

4.6.3.2. Жордановы исключения

Начнем с примера. Пусть даны линейные зависимости, выражающие переменные y1, y2, y3, Z через переменные x1, x2:

Можно трактовать эти соотношения как появившиеся в результате задания трех ограничений и целевой функции Z некоторой задачи линейного программирования. Считая x1 и x2 базисными переменными, y1, y2, y3 – внебазисными, можно также считать, что этими соотношениями заданы выражения внебазисных переменных и целевой функции через базисные переменные x1 и x2. Допустим, что мы хотим поменять ролями переменные x1 и y3, т.е. сделать y3 базисной, а x1 – внебазисной переменной. Как теперь будут выражаться внебазисные переменные y1, y2, x1 и целевая функция Z через новые базисные переменные y3 и x2? Для решения этой алгебраической задачи достаточно из третьего уравнения (4) y3=-2x1-x2+11 выразить x1 через y3 и x2 (что даст x1=-y3/2-x2/2+11/2) и полученное выражение для x1 подставить в выражения для остальных переменных y1, y2, Z. Сделав это, будем иметь:

Для удобства вычислений сделаем некоторые алгебраические преобразования. Перепишем соотношения (4) и (5) в виде зависимостей через «минус-базисные» переменные, т.е. зависимости

(4) запишем не через x1, x2, а через -x1, -x2 и зависимости (5) не через y3, x2, а через -y3, -x2. Получим:

87

Теперь запишем эти две системы зависимостей в виде двух таблиц, в которых сбоку помещены внебазисные переменные и целевая функция, а сверху – «минус-базисные» переменные

Таблица 1

Чем отличается табл. 1 от табл. 2? Прежде всего, следует заметить, что все элементы второй таблицы содержат в знаменателе число 2. Это не случайно. Дело в том, что число 2, выделенное в табл. 1, расположено на пересечении столбца для переменной -x1 и строки для переменной y3, т.е. на пересечении как раз того столбца и той строки, которые относятся к переменным, меняющимся ролями. Этот элемент называется ведущим при переходе от табл. 1 к табл. 2. Далее, назовем строку для y3 ведущей строкой, а столбец для x1 – ведущим столбцом (ведущий элемент стоит на пересечении ведущей строки и ведущего столбца).

Обнаруживаются такие три закономерности, относящиеся к ведущему столбцу и ведущей строке и имеющие место при переходе от табл. 1 к табл. 2:

1)ведущий элемент заменяется на обратное число;

2)остальные элементы ведущей строки делятся на ведущий элемент;

3)остальные элементы ведущего столбца также делятся на ведущий элемент и меняют знак.

Что касается закономерностей, которые относятся к прочим элементам (не расположенным в ведущей строке и ведущем столбце), то их обнаружить на числовом примере трудно. Поэтому проделаем необходимые преобразования в общем виде; при этом подтвердятся уже подмеченные правила и обнаружится правило для подсчета элементов, не расположенных в ведущих строке и столбце.

88

Пусть заданы линейные выражения переменных y1, y2,…, yr,…, ym, Z через

-x1, -x2,…, -xs,…, -xn:

y1 = a11 (−x1 ) + a12 (−x2 ) +... + a1s (−xs ) +... + a1n (−xn ) +b1; y2 = a21 (−x1 ) + a22 (−x2 ) +... + a2s (−xs ) +... + a2n (−xn ) +b2 ;

............................................................................

yr = ar1 (−x1 ) + ar 2 (−x2 ) +... + ars (−xs ) +... + arn (−xn ) +br ;

.............................................................................

Допустим, что нужно поменять ролями переменные xs и xr. Необходимые для этого алгебраические преобразования и составляют так называемый один шаг жордановых исключений сведущим элементом ars. Предполагая, что ведущий элемент ars ≠ 0, найдем сначала из r-го равенства (yr=…) выражение для xs:

Коэффициенты полученного выражения для xs составят элементы, расположенные в новой таблице вместо элементов ведущей строки старой таблицы. Заметим, что подтверждаются закономерности, 1 и 2, указанные выше.

Затем, подставив полученное выражение для xs в выражение для любого yi (i=1, 2,…, m; i ≠ r), получим:

где (как легко подсчитать)

Точно так же, подставив выражение для xs в выражение для Z, получим:

где

γ1' =γ1 − aar1rsγ s ;

γ2' =γ2 − aar1rsγ s ;

Запишем преобразованные выражения в табл. 4

Таблица 4

90

На основании формул (7) и (9) получаем простое правило перехода от табл. 3 к табл. 4:

1)ведущий элемент ars заменяется на обратное число 1/ars;

2)остальные элементы ведущей строки делятся на ведущий элемент;

3)остальные элементы ведущего столбца меняют знак и также делятся на ведущий элемент;

4)все прочие элементы получаются по правилу прямоугольника, которое заключается в следующем. Наметим мысленно в табл. 3 прямоугольник, у которого по диагонали расположены преобразуемый элемент, например, aij, и ведущий элемент ars (табл. 5). Преобразованный элемент aij' получится из преобразуемого элемента aij, если из него надо

вычесть частное от деления произведения элементов второй диагонали намеченного прямоугольника (arj, ais) на ведущий элемент (ars).

Таблица 5

Пример. Применим изложенное правило для перехода от табл. 1 к табл. 2 уже рассмотренного в начале этого раздела примера.

Что касается первых трех пунктов правила, то мы уже видели, что они подтверждаются. Рассмотрим теперь элементы, не расположенные в ведущих строке и столбце. Возьмем второй и третий элементы первой строки. Получим:

Возьмем второй и третий элементы последней строки. Получим: