
корнюшин.численные методы
.pdf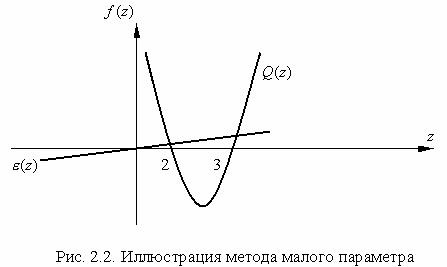
21
Пусть P(z) = 0 можно представить в виде
P(z) = Q(z) + ε(z), где ε(z) << Q(z)
Q(z) известны. Тогда корни P(z)
0,001x3 + x2 − 5x + 6 = 0
Обозначив Q(x) = x2 − 5x + 6,ε(x) = 0,001x3 , получим (как следует из анализа рисунка 2.2) небольшой сдвиг корней.
2.2.2. Вычисление значений корня с заданной точностью. Метод итераций
Будем считать, что первая задача (задача отделения корней) решена, т.е. выделена область, в которой P(z) = 0. Требуется найти в ней корень с любой точностью. Уравнение преобразуем к виду
z =ϕ(z), |
(1) |
например, с помощью следующего приема: |
|
z = z + cP(z), |
c = const ≠ 0. |
В выделенной области назначим приближение z0 – нулевое приближение корня. Следующие приближения корня находим так:
z1 =ϕ(z0 ), z2 =ϕ(z1 ),..., |
zn |
=ϕ(zn−1 ). |
(2) |
||
Предположим, что последовательность {z |
n |
}∞ |
сходится к некоторому z* , и что функция |
||
ϕ(z) непрерывна. Перейдем в (2) к пределу: |
|
n=0 |
|
|
|
|
|
|
|
|
|
z* = lim zn |
= limϕ(zn−1 ) =ϕ(lim zn−1 ) =ϕ(z* ). |
|
n→∞ |
n→∞ |
n→∞ |
Если указанный итерационный процесс сходится, то предел последовательности является |
||
решением исходного уравнения. |
|
|
При рассмотрении задачи в комплексной плоскости областью отделения корня является |
||
круг радиуса δ, а zo – центром этого круга. |
|
|
Теорема. Пусть уравнение z =ϕ(z) |
и радиус области отделения корня δ удовлетворяют |
|
следующим условиям: |
|
|
1) для любых двух точек z' и z' ' , находящихся в области| z − z0 |≤δ, имеет место неравенство
| ϕ(z' ) −ϕ(z' ' ) |≤ q | z'−z' '|,
22
где q – вещественное число из интервала (0,1); 2) имеет место неравенство
m |
≤δ, где m =| z0 −ϕ(z0 ) | . |
|
1 − q |
||
|
Тогда последовательность приближенных значений корня {zn } сходится, и предел
последовательности принадлежит заданной области отделения корня. Кроме того, скорость сходимости определяется следующим неравенством:
| zn − z |
* |
|≤ |
mq n |
. |
|
1 − q |
|||
|
|
|
|
Доказательство
Формально доказательство сводится к доказательству справедливости следующей формулы:
| zk − zk −1 |≤ mq k −1 для любого k =1,2,....
Проведем доказательство по индукции.
1. База индукции. Покажем, что формула справедлива при k =1: | z1 − z0 |=| ϕ(z0 ) − z0 |= m.
|
|
|
2. |
Индукционный шаг. Пусть формула верна для k = n. |
|
Докажем, что она верна для |
|||||||||||||||||||||
k = n +1, |
т.е. | zn+1 − zn |≤ mq n . Из справедливости формул для |
|
k =1,2,..., n |
|
следует, |
что все |
|||||||||||||||||||||
{zk }kn=1 |
находятся в круге выделения корня. Докажем это для любого k , например, для k = n : |
||||||||||||||||||||||||||
|
|
|
|
|
|
| zn − z0 |=| zn |
− zn−1 + zn−1 − zn−2 |
+ zn−2 −... − z1 |
|
+ z1 − z0 |≤ |
|
|
|
|
|||||||||||||
|
|
|
≤| zn − zn−1 | +| zn−1 − zn−2 | +...+| z1 − z0 |≤ mq n−1 |
+ mq n−2 +... + m ≤ m |
|
1 |
≤δ. |
|
|||||||||||||||||||
|
|
|
1 |
− q |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Итак, любая точка zk , k =1,2,..., n ,не выходит из круга выделения корня. Рассмотрим |
||||||||||||||||||||||||
|
|
|
| zn+1 − zn |=| ϕ(zn ) −ϕ(zn−1 ) |≤ q | zn − zn−1 |≤ mq n . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
k. |
Индукция закончена. Доказали, что неравенство | zk +1 − zk |
|≤ mq k |
справедливо при любых |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
{zk }∞k =0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Покажем теперь, что для последовательности |
выполняются |
необходимый и |
||||||||||||||||||||||
достаточный признаки Коши существования предела: ε > 0 N : n > N, p | zn+ p |
− zn |
|<ε, т.е. |
|||||||||||||||||||||||||
последовательность, сходящаяся в себе, сходится. Оценим разность |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
| zn+ p − zn |=| zn+ p − zn+ p−1 |
+ zn+ p−1 −... + zn+1 |
− zn |≤| zn+ p − zn+ p−1 | +...+| zn+1 |
− zn |
|≤ |
|||||||||||||||||||||
|
|
|
|
|
|
≤ m(q n+ p−1 + q n+ p−2 +... + q n ) ≤ |
|
m |
q n |
|
m |
|
|
q N |
≤ε . |
|
|
|
|
||||||||
|
|
|
|
1 − q |
1 |
− q |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Признак Коши выполняется, т.е. существует такая точка |
z* , |
что z* = lim zn . |
Т.к. все |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| z − z0 |≤δ, |
|
|
|
|
|
|
|
|
|
n→∞ |
|
|||
элементы последовательности принадлежат кругу |
|
то предел также лежит внутри |
|||||||||||||||||||||||||
этого круга. Докажем справедливость формулы скорости сходимости: |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
lim| zn+ p |
− zn |≤ lim |
m |
q n | zn − z* |≤ |
|
m |
|
q n . |
|
|
|
|
||||||||||
|
|
|
|
1 − q |
1 − q |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
p→∞ |
p→∞ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Покажем, что уравнение имеет единственное решение в круге радиуса δ. |
|
|
|
|||||||||||||||||||||
|
|
|
Проведем доказательство от противного. Пусть, кроме решения |
z* существует решение |
|||||||||||||||||||||||
|
|
≠ z* . |
Тогда | |
|
− z* |=| ϕ( |
|
) −ϕ(z* ) |≤ q | |
|
− z* |, |
|
|
|
|
|
противоречию, т.к. q <1. |
||||||||||||
|
z |
z |
z |
z |
|
что |
приводит |
|
к |
||||||||||||||||||
Итак, решение единственно. Обсудим условия теоремы.
При | z − z0 |≤δ | ϕ(z' ) −ϕ(z' ' ) |≤ q | z'−z' '| .
23
Это условие называется условием Липшица. Оно является более широким, чем условие дифференцируемости функций, т.е. функции, имеющие производную, входят в класс функций, удовлетворяющих условию Липшица. Если функция дифференцируема и ее производная ≤ q, то
она удовлетворяет условию Липшица. Действительно, применяя формулу Тейлора, можно записать
ϕ(z' ) −ϕ(z' ' ) =ϕ'[z'+Θ(z' '−z' )](z' '−z' ),0 < Θ <1,
или, переходя к модулю в левой и правой частях, и, обозначая максимум модуля производной через q, получаем условие Липшица.
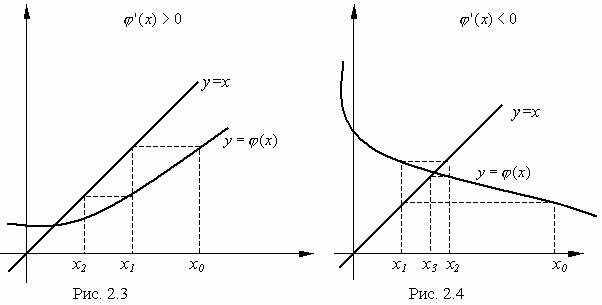
Качественно процесс нахождения корня методом итераций продемонстрирован на следующих рисунках 2.3 и 2.4, на которых представлены функции, имеющие соответственно положительное и отрицательное значения производных.
|
|
|
|
|
|
|
При ϕ' (x) > 0 последовательность x |
0 |
, x ,... монотонно сходится к корню x* , |
а при |
|
|
|
1 |
|
|
|
ϕ' (x) < 0 итерационный процесс "закручивается" вокруг корня x* . Корень находится |
между |
||||
двумя соседними значениями xk , xk +1 .
На рисунке 2.5 продемонстрировано, каким образом сказывается невыполнение условия Липшица.
24
Обсудим второе условие теоремы. Оно говорит о том, что разность | ϕ(x0 ) − x0 | не может быть сколь угодно велика: она ограничена величиной δ(1 − q). Скорость сходимости существенно зависит от величины q, что иллюстрируется следующими рисунками.
При q ≈ 0 итерационный процесс сходится к значению корня x* очень быстро, при q ≈1
– медленно.
2.2.3. Метод итераций для системы уравнений
Рассмотрим итерационный метод для решения системы k уравнений с k неизвестными:
|
|
|
|
|
|
|
|
25 |
P |
(ξ |
1 |
,ξ |
2 |
,...,ξ |
k |
) = 0, |
|
1 |
|
|
|
|
|
|||
P2 |
(ξ1 ,ξ2 |
,...,ξk |
) = 0, |
(3) |
||||
|
.................... |
|||||||
|
|
|||||||
P |
(ξ |
1 |
,ξ |
2 |
,...,ξ |
k |
) = 0. |
|
k |
|
|
|
|
|
|||
Преобразуем эту систему к виду, удобному для использования итерационного метода:
ξ1
ξ2
ξk
=ϕ1 (ξ1 ,ξ2 ,...,ξk ), |
|
|
=ϕ2 (ξ1 ,ξ2 ,...,ξk ), |
(4) |
|
.................... |
||
|
||
=ϕk (ξ1 ,ξ2 ,...,ξk ). |
|
Выбрав начальное приближение (ξ1(0) ,ξ2(0) ,...,ξk(0) соответствии с выражением
|
(1) |
=ϕ1 |
(0) |
(0) |
(0) |
), |
ξ1 |
(ξ1 |
,ξ2 |
,...,ξk |
|||
|
|
=ϕ2 |
(ξ1(0) ,ξ2(0) ,...,ξk(0) ), |
|||
ξ2(1) |
||||||
|
|
.......................... |
|
|||
|
|
|
||||
|
(1) |
|
(0) |
(0) |
(0) |
). |
ξk |
=ϕk (ξ1 |
,ξ2 |
,...,ξk |
|||
) , первое приближение будем искать в
(5)
Аналогично получаем следующие приближения.
Покажем, что, используя понятие функционального метрического пространства, можно данную задачу свести к задаче, рассмотренной в предыдущем разделе.
Пусть R – полное метрическое пространство, каждый элемент которого x задается
упорядоченным набором k чисел (действительных или комплексных) x(ξ1 ,ξ2 ,...,ξk ). |
Введем в |
||||||
пространстве |
метрику |
следующего |
вида: |
для |
любых |
двух |
элементов |
x' ={ξ1' ,ξ2' ,...,ξk' |
}, x' ' ={ξ1'' ,ξ2'' ,...,ξk'' }, пространства R |
|
|
|
|
||
|
|
ρ(x1 , x2 ) = max | ξ 'j' −ξ 'j | . |
|
(6) |
|
|
|
|
|
1≤ j≤k |
|
|
|
|
|
Эта метрика хороша тем, что дает максимальную "невязку" между левой и правой частями уравнения.
Введем вектор-функцию ϕ(x), являющуюся элементом пространства R. Координаты этой функции определятся следующим образом:
ϕ(x) ={ϕ1 (x),ϕ2 (x),...,ϕk (x)}, где ϕ j (x) =ϕ j (ξ1 ,ξ2 ,...,ξk ).
Используя введенное обозначение в метрическом пространстве, систему уравнений (4) можно переписать в следующем виде:
x =ϕ(x). |
(7) |
|
Зададим нулевое приближение x0 ={ξ1(0) ,ξ2(0) ,...,ξk(0) }, а также число δ > 0. |
||
Теорема. Пусть уравнение (7), нулевое приближение x0 |
и δ удовлетворяют следующим |
|
условиям: |
|
|
1) для любых x', x' ', принадлежащих области |
отделения |
корня радиуса δ, справедливо |
ρ(ϕ(x' ),ϕ(x' ' )) ≤ ρ(x', x' ' ), где 0<q<1;
2)имеет место неравенство m /(1 − q) ≤δ, где m = ρ(x0 ,ϕ(x0 )).
Тогда итерационный процесс вида xn =ϕ(xn−1 ) сходится, и lim{xn } является
единственным корнем уравнения (7) в заданном шаре. Обозначая этот предел через x*, можно утверждать, что скорость сходимости итерационного процесса определяется неравенством
ρ(xn , x* ) ≤ mq n /(1 − q).
Доказательство этой теоремы в точности повторяет доказательство предыдущей с заменой
| x'−x' '| на ρ(x', x' ' ).

26
2.2.4. Принцип сжатых отображений
Пусть R – полное метрическое пространство и пусть для всех элементов этого пространства определен оператор А "в себя" (результат действия этого оператора – отображение элементов в элементы того же пространства). Тогда говорят, что оператор А осуществляет сжатое отображение, если для любых двух элементов x', x'' этого пространства и любого действительного числа 0<q<1 имеет место неравенство
ρ(Ax', Ax' ' ) ≤ qρ(x', x' ' ),
т.е. образы элементов ближе, чем их прообразы. В таких случаях говорят, что оператор А сжимает. Теорема. Пусть в полном метрическом пространстве R оператор А осуществляет сжатие отображения "в себя". Тогда оператор А имеет единственную неподвижную точку, т.е. уравнение Ax=x имеет единственное решение, которое может быть получено как предел последовательности
итераций вида xn = Axn−1 (Точка является неподвижной для оператора, если он переводит ее саму
в себя).
Доказательство
Покажем, что последовательность значений {xn }∞n=0 , полученная итерированием,
сходится в себе, т.е. ρ(x |
, x |
m |
) →0. Будем считать n>m и запишем следующую |
n |
|
n,m→∞ |
последовательность неравенств:
ρ(xn , xm ) = ρ(Axn−1, Axm−1 ) ≤ qρ(xn−1, xm−1),
ρ(xn−1, xm−1 ) ≤ qρ(xn−2 , xm−2 ),
………………………………
ρ(xn−m+1, x1) ≤ qρ(xn−m , x0 ).
Перемножив эти неравенства, получим
ρ(xn , xm ) ≤ qm ρ(xn−m , x0 ).
Оценим ρ(xn−m , x0 ), применив n-m раз правило треугольника:
ρ(xn−m , x0 ) ≤ ρ(xn−m , xn−m−1 ) + ρ(xn−m−1, xn−m−2 ) +... + ρ(x1, x0 ) ≤
≤(qn−m−1 +... + q2 + q +1)ρ(x1, x0 ) < ρ1(x−1,qx0 ) .
Окончательно получаем
ρ(xn , xm ) ≤ 1q−mq ρ(x1, x0 ),
т.е. при n>m критерий Коши доказан: ρ(xn , xm ) →0. В силу полноты пространства R (для
n,m→∞
любой последовательности в пространстве R, сходящейся в себе, найдется предельный элемент,
принадлежащий этому пространству) существует такой элемент x*, что lim xn = x *. Используя то |
|||||||||||
обстоятельство, что оператор А – сжимающий, получим |
|
|
|
n→∞ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
n |
m |
ρ(Axn , Axm ) ≤ qρ(xn , xm ) |
|
n |
|
n |
|
n+1 |
|
||
n,m→∞ |
|
lim |
Ax |
= x |
, поэтому, |
||||||
и, следовательно, ρ(Ax , Ax ) →0, т.е. существует |
|
|
Ax . Но |
|
|
||||||
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
переходя в последнем равенстве к пределу, получаем |
Ax* = x* , |
т.е. x* – решение уравнения, а |
|||||||||
значит – неподвижная точка оператора. Покажем, что эта точка единственная. Проведем доказательство от противного. Предположим, что существует еще одна неподвижная точка x'≠ x* и Ax’=x’. Поскольку ρ(x* , x') = ρ(Ax* , Ax') ≤ qρ(x*, x'), а q<1, то получили противоречие, т.е. x’ не может быть неподвижной точкой.
27
2.2.5. Об одном принципе нахождения сходящихся итерационных процессов
Пусть имеется уравнение f (x) = 0, где x – действительная переменная и пусть на [a,b] отделен единственный корень x* этого уравнения. Пусть на этом сегменте задана некоторая непрерывная функция ψ(x). Тогда уравнение вида x = x −ψ(x) f (x) также имеет корень x*.
Принцип получения сходящихся итерационных процессов состоит в следующем. Нужно уметь так подобрать непрерывную функцию ψ(x), чтобы получившееся уравнение x = ϕ(x), где
ϕ(x) = x −ψ(x), давало сходящийся итерационный процесс.
2.2.6. Метод хорд (секущих) и метод деления пополам
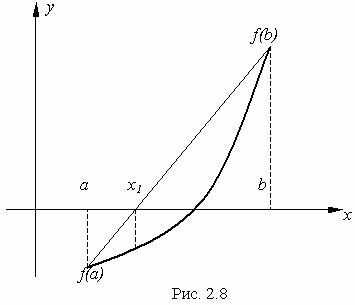
Данный метод является одним из методов, реализующих принцип получения сходящегося итерационного процесса. Пусть единственный корень x* уравнения f (x) = 0 отделен на [a,b].
Предположим, что f (x) изменяется на [a,b] монотонно.
Заменим кривую y = f (x) хордой, проходящей через точки (a, f (a)) и (b, f (b)). В качестве первого приближения корня уравнения f (x) = 0 возьмем точку пересечения этой хорды
с осью x. Запишем уравнение этой хорды: |
|
|
|
|
|
|
|
|
|
|||
|
|
|
y − f (a) |
|
= |
|
x − a |
, |
|
|||
|
|
|
f (b) − f (a) |
|
|
|||||||
|
|
|
|
|
b − a |
|
||||||
откуда получаем |
f (b) − f (a) |
|
|
|
|
|
|
|
||||
y = |
|
(x − a) + f (a). |
|
|||||||||
|
|
b − a |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
Подставляя в последнем выражении x = x1, y = 0, получаем |
|
|||||||||||
x |
= a − |
|
b − a |
|
f (a). |
|
||||||
|
|
|
|
|
|
|
||||||
1 |
|
|
|
|
f (b) |
− f (a) |
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
Полагая теперь x0 = a и учитывая, что f (xi ) < 0, f (b) > 0, имеем |
||||||||||||
xn = xn−1 − |
|
b |
− xn−1 |
|
|
|
f (xn−1 ). |
(8) |
||||
|
f (b) |
− f (xn−1 ) |
||||||||||
|
|
|
|
|
|
|
||||||
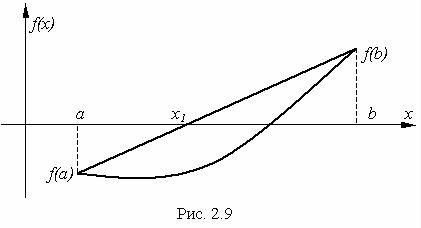
28
|
|
Теперь ясно, что роль функции ψ(x) выполняет выражение |
b − x |
. Надо доказать, |
||||||||||||||||||
|
|
f (b) − f (x) |
||||||||||||||||||||
что |
ψ(x) |
|
– |
сжимающий |
|
оператор. |
|
Возьмем |
|
для |
определенности |
|||||||||||
|
f (a) < 0, f (b) > 0, f ' (x) > 0, f ' ' (x) > 0. |
Этим |
|
знакам |
|
соответствует |
чертеж (рис. 2.8). Для |
|||||||||||||||
сходимости последовательности |
{xn |
}, значения элементов которой даются соотношением (8), |
||||||||||||||||||||
важно, |
что все |
эти |
значения |
ограничены |
по величине |
и |
не |
превосходят |
b. Т.к. |
|||||||||||||
|
b − xn−1 |
f (xn−1 ) < 0, то последовательность {xn} по признаку Вейерштрасса имеет предел |
||||||||||||||||||||
|
f (b) − f (xn−1 ) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
lim xn |
|
|
|
|
|
|
|
|
||||
(как монотонно возрастающая и ограниченная) |
= x* . Выясним, |
является ли этот предел |
||||||||||||||||||||
|
|
|
|
|
f (x) = 0 ? |
|
|
|
|
|
|
|
n→∞ |
|
|
|
|
|
|
|
n → ∞ : |
|
корнем |
уравнения |
С |
|
этой |
|
целью перейдем |
в |
(8) |
к |
пределу при |
||||||||||||
|
x* = x* − |
b − x* |
|
f (x* ). Поскольку |
|
|
b − x* |
|
≠ 0, |
то |
f (x* ) = 0, |
т.е. x* |
является |
|||||||||
|
f (b) − f (x* ) |
|
f (b) − f (x* ) |
|||||||||||||||||||
корнем |
уравнения |
f (x) = 0. |
При |
других |
соотношениях |
знаков |
f (a), f (b), f ' (x), f ' ' (x) |
|||||||||||||||
доказательство аналогично. |
|
(приближенным значением корня) и истинным значением x* , |
||||||||||||||||||||
|
|
Оценим разность между xn |
||||||||||||||||||||
полагая при этом, что f ' (x) сохраняет постоянный знак на [a,b]. По формуле Лагранжа |
|
|||||||||||||||||||||
|
|
|
|
f (xn ) − f (x* ) = f ' (ξ)(xn |
− x* ), |
где xn |
≤ξ ≤ x* |
или xn ≥ξ ≥ x* . |
|
|||||||||||||
|
|
Учитывая, что f (x* ) = 0 |
и полагая |
f ' (ξ) ≥ m = min | |
f ' (x) |, получаем оценку |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x [a,b] |
|
|
|
|
|
|
|
| xn − x* |≤ f (xn ) / m.
Формула тем точнее, чем меньше сегмент [a,b] отделения корня.
Из геометрии задачи вытекает, что первое приближение значения корня x1 делит сегмент [a,b] в соответствии со следующим соотношением:
x1 −a |
= |
| f (a) | |
, |
b − x |
| f (b) | |
||
1 |
|
|
|
в силу чего метод хорд часто называют методом пропорциональных частей. Если метод хорд "угрубить" и делить отрезок не на пропорциональные, а на две равные части, то получим метод нахождения корня делением сегмента пополам. При этом каждый раз после деления в качестве рабочей части выбирается та ее половина, на границах которой f(x) имеет противоположные знаки. Теоретическим основанием для сходимости этого метода служит лемма о вложенных интервалах. Каждый интервал содержится в другом, и при достаточно большом числе делений их длины стремятся к нулю. Тогда найдется только одна точка, которая принадлежит всем интервалам.
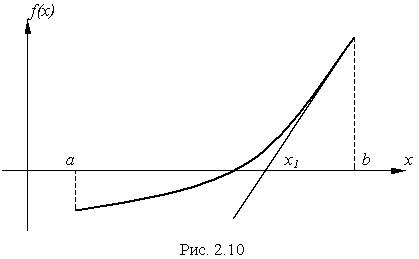
29
2.2.7. Метод Ньютона (метод касательных)
Пусть функция f(x) имеет на [a,b] единственный корень, и значения f(a), f(b) – противоположных знаков, существуют непрерывные f'(x), f''(x), которые сохраняют знак на [a,b].
Пусть некоторое значение x0 (a, b). Заменим f(x) некоторой линейной функцией, используя
формулу Лагранжа:
f (x) = f (x0 ) + f ' (ξ)(x − x0 ), где x <ξ < x0 x0 <ξ < x.
Поскольку значение ξ неизвестно, выберем в качестве ξ точку x0:
f (x) ≈ f (x0 ) + f ' (x0 )(x − x0 ). |
(9) |
Исходя из последнего соотношения, интересующее |
нас уравнение f(x)=0 заменим |
уравнением f(x0)+f'(x0)(x-x0)=0, корень которого примем за первое приближение значения корня уравнения f(x)=0:
x = x |
|
− |
1 |
f (x |
|
). |
(10) |
0 |
|
0 |
|||||
1 |
|
f ' (x0 ) |
|
|
|
||
|
|
|
|
|
|
|
Обобщая уравнение (10), получаем следующий итерационный процесс:
xn = xn−1 − |
1 |
f (xn−1 ). |
(11) |
|
|
f ' (xn−1 ) |
x = x −ψ(x) f (x) |
|
|||
|
|
|
|
||
Получили частный случай |
итерационного |
процесса |
при |
||
ψ(x) =1/ f ' (x) .
Сдругой стороны, уравнение (9) является уравнением касательной к кривой в точке x0. На каждом шаге итерационного процесса функция f(x) заменяется касательной к этой функции, проведенной в точке предыдущего приближенного значения корня. Из геометрии задачи вытекает,
что первую касательную удобно проводить с того конца сегмента, в котором выполняется условие f (x) f ' ' (x) > 0.
Теорема. Если функция f(x) имеет единственный корень на [a,b], непрерывные f'(x), f''(x), которые не меняют знака на этом сегменте, то если начинать итерационный процесс со значения
x0 [a, b], для которого выполняется условие f (x0 ) f ' ' (x0 ) > 0, то итерационный процесс
монотонно сходится к некоторому значению корня x*.
Рассмотрим упрощенный метод Ньютона. Он заключается в том, что итерационный процесс строится на основе следующей формулы:
xn = xn−1 + f (xn−1 ) / f ' (x0 ), |
(12) |
т.е. на каждом шаге используется одно и то же значение производной в начальной точке x0, что упрощает вычисления, но несколько уменьшает скорость сходимости итерационного процесса.
30
2.2.8. Вычисление значений алгебраического полинома
Пусть задан алгебраический полином n-й степени с действительными коэффициентами
P (x) = a |
0 |
x n +a |
x n−1 +... +a |
n−1 |
x +a |
n. |
(13) |
n |
1 |
|
|
|
Требуется определить значение этого полинома в точке x0. Подсчитаем число операций, необходимых для решения этой задачи. Операций умножения: n+(n-1)+(n-2)+…+1=n(n+1)/2; операций сложения: n. Нельзя ли предложить метод, сокращающий число операций? Рациональный процесс подсчета значения многочлена основан на теореме Безу.
Теорема. Остаток от деления многочлена Pn (x) на двучлен (x-x0) равен значению
многочлена в точке x0.
Доказательство
Запишем результат деления Pn (x) на (x − x0 ) в виде суммы остатка от деления R и
многочлена (n-1)-й степени Qn−1 (x), т.е. |
|
Pn (x) = (x − x0 )Qn−1 (x) + R.. |
(14) |
Положим в этом выражении x=x0:
Pn (x0 ) = (x0 − x0 )Qn−1 (x0 ) + R = R. .
Вычислим Qn−1 (x) : |
|
|
|
|
|
|
|
|
|
Q |
n−1 |
(x) = b |
0 |
x n=1 +b x n−2 |
+... +b |
n−2 |
x +b |
n−1 |
. (15) |
|
|
1 |
|
|
|
||||
Подставив этот результат в (14), получим
Pn (x) = (x − x0 )(b0 x n−1 +b1 x n−2 +... +bn−2 x +bn−1 ) + R..
Выразим коэффициенты многочлена Qn-1 через коэффициенты Pn.
Теорема. Два многочлена тождественно равны тогда и только тогда, когда их коэффициенты при одинаковых степенях x совпадают.
Имеем:
a0 = b0 , a1 = b1 −b0 x0 , a2 = b2 −b1 x0 ,..., ak = bk −bk −1 x0 ,..., an = bn −bn−1 x0 |
, откуда |
b0 = a0 , b1 = a1 +b0 x0 , b2 = a2 +b1 x0 ,..., bk = ak +bk −1 x0 ,..., bn = an +bn |
−1 x0 . |
Преобразование коэффициентов удобно представить в виде так называемой схемы Горнера (таблица 1).
Таблица 1
|
|
a0 |
|
a1 |
|
a2 |
|
… |
ak |
… |
|
an |
|
|
|
|
|
b0x0 |
|
b1x0 |
|
… |
bk-1 x0 |
… |
|
bn-1x0 |
|
|
x0 |
b0 |
|
b1 |
|
b2 |
|
… |
bk |
… |
|
bn |
|
В соответствии |
с теоремой |
Безу |
bn = R = Pn (x0 ). При |
этом |
выполнено n действий |
||||||||
умножения и n действий сложения.
Пример. P(x) = 3x5 −4x 4 +2x 2 |
− x +10, P(2) −? |
|
|
|||||
Таблица 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
-4 |
|
0 |
2 |
-1 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
4 |
8 |
20 |
38 |
|
|
|
|
|
|
|
|
|
|
2 |
3 |
2 |
|
4 |
10 |
19 |
48 |
|
|
|
|
|
|
|
|
|
