корнюшин.численные методы

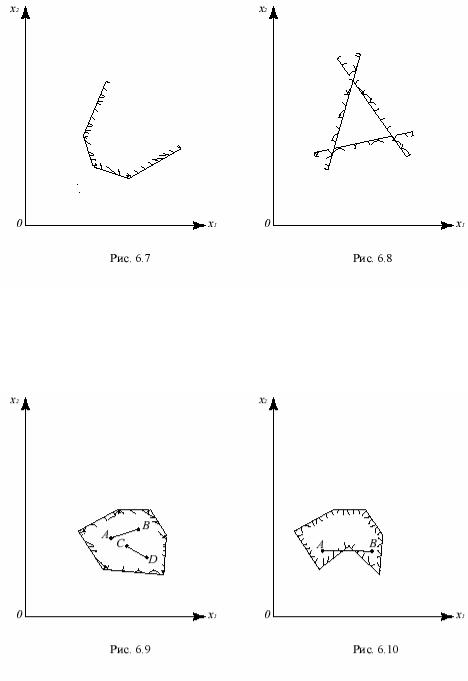
71

В теории линейного программирования доказывается, что многоугольная область, изображающая систему ограничений, всегда является выпуклой, т.е. такой, которая вместе с любыми двумя точками содержит и весь отрезок, их соединяющий (рис.6.9), а не такой, какая изображена на рис.6.10.

4.6.2.2. Геометрический смысл задачи линейного программирования

Теперь рассмотрим целевую функцию

Z=c1x1+c2x2.

Если приравнять Z какой-нибудь постоянной величине, т.е. рассмотреть те планы x1, x2, при которых целевая функция сохраняет одно и то же значение Z=const, то получим прямую линию (l), которая называется линией уровня функции Z=c1x1+c2x2:

с1x1+c2x2=const.

Если значение этой константы будем увеличивать (или уменьшать), то прямая (l) будет перемещаться параллельно самой себе (и в каком-то определенном направлении), т.к. у прямых c1x1+c2x2=l1 и c1x1+c2x2=l2 один и тот же угловой коэффициент k=-c1/c2.

Как узнать, в каком направлении надо передвигать прямую (l), изображающую линию уровня целевой функции, чтобы значение Z увеличивалось (или уменьшалось)? Для этого

72

достаточно зафиксировать значение константы в уравнении Z=const (c1x1+c2x2=const). Тогда получится какая-то определенная прямая (l), и, чтобы ответить на поставленный вопрос, достаточно по предыдущему правилу узнать, с какой стороны от прямой (l) значение целевой функции Z=c1x1+c2x2 больше фиксированной константы, поставленной в правую часть уравнения c1x1+c2x2=const.

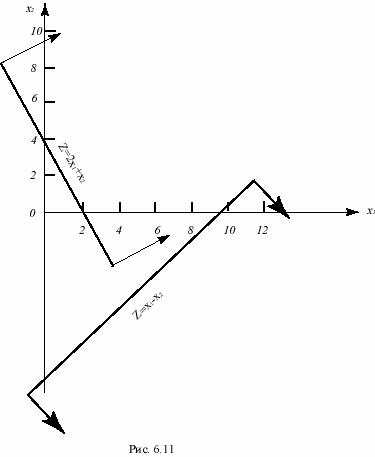
Например, значение целевой функции Z=2x1+x2 увеличивается при движении, показанном на рис.6.11 стрелками около прямой 2x1+x2=4. На том же рисунке показано, в какую сторону увеличивается значение целевой функции Z=x1–x2.

Теперь дадим окончательное геометрическое истолкование задачи линейного программирования и одновременно получим графический способ ее решения (для случая двух переменных).

Пусть дана задача линейного программирования (например, на максимум)

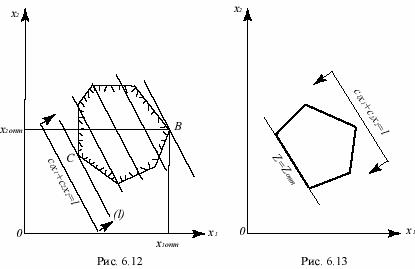
Прежде всего, можно построить многоугольник ограничений (2). Как уже отмечалось, он будет выпуклым (рис.6.12) и, в силу требований (3), расположен в первом квадранте.

73

После этого проведем какую-нибудь определенную линию уровня Z=const целевой функции, например, прямую c1x1+c2x2=l и покажем стрелками, куда ее надо двигать, чтобы целевая функция увеличивала свое значение. Очевидно, что искомый оптимум найдется, когда прямая (l), двигаясь к границе многоугольника ограничений, покинет этот многоугольник – это произойдет в некоторой вершине многоугольника ограничений. Определив координаты x1B и x2B вершины B, найдем оптимальный план: x1опт=x1В, x2опт=x2В. Вычислив затем значение целевой функции в вершине B, найдем искомый оптимум:

Zmax=c1x1B+c2x2B.

Если бы при тех же ограничениях была поставлена задача на минимум, то ясно, что линию уровня целевой функции – прямую (l) – надо двигать в противоположную сторону, и мы получим минимум в некоторой вершине C многоугольника ограничений.

Это свойство является общим: оптимальное значение целевой функции, если оно существует, всегда достигается в некоторой вершине многоугольника ограничений.

Если область, задаваемая ограничениями, бесконечна (см. рис.6.7), то один из оптимумов (максимум или минимум) может стать бесконечным, но другой по-прежнему достигается в некоторой вершине. Может, однако, случиться что линия уровня целевой функции – прямая (l) – окажется параллельной какому-то звену многоугольника ограничений (рис.6.13). В этом случае (при отыскании одного из оптимумов – максимума или минимума) прямая (l), покидая многоугольник ограничений, ляжет на параллельное ей звено, и координаты любой точки этого звена дадут оптимальный план, так что оптимальных планов будет бесконечное множество. Но для любого из них целевая функция имеет одно и то же значение (т.к. точки лежат на одной и той же линии уровня), поэтому оптимум, конечно, будет один. В этом случае говорят, что имеются

альтернативные оптимальные планы.

4.6.2.3. Задачи

Рассмотрим несколько задач для иллюстрации графического метода. Первая из них – численный пример, а остальные имеют экономическое содержание.

Задача 1. Найти максимум функции Z=x1–5x2 при ограничениях

− x1 + 2x2 ≤ 5; x1 + x2 ≤ 7; 2x1 + x2 ≤11; x1 + 2x2 ≥ 7; x1 ≥ 0; x2 ≥ 0.

Решение. Построим прямые

74

(l1 ) : −x1 + 2x2 = 5; (l2 ) : x1 + x2 = 7; (l3 ) : 2x1 + x2 =11; (l4 ) : x1 + 2x2 = 7

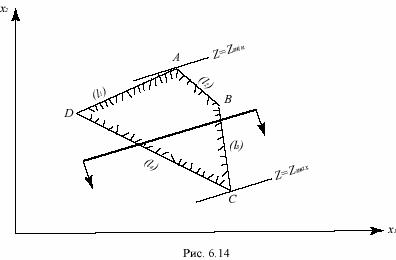
и определим общую часть полуплоскостей, изображающих неравенства-ограничения задачи (рис.6.14). Тогда определится многоугольник ограничений ABCD.

Затем построим какую-нибудь определенную линию уровня целевой функции, например, прямую (l) и узнаем, в какую сторону ее надо параллельно перемещать, чтобы значение целевой функции Z увеличивалось (показано стрелками около прямой (l)). Очевидно, Zmax достигается в вершине C – точке пересечения прямых (l3) и (l4), соответствующих уравнениям

2x1+x2=11;

x1+2x2=7.

Решая эти уравнения, находим x1опт=5, x2опт=1 и, следовательно, Zтах=x1опт–5x2опт =5- 5*1=0. Если бы при тех же ограничениях была поставлена задача на минимум (Z=x1-5x2 → min),

то, двигая прямую (l) в сторону, противоположную стрелкам, мы получили бы оптимальный план в вершине A – точке пересечения сторон (l1) и (l2), соответствующих уравнениям

-x1+2x2=5;

x1+x2=7.

Решая эти уравнения, находим оптимальный план на минимум: x’1опт=3, x’2опт=4 и,

следовательно, Zmin=x’1опт–5x’2опт=3-5*4=-17.

Задача 2. Для осуществления буксирно-биржевых перевозок на двух линиях А и В портовый флот располагает определенным числом барж четырех типов. По условиям эксплуатации буксирный воз для каждой линии должен состоять из определенного набора барж разных типов. Требуется распределить имеющиеся баржи по линиям А и В так, чтобы общая грузоподъемность возов была наибольшей. Исходные данные указаны в табл.1.

Таблица 1

75

Решение. Из условия задачи получаем, что грузоподъемность одного буксирного воза на линии А составляет 2*300+1*500+4*600+0*800=3500 т, а на линии В она равна 4800 т. Если запланировать x1 возов на линию А и x2 возов на линию В, то добьемся общей грузоподъемности

Z=3500x1+4800x2 т.

Это – целевая функция, которую нужно максимизировать. Но имеются ограничения по числу барж каждого типа (последний столбец табл.1), и эти ограничения записываются в виде неравенств

(I ) : 2x1 + 2x2 ≤ 20; (II ) : x1 + 2x2 ≤14; (III ) : 4x1 +0x2 ≤ 32; (IV ) : 0x1 + 4x2 ≤ 24.

Кроме того, естественно, что x1 ≥ 0, x2 ≥ 0 .

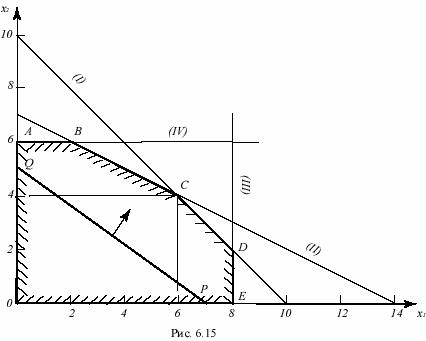
Мы получили задачу линейного программирования, которую будем решать графически. Изобразив полуплоскости, ограниченные осями координат x1, x2 и прямыми (I), (II), (III), (IV) на рис 6.15, получаем многоугольник ограничений OABCDE.

Теперь изобразим какую-нибудь линию уровня Z=const целевой функции. Полагая, например, const=24000, получаем прямую 3500x1+4800x2=24000, которая пересекает оси координат в точках Р (ОР=24000/3500=6,83) и Q (OQ=24000/4800=5).

Для того чтобы значение Z увеличивалось, надо прямую PQ перемещать параллельно в сторону, указанную стрелкой. Очевидно, max Z достигается в вершине С с координатами x1опт=6, x2опт=4. Это и есть оптимальный план для числа возов на линиях А и В соответственно.

Следовательно, для достижения наибольшей общей грузоподъемности надо на линию А планировать 6 возов, а на линию В – 4 воза; при этом плане достигается Z =40200 т. Использование ресурсов (имеющихся в распоряжении барж) при этом оптимальном плане характеризуется следующими числами:

тип I: 2*6+2*4=20, т.е. 100%;

76

тип II: 1*6+2*4=14, т.е. 100%;

тип III: 4*6+0*4=24, т.е. 75%;

тип IV: 0*6+4*4=16, т.е. 66,7%.

Задача 3. Автосборочный завод, выпускающий как легковые, так и грузовые автомобили, имеет в своем составе четыре цеха: кузнечно-прессовый, цех двигателей, сборочный легковых машин и сборочный грузовых машин, производительности которых (за месяц) указаны в табл. 2. Прибыль предприятия (в ден. ед.) от реализации одной грузовой машины – 250, одной легковой –

300.

Таблица 2

Требуется составить месячный план выпуска легковых и грузовых машин, обеспечивающий достижение максимальной прибыли.

Решение. Если планировать месячный выпуск x1 грузовых и x2 легковых машин, то предприятие получит прибыль Z=250x1+300x2. Это – целевая функция, которую нужно максимизировать.

Ограниченные производственные мощности цехов приводят к неравенствам:

(l1 ) : 35x1 + 25x2 ≤1;

(l2 ) : 16x1,6 + 33x2 ≤1; (l3 ) : x1 ≤15;

(l4 ) : x2 ≤ 22,5.

Первое неравенство получено из таких соображений. Если кузнечно-прессовый цех выпускает x2 легковых машин в месяц, то он на это затрачивает такую долю своей месячной производительности, которая выражается дробью x2/25. Кроме того, цех работает на выпуск x1 грузовых машин и затрачивает на это еще такую долю своей месячной производительности, которая выражается дробью x1/35; сумма этих долей, очевидно, не превышает единицы. Из тех же соображений составлено второе неравенство. Третье и четвертое неравенства непосредственно вытекают из данных о производительности сборочных цехов. К этим неравенствам необходимо

присоединить условия неотрицательности: x1 ≥ 0, x2 ≥ 0

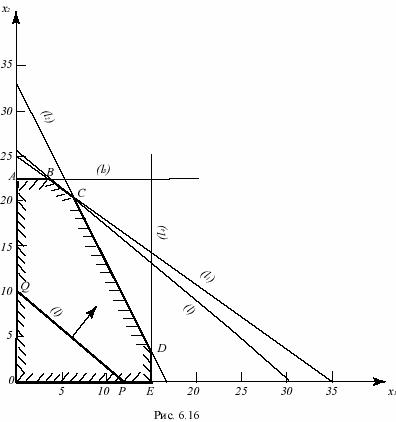
На рис.6.16 изображен многоугольник ограничений OABCDE.

77

Далее, рассмотрим прямую (l) – линию уровня Z=const целевой функции, полагая const=3000, т.е. прямую 250x1+300x2=3000 (она отсекает на осях отрезки OP=3000/250=12, OQ=3000/300=10, что соответствует месячному плану выпуска 12 тыс. грузовых или 10 тыс. легковых машин, при котором прибыль равна 3 млн. ден. ед.). Чтобы значение Z увеличивалось, надо прямую двигать в сторону, указанную стрелкой Оптимум достигается в вершине C, в которой пересекаются прямые (l1) и (l2). Из уравнений этих прямых (или из чертежа) находим координаты точки C: x2=20,5; x1=6,3. Следовательно, оптимальный план месячного выпуска будет такой: легковых машин – 20500 и грузовых – 6300. При этом достигается максимальная прибыль Zmax=7725000 ден. ед. Как легко подсчитать, использование производственных мощностей цехов при оптимальном плане следующее: кузнечно-прессовый – 100%, цех двигателей – 100%, сборочный легковых машин – 91%, сборочный грузовых машин – 42%.

Задача 4. На некотором направлении пароходство должно перевезти четыре груза в количествах, нижние пределы которых указаны в табл. 3. Для осуществления этих перевозок выделено два судна. Исходя из условий наилучшего использования грузоподъемности и грузовместимости и учитывая требования совместимости и грузовой специализации, каждое из выделенных судов может принять одновременно определенное количество каждого груза, указанное в таблице. Там же указаны эксплуатационные расходы выделенных судов (за рейс). Требуется составить план, обеспечивающий перевозку предъявленных грузов с наименьшими расходами.

Таблица 3

78

Решение. Если планировать для судна I x1 рейсов, а для судна II x2 рейсов, то суммарные расходы составят (в руб.) Z=12000x1+16000x2.

Это – целевая функция, которую надо минимизировать. При планируемом числе рейсов удастся перевезти (3000x1+3000x2) т груза А, (1000x1+2000x2) т груза Б, (0x1+4000x2) т груза В и (2000x1+0x2) т груза Г. Имея в виду указанные в таблице нижние пределы заданного объема перевозок по каждому грузу, получаем неравенства ограничения:

3000x1 +3000x2 ≥ 21000;

1000x1 + 2000x2 ≥10000;

4000x2 ≥ 4000;

2000x1 ≥ 4000.

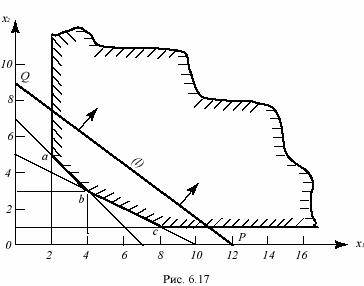
По этим неравенствам строим область ограничений (рис. 6.17), которая теперь является неограниченной областью (заштрихована).

Линия уровня Z=const целевой функции Z при const=144000 – это прямая, уравнение которой 12000x1+16000x2=144000. Эта прямая отсекает на осях отрезки OP=144000/12000=12; OQ=144000/16000=9. Ее надо двигать в сторону, противоположную направлению, указанному стрелками, т.к. решается задача на минимум.

Из рисунка видно, что минимум достигается в точке b, координаты которой дают оптимальный план x1опт=4; x2опт=3. Следовательно, для достижения минимальных эксплуатационных расходов надо планировать судну I 4 рейса, а судну II – 3 рейса. Расход при этом плане будет Z=12000*4+16000*3=96000 руб. Грузы будут перевезены в таких количествах (в

т):

груз А: 3000*4+3000*3=21000; груз Б: 1000*4+2000*3=10000; груз В: 4000*3=12000;

груз Г: 2000*4=8000,

т.е. грузы А и Б будут перевезены в количествах, указанных нижними пределами для них, а грузы В и Г будут перевезены в количествах, превосходящих нижние пределы на 8000 и 4000 соответственно.

Задача 5. За время Т=3 ед. (например, 3 мес.) необходимо перевезти на линии 1 18000 т, а на линии 2 – 48000 т грузов. Для этих перевозок можно использовать суда двух типов, для которых известны провозные способности и эксплуатационные расходы (табл. 4).

79

Таблица 4

Требуется составить план работы судов, обеспечивающий выполнение заданного объема перевозок в указанное время с минимальными эксплуатационными расходами.

Решение. В качестве параметров управления выберем время, назначенное судну каждого типа для работы на каждой из линий, так что намечаемый план работы судов будет состоять из следующих величин:

x11 – время работы судов 1 типа на линии 1;

x12 – то же, на линии 2;

x21 – время работы судов 2 типа на линии 1;

x22 – то же, на линии 2.

При таком плане эксплуатационные расходы составят сумму (в тыс. руб.)

Z=10x11+15x12+24x21+30x22, (4)

которая является целевой функцией задачи; ее надо минимизировать. Ограничения задачи запишутся в виде следующих соотношений:

16x12 +30x22 = 48,

где первые два выражают требования выполнить перевозки в заданное время, а последние два выражают требования выполнить заданный объем перевозок на каждой линии. К этим ограничениям добавляются требования неотрицательности:

Полученная задача линейного программирования отличается от предыдущих тем, что в ней 4 переменных, и для того чтобы можно было получить решение графически, надо свести ее к задаче с двумя переменными. Это можно сделать, выразив, например, из двух последних ограничений-равенств (5) переменные x21 и x22 через переменные x11 и 12:

и подставив эти выражения в целевую функцию (4), во второе неравенство и в последние два неравенства (6). Тогда после простейших вычислений получим задачу:

Z = 2x11 − x12 +96 → min;

x11 + x12 ≤ 3;

5x11 +8x12 ≥ 9;

x11 ≤ 6; x12 ≤ 3; x11 ≥ 0; x12 ≥ 0.

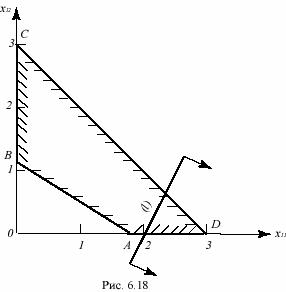
Если отложим на оси абсцисс величину x11, а на оси ординат x12 (рис.6.18), то эти ограничения приведет к многоугольнику ABCD (прямые x11=6 и x12=3 не входят в звенья этого

80

многоугольника, т.к. неравенства x11 ≤6 и x12 ≤3 являются следствиями неравенства x11+x12 ≤3 и условия неотрицательности).

Найдем какую-нибудь линию уровня Z=const целевой функции. Положим, например, const=100; тогда получим прямую (l), уравнение которой будет 2x11-x12=4 (эта прямая отсекает на осях отрезки x11=2; x12=-4). Т.к. мы ищем минимум, то прямую надо перемещать в сторону, противоположную направлению, указанному стрелками. Теперь ясно, что минимум достигается в вершине С, для которой x11=0, x12=3. Из равенств (7) имеем далее, что x21=2; x22=0. Таким образом, оптимальным будет план x11=0; x12=3; x21=2; x22=0; для этого плана расходы составят

Zmin=93 тыс. руб.

Использование судов в оптимальном плане следующее: суда первого типа используются в течение всего эксплуатационного периода, суда второго типа осваивают свое задание за 2 ед. времени и в оставшееся время (1 ед. времени) могут быть использованы для других перевозок.

4.6.2.4.Обобщение геометрической интерпретации на многомерный случай

Впредыдущих разделах была рассмотрена интерпретации задачи линейного программирования (и основанный на ней графический способ) для случая, когда число параметров

задачи равно двум (или сводится к двум). Если бы задача выражалась через три параметра x1, x2 и x3, ее геометрическое истолкование было бы подобно изложенному выше, со следующими изменениями в деталях:

1) всякое линейное уравнение a1x1+a2x2+a3x3=b изображается некоторой плоскостью в пространстве координатных осей x1, x2, x3 (рис.6.19);