корнюшин.численные методы

41

42

Модуль 3. Численное интегрирование и решение систем алгебраических уравнений

3.4.Численное интегрирование

3.4.1.Задача приближенного вычисления определенного интеграла

Пусть дан интеграл J = ∫ab f (x)dx , где a,b < ∞ . На практике часто встречаются

следующие ситуации, требующие применения численного интегрирования: для заданного интеграла не существует первообразной («не берущийся» интеграл); первообразная сложна, и ее вычисление связано со значительными трудностями. В качестве приближенных значений интегралов в этих случаях естественно воспользоваться оценками по формулам, напоминающим интегральные суммы, т.е. линейные комбинации конечного числа значений подынтегральной

b

функции на заданном сегменте: J = ∫a f (x)dx ∑nk =1 ck(n) f (xk(n) ) . Формулы такого типа называются квадратурными. Значения {xk(n) } называются узлами, а {ck(n) } – коэффициентами квадратурных формул. Число Rn ( f ) = ∫ab f (x)dx − ∑nk =1 ck(n) f (xk(n) ) называется остаточным

членом квадратурной формулы.

При такой постановке возникают две задачи: 1) нужно определить, каким образом разбивать сегмент [a,b], и как выбирать узлы, чтобы получить возможно более точное значение интеграла; 2) необходимо решить проблему увеличения скорости сходимости интегральных сумм.

Часто рассматривают вычисление интегралов более общего вида

a

где p(x) – весовая функция. Можно строить квадратурные формулы из разных соображений. Рассмотрим некоторые из них.

3.4.1.1. Квадратурные формулы с наилучшей точностью для данного класса функций

Обозначим через R некоторый класс функций, интегрируемых по Риману. Пусть

_

Rn = sup Rn ( f ) , где Rn(f) – остаточный член некоторой квадратурной формулы для функции

f R

f R . Ставится задача такого выбора узлов и коэффициентов квадратурной формулы, чтобы

_

величина Rn , т.е. точная верхняя грань по остаточным членам всех функций этого класса, была наименьшей. Такую формулу н6азывают формулой с наилучшей точностью для данного класса функций.

3.4.1.2. Квадратурные формулы с наилучшей степенью точности

Пусть {ϕk (x)}∞k =0 – базисное множество в некотором пространстве функций, причем

множество функций {ϕk (x)}nk =0 . Где n – фиксированное число, образует систему Чебышева порядка n (многочлен по этой системе имеет не более n корней). Обозначим через Фm(x) множество всех многочленов вида ∑mk =0αkϕk (x) , где α0, α1,…, αm – действительные числа.

43

Зафиксируем число узлов квадратурной формулы n и будем подбирать ее коэффициенты и расположение узлов так, чтобы эта формула была точна для многочленов как можно более высокой степени m. Порядок многочлена m, для которого формула еще точна (при условии, что она уже не точна для многочлена порядка m+1) и называется степенью точности квадратурной

функция f(x). Рассмотрим интеграл ∫ab p(x) f (x)dx и построим на [a,b] по узлам {x j }nj=0

интерполяционный полином Лагранжа Ln(x)= ∑nj=0 f (x j )Φ j (x). Поскольку f(x)=Ln(x)+Rn(x), то

b ∑n b b

∫a p(x) f (x)dx = j=0 f (x j )∫a p(x)Φ j (x)dx + ∫a p(x)Rn (x)dx =

= ∑nj=0 c(jn) f (x j ) + R( f ),

где c(jn) = ∫ab p(x)Φ j (x)dx (j=0, 1,…, n) – коэффициенты, а R( f ) = ∫ab p(x)Rn (x)dx – остаточный член квадратурной формулы интерполяционного типа. Коэффициенты c(jn) не зависят

от f(x), а определяются только весовой функцией и узлами интерполяции.

Установим связь между квадратурной формулой интерполяционного типа и квадратурными формулами определенного порядка точности по отношению к определенному виду многочлена.

Теорема. Необходимое и достаточное условие того, чтобы квадратурная формула с n узлами была интерполяционной для системы функций {ϕk (x)}nk−=10 , которая является системой Чебышева, заключается в следующем: эта формула должна иметь порядок точности не ниже n-1 для системы обобщенных многочленов вида ∑nj−=10α jϕ j (x) , где αj – любые действительные числа.

интерполяционной формулой. Следовательно, эта формула точна, если в качестве функции f(x) взять некоторый многочлен вида ∑nj−=10α jϕ j (x) . Действительно, функция совпадает со своим

интерполяционным многочленом, и остаточный член полинома Лагранжа равен нулю, а поэтому равен нулю и остаточный член квадратурной формулы.

Достаточность. Пусть квадратурная формула является точной по заданной системе функций для многочленов порядка не ниже n-1. В частности, эта формула будет точна для

Итак, коэффициенты данной квадратурной формулы выражаются как коэффициенты интерполяционной формулы. Следовательно, данная квадратурная формула является интерполяционной.

Следствие. Интерполяционная квадратурная формула с n узлами по системе функций {ϕk (x)}nk−=10 имеет порядок точности по этой системе функций не ниже, чем n-1.

45

Следствие. Из свойств коэффициентов Котеса вытекает, что эти формулы нецелесообразно применять при больших значениях n.

3.4.3. Частные случаи формулы Ньютона-Котеса

3.4.3.1. Формула прямоугольников

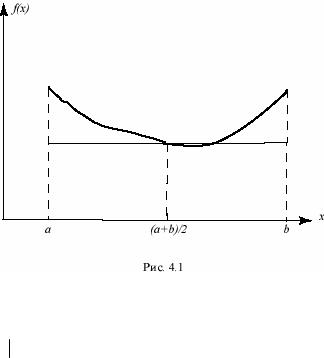
Рассмотрим формулу Ньютона-Котеса открытого типа с одним узлом. Эта формула верна для алгебраических многочленов нулевой степени. Выберем в качестве узла интерполяции середину заданного интервала интегрирования [a,b]. Тогда, применяя формулу Котеса, получаем соотношение, называемое формулой прямоугольников:

Это название следует из того, что искомое значение интеграла приближенно оценивается площадью прямоугольника, имеющего высоту, равную значению подынтегральной функции в точке (a+b)/2, а его длина равна длине отрезка [a,b] (см. рис. 4.1).

Если функция f(x) имеет ограниченную вторую производную, то для остаточного члена имеется следующая оценка:

На практике применяют обобщенную формулу прямоугольников. Она получается следующим образом. Отрезок интегрирования [a,b] разбивается на m равных частей и к каждому элементарному сегменту применяется формула прямоугольников:

3.4.3.2. Формула трапеций

Формула трапеций. Так называется формула Ньютона-Котеса замкнутого типа с двумя узлами. Интерполяционная формула точна для многочленов первой степени, т.е. для линейных функций. Запишем эту формулу с оценкой остаточного члена:

Аналогично предыдущему случаю разбив [a,b] на m частей и применив на каждой из них формулу трапеции, получим обобщенную формулу трапеции:

где введены следующие обозначения: yi=f(xi), i=0, 1,…, m.

3.4.3.3. Формула парабол (Симпсона)

Рассмотрим формулу Ньютона-Котеса замкнутого типа с тремя узлами. Эта формула является точной для любого многочлена степени не больше двух.

Построим функцию y=Ax2+Bx+C по трем равноотстоящим точкам (x=a, x=(a+b)/2, x=b), значения которой в этих точках равны значениям заданной функции y0, y1, y2. Сделав замену переменной t=x-(a+h/2), где h=b-a, получим следующую систему уравнений

Сложив уравнения этой системы, предварительно домножив второе уравнение на 4, получим следующее соотношение:

Ah2/2+6C=y0+4y1+y2. (9)

Вычислим

S = ∫h / 2 (Ax2 + Bx + C)dx = Ax3 / 3 h / 2 +Ch =Ah3 /12 +Ch = h( Ah2 / 2 + 6C) / 6 ,

−h / 2 −h / 2

или, с учетом (9) S=h(y0+4y1+y2)/6=(b-a)(y0+4y1+y2)/6. Если теперь подынтегральную функцию f(x) заменить функцией y, то получим в качестве частного случая формулы НьютонаКотеса формулу парабол (Симпсона):

Для остаточного члена в случае существования ограниченной четвертой производной функции f(x) справедлива следующая оценка:

Разделив далее отрезок на 2m частей, обозначая значения функции f(x) в точках деления yi, применяя к двум последовательным сегментам формулу Симпсона (всего m раз) и складывая, получим:

3.4.4. Квадратурные формулы Гаусса

Квадратурные формулы Гаусса. Такое название носят квадратурные формулы с наивысшим порядком точности относительно алгебраических многочленов. Пусть дан интеграл

47

∫ab p(x) f (x)dx . Требуется таким образом выбрать n узлов на [a,b] и n коэффициентов

квадратурной формулы, чтобы эта формула была точна для алгебраических многочленов как можно более высокой степени. Пусть формула точна для многочленов степени m: f(x)=a0+a1x+…+amxm. Тогда имеем

С другой стороны ∫ab p(x) f (x)dx = ∑nk =1 ck(n) f (xk ). Учитывая, что последняя формула по

предположению верна для любого многочлена степени m, т.е. для любых наборов коэффициентов a0, a1,…,am, в силу произвольности этих коэффициентов (полагая отличным от нуля только ai в i-м уравнении, а значения остальных m-1 коэффициентов в i-м уравнении принимая равными нулю) получим следующую систему уравнений

Введенная в системе уравнений величина, обозначенная µk, k=0, 1,…, m называется моментом функции p(x).

Поскольку имеется m+1 уравнение, а неизвестных 2n (n переменных и n коэффициентов), то из равенства m+1=2n следует максимальная степень многочлена, для которого квадратурная формула еще точна: m=2n-1.

Для доказательства существования решения системы уравнений (15) введем в

рассмотрение многочлен ωn(x) с единичным старшим коэффициентом, корнями которого являются искомые узлы: ωn(x)=(x-x1)(x-x2)…(x-xn).

Теорема. Необходимое и достаточное условие того, чтобы квадратурная формула с n узлами имела алгебраический порядок точности 2n-1 заключается в следующем: узлы этой функции должны быть корнями многочлена ωn(x), ортогонального с весом p(x) к любому многочлену степени не выше n-1, т.е. для любого многочлена q(x) степени не выше n-1 должно иметь место равенство

Доказательство.

Необходимость. Пусть формула является точной для любого многочлена степени не выше 2n-1. Требуется доказать, что имеет место равенство (16).

Учитывая, что степень q(x) не выше n-1, получаем, что ωn(x)q(x) имеет степень не выше, чем 2n-1. Следовательно, для многочлена ωn(x)q(x) эта квадратурная формула точна, т.е. имеет место точное равенство

Равенство нулю следует из того, что ωn(xk)=0.

Достаточность. Пусть имеет место (15). Докажем, что квадратурная формула интерполяционного типа, построенная по корням ωn(x), точна для любого многочлена степени не выше 2n-1.

Пусть f(x) – многочлен степени не выше 2n-1. Тогда можно его представить в виде f(x)=ωn(x)q(x)+r(x), где q(x), r(x) – многочлены степени не выше n-1. Поскольку узлы квадратурной формулы одновременно являются корнями многочлена ωn(x), то во всех этих узлах выполняется соотношение

48

Тогда, применяя к функции f(x) квадратурную формулу, получим

Последнее равенство является точным в силу того, что интерполяционная формула с n узлами имеет алгебраический порядок точности не ниже, чем n-1, а степень полинома r(x) не выше, чем n-1. Учитывая (17), окончательно получаем равенство

Гаусс, рассматривая случай p(x) ≡1, предложил в качестве ωn(x) использовать полиномы Лежандра, корни которых и следует использовать в качестве узлов квадратурной формулы. В этом случае показано, что для остаточного члена справедлива следующая оценка:

В настоящее время составлены таблицы узлов и весов квадратурной формулы Гаусса при n=1, 2,…, 512.

49

3.5.Численное решение систем линейных алгебраических уравнений

Вэтой главе изучаются методы численного решения систем линейных алгебраических уравнений, т.е. численные методы линейной алгебры. Существуют два типа методов – прямые и итерационные. Эффективность прямых методов зависит от порядка системы и структуры матрицы коэффициентов. При изучении итерационных методов система уравнений трактуется как операторное уравнение первого рода Au=f и излагается общая теория итерационных методов для операторных уравнений при минимальных предположениях относительно оператора A. Общая теория позволяет доказать сходимость итераций для метода Зейделя и метода релаксации при минимальных ограничениях на оператор A.

3.5.1.Системы линейных алгебраических уравнений

3.5.1.1.Системы уравнений

Основная задача линейной алгебры – решение системы уравнений

где u=(u1,…, uN) – искомый вектор, f=(f1,…, fN) – известный вектор размерности N, A=(aij) (i, j=1,…, N) – квадратная матрица размера N*N с элементами aij.

Будем предполагать, что матрица A невырождена; detA ≠ 0, так что уравнение Au=0 имеет только тривиальное решение, и система (1) имеет единственное решение u=A-1f.

В курсе линейной алгебры решение системы (1) обычно выражают по формулам Крамера в виде отношений определителей. Для численного решения системы (1) эти формулы непригодны, т.к. они требуют вычисления N+1 определителей, для чего необходимо осуществление порядка N! арифметических операций. Даже при выборе наилучшего метода вычисление одного определителя требует такого же времени, что и решение системы линейных уравнений современными численными методами. Кроме того, вычисления по формулам Крамера часто ведут к большим погрешностям округления.

Особенность большинства численных методов для решения системы уравнений (1) состоит в отказе от нахождения обратной матрицы. Основное требование к методу решения – минимум числа арифметических действий, достаточных для отыскания приближенного решения с заданной точностью ε>0 (экономичность численного метода).

3.5.1.2. Частные случаи систем

Несложно решить систему (1) в перечисленных ниже частных случаях. Пусть матрица A – диагональная, т.е. aij=0, j ≠ i, aii ≠ 0 (i, j=1,…, N). Тогда система имеет вид aiiui=fi, откуда находим

ui=fi/aii, i=1,…, N.

Если A – нижняя треугольная матрица, т.е. aij=0 при j>i (i, j=1,…, N), aii ≠ 0,

50

Компоненты вектора u находятся последовательно при переходе от n к n+1, начиная с n=1:

Чтобы найти вектор u=(u1,…, uN), требуется 1+3+…+2N-1=N2 арифметических действий.

Если A – верхняя треугольная матрица, т.е. aij=0 при j<i, aii ≠ 0 (i, j=1,…, N),

Компоненты вектора u=A-1f определяются последовательно при переходе от n+1 к n по формулам

что требует также N2 действий.

Выбор метода и его экономичность зависят от вида матрицы A, а также от типа компьютера.

Для многих задач A является разреженной матрицей, большинство элементов которой – нули. Такие матрицы часто появляются при разностной аппроксимации дифференциальных уравнений. Элементы этой матрицы обычно вычисляются по заданным формулам, и их можно не хранить в оперативной памяти ЭВМ. Это очень важно, т.к. порядок таких матриц может достигать нескольких десятков и даже сотен тысяч.

Частным случаем разреженной матрицы является ленточная матрица; все ее ненулевые элементы находятся вблизи главной диагонали, т.е. aij=0, если i − j > l , где l<N. Отличные от

нуля элементы расположены на 2l+1 диагоналях, включая главную диагональ. Примером является

трехдиагональная матрица

Соответствующая система (1) имеет вид

−c1u1 +b1u2 = f1 ,

................................

aiui−1 −ciui +biui+1 = fi ,

.................................

aN uN −1 −cN uN = f N , i = 2,3,..., N −1.

Это разностное уравнение второго порядка, которое решается методом прогонки.

3.5.1.3. Прямые и итерационные методы