корнюшин.численные методы

61

минимизация расхода ресурсов (когда, например, они остро дефицитны) или времени, затрачиваемого на выполнение срочной работы, и т.д.

Первый и второй этапы не могут выполняться последовательно и в указанном порядке. Выбор параметров управления тесно связан с выбором показателя качества, оба эти этапа выполняются одновременно.

Третий этап – подготовка и обработка исходной информации. В настоящее время сбор и накопление необходимой для планирования и управления информации находятся в недостаточно удовлетворительном состоянии. Многие сведения неточны, иногда даже мало достоверны, некоторые данные оказываются ненужными для организации исследований, другие, необходимые для исследований, отсутствуют. Предстоит значительная работа по совершенствованию сбора, накопления и хранения исходной информации.

Четвертый этап – выбор численного метода для решения задачи математического программирования. Точные методы обычно связаны с необходимостью затратить больше труда, приближенные – менее трудоемки. Чтобы определить, какой метод решения более подходит для данной задачи, надо учитывать качество созданной математической модели и исходной информации. Если, например, модель задачи значительно упрощена, исходные данные недостаточно достоверны, то для решения задачи нет смысла применять точные, но трудоемкие численные методы.

И, наконец, пятый этап – анализ полученных результатов и составление рабочей программы. Этот этап наступает после того, как задача уже решена тем или иным методом, и оптимальный план получен. Но следует иметь в виду, что оптимальный план не всегда может быть реализован на практике. Для практического использования в него часто необходимо вносить поправки, что приводит к рабочей программе. Каков характер этих поправок? Во-первых, надо в какой-то мере учесть ограничения, которые по тем или иным мотивам не были введены в

математическую модель. Затем может оказаться, что оптимальный план привел к большому дроблению ресурсов по отдельным звеньям производственного процесса. Могут возникнуть и другие, специфические для данной задачи требования, которым полученный оптимальный план не удовлетворяет. Все это приводит к необходимости подвергнуть оптимальный план некоторому анализу. В результате обнаруживается необходимость внести поправки, после учета которых возникает рабочая программа, которую и рекомендуют к реализации.

4.6.1.2. Математическая модель задачи линейного программирования

Рассмотрим процесс образования математической модели задачи линейного программирования на нескольких конкретных примерах.

1. Задача производственного планирования

Пусть некоторое предприятие (или группа предприятий) выпускает однородную продукцию. Изготовление этой продукции связано с затратами ряда производственных факторов: различного вида сырья, энергии, топлива, работы различного типа оборудования, рабочей силы разной квалификации и т.д. Пусть этих факторов всего будет m. Присвоим им имена Ф1, Ф2,…, Фь. Каждый из них имеется в ограниченном количестве: запас факторов Ф1 составляет b1 единиц, запас фактора Ф2 составляет b2 единиц и т.д., запас фактора Фm составляет bm единиц.

Допустим далее, что предприятие располагает n отработанными технологическими способами, которые обозначим T1, T2,…, Tn (наименования разных способов). Известно, что при работе предприятия в течение единицы времени по способу Tj затрачивается aij единиц фактора Фi; в обозначении aij индекс i соответствует номеру производственного фактора, а индекс j – номеру технологического способа. Таким образом, работа предприятия в течение единицы времени по способу T1 требует затраты a11 единиц фактора Ф1, a21 единиц фактора Ф2 и т.д., am1 единиц фактора Фm.

Запишем эти данные в столбец, который можно назвать вектором производственных затрат за единицу времени при работе по способу T1:

62

a11 a21

...

ai1

...

am1

Если записать векторы производственных затрат за единицу времени рядом (для всех технологических способов), то получится прямоугольная таблица (матрица), содержащая n столбцов и m строк:

Эту таблицу называют матрицей технологических коэффициентов aij. Каждый столбец этой матрицы содержит данные о расходе всех производственных факторов при работе предприятия в течение единицы времени по способу, указанному над столбцом, а каждая строка содержит данные о расходе одного из производственных факторов, указанного сбоку, при работе в течение единицы времени по всем технологическим способам.

Допустим, что работа предприятия по способу Tj (j=1, 2,…, n) в течение единицы времени приводит к выпуску cj (j=1, 2,…, n) единиц готовой продукции, так что числа c1 , c2 ,…, cn показывают, сколько единиц готовой продукции можно получить за единицу времени по каждому из технологических способов T1, T2,…, Tn.

Если мы хотим планировать работу предприятия так, чтобы добиться максимального объема выпускаемой продукции, то в качестве параметров управления следует взять числа, показывающие, сколько времени отводится на работу по каждому из способов Tj (j=1, 2,…, n).

Предположим, что мы принимаем план (x1, x2,…, xn), т.е. назначаем работать x1 единиц времени по способу T1, x2 единиц времени по способу T2 и т.д. Тогда мы выпустим продукцию в объеме

Z=c1x1+c2x2+…+cnxn.

Величина Z, т.е. объем готовой продукции при плане x1, x2,…, xn и будет показателем качества или целевой функцией при условии, что целью планирования является получение максимального объема продукции. План x1, x2,…, xn (при этой целевой функции) будет тем лучше, чем больше величина Z, и, значит, математически задача заключается в том, чтобы найти такой план, при котором величина Z достигает максимума.

На первый взгляд, выгоднее всего планировать больше времени на тот способ Tk, для которого ck имеет наибольшее значение. Но это, конечно, не так, ибо каждый способ связан с производственными затратами, и если они велики для способа Tk, то может оказаться более выгодным применение и других способов. Ясно, что задача требует более тщательного анализа в области производственных затрат.

Поэтому рассмотрим, сколько единиц каждого из факторов будет затрачено при исполнении плана x1, x2,…, xn. Для первого фактора Ф1 это будут затраты, равные a11x1+a12x2+…+a1n xn единиц этого фактора. Для второго фактора Ф2 это будут затраты a21x1+a22x2+…+a2nxn единиц второго фактора и т.д. Но так как факторы Фi (i=1, 2,…, m) ограничены запасами bi (i=1, 2,…, m), то планировать надо так, чтобы затраты не превышали запасов, т.е. чтобы удовлетворялись неравенства:

64

расход по перевозке 1 т груза из пункта Ai в пункт Bj составляет cij руб. Требуется составить такой план перевозок, при котором обеспечивается полная разгрузка всех пунктов отправления, полное удовлетворение потребностей всех пунктов назначения и при котором суммарные расходы по перевозке были бы наименьшими.

Заметим, что в указанной постановке решение задачи возможно лишь при условии, что количество груза во всех пунктах отправления равно общей потребности во всех пунктах назначения: a1+a2+…+am= b1+b2+…+bn. Будем считать, что это условие выполняется. В этой постановке задачу называют классической транспортной задачей.

Представим математическую модель задачи.

Допустим, что принят такой план, при котором из пункта Ai в пункт Bj перевозится xij тонн (i=1, 2,…, m; j=1, 2,…, n). Тогда суммарные расходы по перевозке составят:

Z = c11 x11 +c12 x12 +... +c1n x1n + +c21 x21 +c22 x22 +... +c2n x2n +

+..................................... +

+cm1 xm1 +cm2 xm2 +... +cmn xmn .

Минимизируем это выражение:

Z = c11 x11 +c12 x12 +... +c1n x1n +

+cm1 xm1 +cm2 xm2 +... +cmn xmn → min,

т.е. потребуем, чтобы суммарные расходы по перевозке были минимальными. Это будет целевая функция задачи. Надо найти такой план xij (i=1, 2,…, m; j=1, 2,…, n), который минимизирует функцию Z.

Запишем теперь ограничения. Их здесь будет две группы. В одной выразим требование, состоящее в том, что все пункты отправления полностью разгружаются, что даст уравнения:

x11 + x12 +... + x1n = a1;

xm1 + xm2 +... + xmn = am .

Далее, выразим требование, состоящее в том, что потребности во всех пунктах назначения полностью удовлетворяются; это даст уравнения

x11 + x21 +... + xm1 = b1;

x1n + x2n +... + xmn = bn .

Наконец, следует записать, что все перевозки неотрицательны:

Таким образом, соотношения (4) – (7) составляют математическую модель транспортной задачи. Она отличается от моделей предыдущих задач, во-первых, тем, что для параметров управления, составляющих план, введены двойные индексы. Но это несущественно; можно было и здесь пользоваться одиночными индексами, но это было бы менее наглядно. Существенно то, что ограничения выражаются здесь равенствами (5) – (6), а не неравенствами, как в предыдущих задачах. Кроме того, эти равенства имеют специфическую структуру. Благодаря этому для транспортной задачи линейного программирования удается создать и специфические методы решения. Следует, однако, иметь в виду, что общее строение математической модели

65

транспортной задачи остается прежним: 1) имеется целевая функция (линейная относительно параметров управления), которую нужно оптимизировать подбором соответствующего плана; 2) имеются ограничения, выражаемые линейными зависимостями от параметров управления (от переменных, составляющих план); 3) от параметров управления требуется, чтобы они были неотрицательными.

Замечание. Транспортную задачу можно ставить на минимум времени. Она приобретает тогда несколько иную структуру, но сводится к задаче линейного программирования.

3. Расстановочная (распределительная) задача

Пусть имеется m типов автомашин, которые должны осуществлять грузоперевозки на n линиях. Пусть объем перевозок на этих линиях составляет соответственно Q1, Q2,…, Qn тоннокилометров. Известно, что если автомобиль i-го типа использовать на j-й линии, то его провозная способность составит Pij тонно-километров за весь планируемый период (если автомобиль какогото типа нельзя использовать на некоторой линии, то его провозная способность на этой линии полагается равной нулю).

Можно поставить различные оптимизационные задачи при расстановке автомобилей. Поставим, например, задачу о такой расстановке, при которой достигается минимум эксплуатационных расходов при выполнении заданных объемов перевозок на линиях. В качестве параметров управления примем доли эксплуатационного периода, отведенные для работы имеющегося парка автомобилей на тех или иных линиях. Пусть xij –доля эксплуатационного периода, отведенная для работы i-го типа автомобиля на j-й линии (i=1, 2,…, m; j=1, 2,…, n). Эти mn дробей xij (они безразмерные) и составляют план расстановки (далее будем полагать во всех обозначениях с двумя индексами: на первом месте – номер типа автомобиля, на втором – номер линии).

Если эксплуатация i-го типа автомобиля на j-й линии в течение всего периода требует расхода Rij руб., то в течение отведенного по плану времени он составит Rijxij руб. Значит, эксплуатационные расходы при намеченном плане составят сумму

Запишем математические соотношения, выражающие ограничения. Их будет две группы. В первую группу запишем требования, состоящие в том, что сумма долей планируемого периода, намеченных для работы каждого типа автомобиля на разных линиях, не может быть больше единицы:

xm1 + xm2 +... + xmn ≤1.

Затем следует математически выразить требование, предъявленное заданными объемами перевозок Q1, Q2,…, Qn на каждой линии. Получим:

P11 x11 + P21 x21 +... + Pm1 xm1 = Q1;

P1n x1n + P2n x2n +... + Pmn xmn = Qn .

Наконец, запишем, что все величины xij неотрицательны:

66

Таким образом, (8) – (11) составляют математическую модель расстановочной задачи. Она совершенно аналогична предыдущим моделям. Несущественное отличие здесь заключается в том, что часть ограничений (9) выражается неравенствами, а другая часть (10) – равенствами. Если бы Q1, Q2,…, Qn представляли нижние границы объемов перевозок на линиях (надо выполнить не меньше чем Q1, Q2,…, Qn тонно-километров на данных линиях), то ограничения (10) также выразились бы неравенствами:

P1jx1j+P2jx2j+…+Pmjxmj ≥Qj (j=1, 2,…, n).

Замечание. В литературе по линейному программированию расстановочная задача встречается под названием «обобщенная транспортная задача». Задачу, приводящую к модели (8)

– (11), называют обобщенной транспортной, т.к. структура ее ограничений (9) – (10) аналогична структуре ограничений (5) – (6). Обобщение заключается в том, что коэффициенты в группе ограничений (10) могут принимать любые значения, тогда как в группе ограничений (6) они все равны единице.

Расстановочная задача является частным случаем распределительной задачи. Распределительная задача заключается в рациональном распределении m видов изделий для изготовления их на n скооперированных предприятиях с целью, например, достижения максимума выпускаемой продукции.

4.6.1.3. Классификация задач линейного программирования

Практические вопросы, приводящие к задаче линейного программирования разнообразны. Но и приведенных выше примеров достаточно для понимания математической структуры задачи линейного программирования и ее значения на практике. Проведем классификацию этих задач.

Во-первых, различают общую задачу математического программирования и специальные задачи. При этом имеют в виду, что в некоторых задачах структура матрицы технологических коэффициентов (т.е. коэффициентов в ограничениях) имеет специфические особенности. Так, например, в транспортной задаче, если выписать столбец коэффициентов, относящихся к некоторой переменной xij , то он состоит из одних нулей, кроме i-го и (m+j)-го места, где стоят единицы. Специфично также строение матрицы технологических коэффициентов расстановочной задачи. Для таких задач можно, используя указанные особенности, создать специальные методы решения, и поэтому задачи называют специальными. Если не принимается во внимание структура матрицы технологических коэффициентов, то говорят об общей задаче линейного программирования. В первую очередь надо, конечно, изучить общую задачу, т.к. методы ее решения имеют общий характер, и они только специализируются при рассмотрении задач с особенностями.

Во-вторых, в настоящее время разработаны методы решения общей задачи линейного программирования при некоторых отклонениях от рассмотренных нами моделей или при некоторых дополнительных требованиях.

Так, разработаны методы решения общей задачи линейного программирования с учетом следующих обстоятельств:

а) коэффициенты целевой функции не являются постоянными, а меняются линейно в зависимости от некоторого дополнительного параметра, так что целевая функция имеет вид

Z=(c1+d1t)x1+(c2+d2t)x2+…+(cn+dnt)xn,

где t – дополнительный параметр (например, время). В этом случае говорят о задаче

параметрического линейного программирования;

б) ограничения, наложенные ресурсами, выражаются двусторонними неравенствами. Они имеют вид

ai ≤ai1x1+ai2x2+…+ainxn ≤bi (i=1, 2,…, m)

67

В этом случае говорят о задаче с двусторонними ограничениями. Конечно, задачу с двусторонними ограничениями можно рассматривать как обычную, записывая отдельно оба неравенства, составляющие двойное неравенство. Но так как созданы специальные приемы, упрощающие решение, то эту задачу принято выделять при изучении теории линейного программирования;

в) от решения задачи дополнительно требуют, чтобы оно выражалось в целых числах. В этом случае говорят о целочисленном программировании. Происхождение такого дополнительного требования очевидно: числа, выражающие получаемое решение, могут означать физически неделимые величины – число рейсов, число экземпляров, количество перевозочных средств (судов, вагонов, автомобилей и др.) и т.д.

Если поставить вопросы классификации задач шире, например, в объеме всего множества оптимизационных задач, то можно наметить такие области.

Прежде всего, следует отличать область линейных задач от области нелинейных задач. В последнем случае говорят о нелинейном программировании. В области нелинейного программирования в настоящее время разработаны методы решения таких задач:

а) задачи, в которых целевая функция выражается отношением двух линейных функций

Z= c1' x1 +c2' x2 +... +cn' xn . c1'' x1 +c2'' x2 +... +cn'' xn

Ктаким задачам приводит установка оптимизировать какой-то относительный (удельный) показатель качества, например: себестоимость перевозок, рентабельность продукции и т.д. В этом случае говорят о дробно-линейном программировании;

б) задачи, в которых целевая функция выражается квадратичной функцией

содержащей квадраты и попарные произведения параметров управления. Эти задачи называют задачами квадратичного программирования;

в) задачи, в которых целевая функция является так называемой выпуклой функцией от параметров управления. Не будем здесь разъяснять математического содержания понятия выпуклой функции многих переменных; в случае же одной переменной представление о выпуклой функции дает выпуклая на некотором участке кривая линия. В частности, линейная функция есть выпуклая функция. Оптимизационная задача, в которой целевая функция и ограничения описываются выпуклыми функциями от параметров управления, называется задачей выпуклого программирования.

Отметим, наконец, весьма важную для задач оптимального управления область задач динамического программирования. Само название говорит о содержании предмета. Речь идет о таких оптимизационных задачах, в которых параметры управления связаны с состоянием оптимизируемой системы на данный момент времени (на данном этапе). Эта область менее исследована, чем область статических задач, к которой относится то, что сейчас излагается в теории линейного программирования. Обычно здесь пользуются многошаговыми методами, т.е. весь рассматриваемый динамический процесс разбивают на этапы; при этом конечные результаты на одном этапе служат исходными для другого и т.д. Мы будем рассматривать модель общей задачи линейного программирования.

Выше было продемонстрировано, что ограничения задачи линейного программирования могут выражаться только неравенствами (задача производственного планирования) или только равенствами (транспортная задача). В случае, когда все ограничения выражаются неравенствами, говорят о стандартной форме задачи линейного программирования. Когда все ограничения выражаются равенствами, то говорят о канонической форме задачи линейного программирования. Встречается и смешанная задача линейного программирования (расстановочная задача).

Надо иметь в виду, что эти различия несущественны, т.к. одна форма легко преобразуется в другую. Действительно, пусть, например, задано ограничение

2x1 +3x2–x3 ≤8.

Введем дополнительную неотрицательную переменную x4 ≥ 0, такую, чтобы было

2x1+3x2–x3+x4=8.

Благодаря этому ограничение, заданное неравенством, приобрело вид равенства. В общем виде система ограничений-неравенств

ai1x1+ai2x2+…+ainxn ≤bi (i=1, 2,…, m)

68

переходит в систему ограничений-равенств ai1x1+ai2x2+…+ainxn+xn+i=bi (i=1, 2,…, m),

где дополнительные переменные все неотрицательны: xn+1 ≥0, xn+2 ≥0,…, xn+m ≥0. Эти дополнительные переменные можно считать содержащимися и в целевой функции (с нулевыми коэффициентами). При неравенствах вида “ ≥” дополнительные переменные xn+i следует вычитать из левых частей. Можно показать, что и от ограничений-равенств несложно перейти к неравенствам. Принимая это во внимание, будем исходить из стандартной формы задачи, которая особенно удобна для геометрической интерпретации.

Таким образом, будем рассматривать модель и методы решения общей задачи линейного программирования в стандартной форме, т.е. задачи, которая математически выражается так: найти те значения переменных x1, x2,…xn, при которых имеют место следующие соотношения:

Z=c1x1+c2x2+…+cnxn → max (min);

a11 x1 + a12 x2 +... + a1n xn ≤ b1; a21 x1 + a22 x2 +... + a2n xn ≤ b2 ;

......................................

am1 x1 + am2 x2 +... + amn xm ≤ bm ; x1 ≥ 0, x2 ≥ 0,..., xn ≥ 0.

4.6.2. Графический способ решения задачи линейного программирования

4.6.2.1. Геометрический смысл линейных неравенств

Задачу линейного программирования и численный метод ее решения можно истолковать геометрически. Геометрическое изображение дает ясное представление о ходе решения задачи линейного программирования и приводит к простому графическому способу решения для того случая, когда число независимых параметров управления сводится к двум.

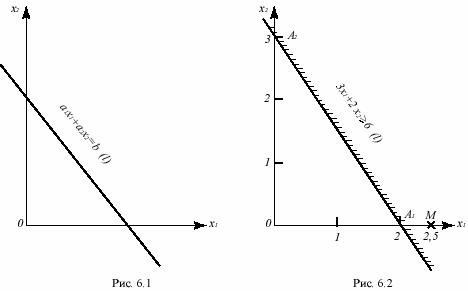
Приступая к изложению геометрической интерпретации, заметим, что прежде всего необходимо геометрически осмыслить те три звена, из которых состоит задача линейного программирования: 1) целевую функцию; 2) систему линейных ограничений; 3) требования неотрицательности искомых параметров. С этой целью будем далее рассматривать геометрические образы, возникающие на координатной плоскости двух переменных. Обычно в этом случае оси координат обозначают буквами x и y, но, имея в виду дальнейшее обобщение на многомерные пространства, будем обозначать оси координат буквами x1 и x2 (рис.6.1).

69

Как известно, линейное уравнение a1x1+a2x2=b изображается на плоскости x1Ox2 прямой линией (l), все точки которой имеют координаты x1 и x2, удовлетворяющие этому уравнению. Прямая (l) делит плоскость x1Ox2 на две полуплоскости. Для точек одной из этих полуплоскостей a1x1+a2x2<b, для точек другой a1x1+a2x2>b, а если причислять прямую (l) (границу этих полуплоскостей) к ним самим, то для точек одной из них a1x1+a2x2 ≤b, а для точек другой

a1x1+a2x2 ≥b.

Как узнать, с какой стороны от прямой (l) выражение a1x1+a2x2 (как говорят, линейная форма a1x1+a2x2) меньше, чем b и с какой стороны оно больше, чем b? Для этого достаточно в форму a1x1+a2x2 вместо x1 и x2 подставить координаты какой-нибудь определенной точки, не лежащей на прямой (l).

Например, пусть имеем неравенство 3x1+2x2 ≥6. Соответствующая прямая (l), уравнение которой есть 3x1+2x2=6, легко строится по отрезкам, которые она отсекает на осях координат. Т.к. при x2=0 будет x1=2, а при x1=0 будет x2=3, то (l) отсекает на оси x1 отрезок OA1 =2, а на оси x2 отрезок OA2=3 (рис.6.2).

С какой же стороны будет 3x1+2x2 ≥6? Для ответа на этот вопрос возьмем, например, точку

M с координатами x1=2,5; x2=0, тогда 3x1+2x2=3*2,5+2*0=7,5>6. Значит 3x1+2x2 ≥6 для точек той полуплоскости, ограниченной прямой (l), в которой лежит точка M и которая показана на рис.6.2 штриховкой вдоль прямой (l). Если в качестве точки M взять начало координат, то получим 3x1+2x2=3*0+2*0=0, откуда следует вывод о том, что 3x1+2x2 ≥6 с другой стороны от прямой (l), нежели начало координат.

Итак, всякое линейное неравенство a1x1+a2x2 ≤b ( ≥b) изображается на плоскости x1Ox2 некоторой полуплоскостью, которую можно найти, построив прямую a1x1+a2x2=b (границу этой полуплоскости) и подставив в левую часть ее уравнения координаты какой-нибудь точки, не лежащей на этой прямой.

Например, неравенство 4x1–2x2 ≤3 изображается полуплоскостью, показанной на рис.6.3 (граничная прямая отсекает на осях отрезки OA1=0,75 и OA2=-1,5, а изображающая полуплоскость расположена с той стороны от этой прямой, с которой расположена штриховка).

Пусть теперь имеем систему двух линейных неравенств:

70

a11 x1 + a12 x2 ≤ b1;a21 x1 + a22 x2 ≤ b2 .

Каждое из этих неравенств изображается некоторой полуплоскостью, а система обоих неравенств, очевидно, изображается общей частью этих двух полуплоскостей (заполняющей соответствующий угол между ними). Например, система неравенств

x1 + x2 ≤ 7;x1 +3x2 ≤ 9

изображается областью, заполняющей угол AMB (рис.6.4). В частности, важно отметить, что система неравенств

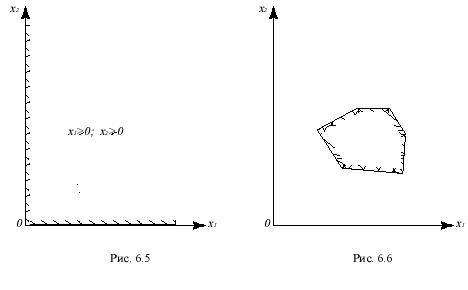
x1 ≥ 0;x2 ≥ 0,

выражающих требование неотрицательности параметров задачи линейного программирования, изображается первым квадрантом координатной плоскости x1Ox2 (рис.6.5).

Переходя к случаю системы любого числа линейных неравенств

a11 x1 + a12 x2 ≤ b1; a21 x1 + a22 x2 ≤ b2 ;

.......................

am1 x1 + am2 x2 ≤ bm ,

можно сказать, что она изображается на плоскости некоторой многоугольной областью, которая представляет собой замкнутый многоугольник (рис.6.6), но может оказаться и бесконечной (рис.6.7), и пустой (рис.6.8). Это значит, что система ограничений, налагаемых задачей линейного программирования на переменные, изображается некоторой многоугольной областью, которая во многих практически важных случаях оказывается многоугольником. Если же окажется, что эта область пустая, значит задача не имеет решения.