корнюшин.численные методы

91

Точно так же можно получить второй и третий элементы второй строки.

4.6.3.3. Опорное решение, опорный план

Вернемся к общей задаче линейного программирования (на максимум):

Z=c1x1+c2x2+…+cnxn → max;

y1 = a11 (−x1 ) + a12 (−x2 ) +... + a1n (−xn ) +b1 ≥ 0; y2 = a21 (−x1 ) + a22 (−x2 ) +... + a2n (−xn ) +b2 ≥ 0;

.............................................................

ym = am1 (−x1 ) + am2 (−x2 ) +... + amn (−xn ) +bm ≥ 0; x1 ≥ 0; x2 ≥ 0;...; xn ≥ 0.

Введем такую терминологию. Совокупность значений основных переменных x1, x2,…, xn, соответствующих какой-нибудь вершине многогранника ограничений будем называть опорным планом задачи. Совокупность значений основных переменных x1, x2,…, xn и дополнительных переменных y1, y2,…, ym, соответствующих какой-нибудь вершине многогранника ограничений,

будем называть опорным решением задачи.

Опорное решение задачи, очевидно, содержит и его опорный план, но оно шире, т.к. содержит еще и значения дополнительных переменных, т.е., в экономическом толковании, оно еще содержит числовые значения всех остатков от ресурсов, которые получаются после осуществления данного опорного плана.

Если в данной вершине достигается максимум целевой функции Z, то опорный план и опорное решение называются соответственно оптимальным планом и оптимальным решением.

Из алгебраической характеристики вершины многогранника ограничений вытекает, что все n+m чисел, составляющих опорное решение, должны быть неотрицательными и притом не менее чем n из этих чисел должны быть равны нулю.

Если пользоваться таблицами жордановых исключений и называть заключительным столбцом и заключительной строкой соответственно столбец свободных членов (помещенный в табл. 6 под 1) и строку коэффициентов целевой функции (помещенную внизу) без углового элемента (D – в нижнем правом углу), то можно легко доказать следующие две теоремы.

Теорема 1 (признак опорности решения). Если на каком-то шаге жордановых исключений оказалось, что все элементы заключительного столбца неотрицательны, то, полагая верхние переменные равными нулю, а боковые переменные равными соответствующим элементам заключительного столбца, получим некоторое опорное решение.

Для определенности изложения допустим, что мы имеем дело с четырехмерной задачей (основные переменные x1, x2, x3, x4) с тремя ограничениями (дополнительные переменные y1, y2, y3)

ипусть на каком-то шаге жордановых исключений получилась таблица, в которой элементы

заключительного столбца (см. табл. 6) β1, β2, β3 неотрицательны. Тогда, полагая верхние переменные x2=x4=y1=y3=0, получим, что боковые переменные принимают значения x1=β1, y2=β2, x3=β3, т.е. они неотрицательны. Таким образом, значения всех 4+3=7 переменных неотрицательны

ине менее чем четыре из них (x2, x4, y1, y3) равны нулю. Следовательно, x2=0, x4=0, y1=0, y3=0,

x1=β1, y2=β2, x3=β3 есть опорное решение.

Теорема 2 (признак оптимальности решения). Если на каком-то шаге жордановых исключений оказалось, что все элементы заключительного столбца и все элементы заключительной строки неотрицательны, то это означает, что достигнут максимум целевой функции; при этом оптимальное опорное решение получится, если положить верхние переменные равными нулю, а боковые переменные равными соответствующим элементам заключительного столбца. Кроме того, значение заключительного углового элемента таблицы D равно максимальному значению целевой функции (max Z).

Таблица 6

-x2 -x4 -y1 -y3 1

Действительно, т.к. элементы заключительного столбца неотрицательны, то, согласно теореме 1, указанное в формулировке решение является опорным.

Рассмотрим целевую функцию Z (снова воспользуемся табл. 6):

Z =γ1 (−x2 ) +γ2 (−x4 ) +γ3 (−y1 ) +γ4 (−y3 ) + D

Для данного опорного решения x2=x4=y1=y2=0, поэтому для него Z=D. Но так как коэффициенты γ1, γ2, γ3, γ4 неотрицательны, то для любого другого опорного плана (в котором попрежнему все переменные неотрицательны и хотя бы одна из верхних переменных отлична от

нуля) получим для целевой функции значение Z ' ≤D; следовательно, указанное в формулировке теоремы опорное решение является оптимальным и притом заключительный угловой элемент

D=max Z.

Теорема доказана.

Пример. Пусть в задаче с двумя основными и тремя дополнительными переменными на каком-то шаге жордановых исключений получились данные, представленные в табл. 7.

Таблица 7

Так как все элементы заключительного столбца положительны, то получаем опорное решение x1=6; y2=6; y3=21; y1=0; x2=0. Оно показывает, что опорный план будет следующим: x1=6; x2=0. Далее, первый ресурс исчерпан (y1=0), остаток второго ресурса равен 6 ед. (y2=6), остаток третьего ресурса равен 21 ед. (y3=21). Однако это опорное решение – не оптимальное, т.к. в заключительной строке имеется отрицательный элемент (-1).

Сделаем еще один шаг жордановых исключений с ведущим элементом, взятым в табл. 7 в рамку, т.е. поменяем ролями x2 и y2. Тогда получим табл. 8

Таблица 8

93

Теперь уже все элементы заключительного столбца и заключительной строки строго положительны. Следовательно, по второй теореме мы достигли максимума целевой функции Z. Оптимальное решение:

x1=12; x2=6; y1=0; y2=0; y3=15;

оптимальный план: x1=12; x2=6.

Остался резерв третьего ресурса в количестве 15 ед., первый и второй ресурсы исчерпаны. Максимальное значение целевой функции max Z=15.

Дополнение (признак оптимальности для задачи на минимум). Очевидно, что для задачи линейного программирования на минимум, полученный в теореме 2, признак оптимальности модифицируется следующим образом: если на каком-то шаге жордановых исключений получилась таблица, в которой все элементы заключительного столбца неотрицательны, а все элементы заключительной строки неположительны, то мы достигли минимума целевой функции; при этом оптимальное решение получается так же, как и в случае задачи на максимум, и заключительный угловой элемент дает минимальное значение целевой функции. Кроме того, задачу на минимум некоторой линейной функции Z всегда можно решить как задачу на максимум функции -Z.

4.6.3.4. Улучшение опорного плана

Итак, оптимальный опорный план (на максимум) достигается, если при неотрицательных элементах заключительного столбца оказываются также неотрицательными все элементы заключительной строки. Легко заметить, что если среди элементов заключительной строки есть хотя бы один отрицательный, то опорный план можно улучшить. Действительно, пусть, например, в заключительной строке

элемент γs<0. Целевая функция имеет такое выражение: Z=γ1( )+γ2( )+…+γs(-xs)+…+ γn( )+D, где в незаполненных скобках стоят верхние переменные, а скобка при γs для определенности заполнена переменной -xs (хотя там могла оказаться и другая переменная, но это несущественно). Для данного опорного решения значения переменных во всех скобках равны нулю (верхние переменные!), следовательно, Z=D.

Но если (для перехода из вершины A в соседнюю вершину B) двигаться по ребру, на котором xs>0, а остальные верхние переменные по-прежнему равны нулю, то целевая функция станет больше, чем в данной вершине, т.к. при

γs<0, xs>0; Z=γs(-xs)+D>D,

и, следовательно, план будет улучшаться.

Однако при увеличении xs, т.е. при движении по ребру АВ (рис. 6.23), можно продвинуться далее соседней вершины B, следовательно, можно увеличивать xs только до такого значения, при котором станет равной нулю именно та из внебазисных переменных, которая становится базисной в вершине B, например, yr.

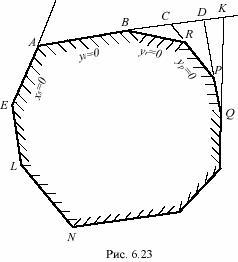
94

При вычислении нужно учесть следующее. То, что верхнюю переменную xs надо сделать внебазисной, означает, что ее надо поменять ролями с какой-то боковой переменной. С какой именно? Перевод верхней переменной xs в боковые можно осуществить с помощью очередного шага жордановых исключений, в котором s-й столбец должен быть ведущим. Но какую строку надо выбрать в качестве ведущей, чтобы не пройти мимо нужной вершины B? Чтобы ответить на этот вопрос, достаточно вспомнить, что соседняя вершина определяется не только тем, что какаято из внебазисных (боковых) переменных становится равной нулю и переходит в базисные (верхние), но и тем, что прочие внебазисные (боковые) переменные остаются неотрицательными. Рассмотрим все боковые переменные (табл. 9)

Таблица 9

Если сделать xs>0, оставив остальные верхние переменные равными нулю, то указанное требование приведет к неравенствам

y1 =α1s (−xs ) + β1 ≥ 0; y2 =α2s (−xs ) + β2 ≥ 0;

.............................

yr =αrs (−xs ) + βr ≥ 0;

.............................

ym =αms (−xs ) + βm ≥ 0.

95

Заметим, что те переменные yi, для которых коэффициенты αis ≤0, останутся

неотрицательными, каково бы ни было xs>0. Рассмотрим поэтому такое yi, для которого коэффициент αis>0. Нужно, чтобы было

yi=αis(-xs)+βi ≥0,

откуда получится, что для всех i, для которых αis>0, значение xs должно удовлетворять неравенству

xs ≤ αβi (αis>0),

is

а для этого достаточно взять xs равным наименьшему из отношений βi/αis, которые составлены для всех положительных элементов s-го столбца:

При этом значении xs получится, что r-я боковая переменная обратится в нуль:

yr=αrs(-xs)+βr=αrs(-βr/αrs)+βr=0.

Таким образом, yr станет базисной переменной (перейдет «наверх»), и вопрос о том, с какой именно боковой переменной надо поменять ролями верхнюю переменную xs, решен.

Получаем следующее правило улучшения опорного решения (плана). Если на каком-то шаге жордановых исключений среди элементов заключительной строки имеются отрицательные, то данное опорное решение можно улучшить, если сделать очередной шаг жордановых исключений, придерживаясь такой последовательности:

1)в качестве ведущего столбца выбирается любой из тех столбцов, который находится над каким-нибудь имеющим отрицательное значение элементом заключительной строки;

2)отобрав в этом столбце только элементы с положительными значениями, делим на каждый из них соответствующий элемент заключительного столбца;

3)из всех полученных отношений выбираем наименьшее и ту строку, в которой оно (наименьшее) получается, берем в качестве ведущей; на пересечении отобранных столбца и строки получаем ведущий элемент.

Пример. Используем пример предыдущего раздела (см. табл. 7). Заметим, что второй

элемент в заключительной строке (-1) отрицательный. Поэтому для улучшения плана берем второй столбец в качестве ведущего. Составляем отношения свободных членов к положительным элементам выбранного ведущего столбца; это будет 6/1 и 21/1. Минимальным оказалось отношение 6/1. Поэтому берем строку для переменной y2 в качестве ведущей. На пересечении выбранных столбца и строки получаем ведущий элемент (выделен). Сделав шаг жордановых исключений с этим ведущим элементом (см. табл. 8), мы улучшили опорное решение: в табл. 7

Z=9, а в табл. 8 Z=15.

Чтобы исчерпать вопрос об улучшении опорного решения остановимся еще на следующих аспектах:

1)не может ли случиться, что в процессе улучшения нарушится опорность решения, т.е. что при переходе по правилу улучшения к следующей таблице в заключительном столбце появятся отрицательные элементы?

2)как поступить, если в столбце над отрицательным элементом заключительной строки (который выбирается ведущим) нет ни одного положительного элемента (все элементы оказались отрицательными или нулями)?

Ответ на эти вопросы содержится в следующих двух теоремах.

Теорема 1. При переходе от таблицы к таблице по правилу улучшения опорное решение остается опорным.

Допустим, что по правилу улучшения осуществлен переход от табл. 10 к табл. 11 с ведущим элементом

96

Таблица 11

заключительного столбца новой таблицы 11. Надо показать, что если все βi ≥ 0 (i=1, 2,…, m), то и

положительный). Возьмем теперь какой-нибудь другой элемент; он получается по правилу

прямоугольника: βi' = βi −αis βr / αrs .. Возможны два случая:

1) αis ≤ 0;

так как βr/αrs ≥ 0, βi ≥ 0, то βi' ≥ βi ≥ 0;

2) αis>0;

тогда представим βi' иначе: βi' =αis (βi /αis − βr /αrs ) , и так как βr /αrs = mini βr /αis , то число

в скобке неотрицательно, а множитель αis>0; значит, и в этом случае βi' ≥ 0. Теорема доказана.

97

Теорема 2. Если на каком-то шаге жордановых исключений в столбце над отрицательным элементом заключительной строки все элементы оказались неположительными, то целевая функция может принимать сколь угодно большие значения (max Z = ∞) .

Действительно, если в s-м столбце γs<0 и αis ≤ 0 (i=1, 2,…, m), то при сколь угодно

большом значении xs>0 все значения yi=αis(-xs)+βi ≥0, так что ограничения не нарушаются, значение же целевой функции Z=γs(-xs)+D → ∞ при xs → ∞. Таким образом, если на каком-то

шаге жордановых исключений оказалась такая ситуация, как в условии теоремы 2, то вычисления обрываются, т.к. целевая функция не ограничена. Одновременно это свидетельствует о том, что область ограничений является неограниченной (а не многогранником).

В заключение отметим, что процесс улучшения плана с помощью жордановых исключений всегда требует конечного числа шагов, т.к. число вершин у многогранника ограничений конечное. При этом либо на каком-то шаге достигается оптимум целевой функции, либо эта функция неограниченна.

Пример. Требуется максимизировать функцию

Z=3x1-x2+8x3+2x4-x5+9x6

при ограничениях

−6x1 +9x2 +3x3 −2x5 − x6 ≤12;

−4x2 +3x3 −3x4 + x5 − x6 ≤ 5;

−2x1 +8x2 −5x3 +6x4 −8x5 + 4x6 ≤ 20;

−x1 −3x2 −4x3 −8x4 + 4x6 ≤10; 5x1 + x2 + 2x3 + 4x4 +9x5 +5x6 ≤ 24;

x1 ≥ 0; x2 ≥ 0; x3 ≥ 0; x4 ≥ 0; x5 ≥ 0; x6 ≥ 0.

Введем дополнительные переменные и перепишем ограничения в виде.

y1 = −6(−x1 ) +9(−x2 ) +3(−x3 ) −2(−x5 ) −(−x6 ) +12 ≥ 0; y2 −4(−x2 ) +3(−x3 ) −3(−x4 ) +(−x5 ) −(−x6 ) +5 ≥ 0; y3 = −2(−x1 ) +8(−x2 ) −5(−x3 ) +6(−x4 ) −8(−x5 ) + 4(−x6 ) + 20 ≥ 0; y4 = −(−x1 ) −3(−x2 ) −4(−x3 ) −8(−x4 ) + 4(−x6 +10 ≥ 0;

y5 = 5(−x1 ) +(−x2 ) + 2(−x3 ) + 4(−x4 ) +9(−x5 ) +5(−x6 ) + 24 ≥ 0.

Отсюда получаем исходную таблицу (табл. 12).

98

Дальнейшее решение показано в табл. 13 – 19. Справа от каждой таблицы записаны отношения элементов заключительного столбца к положительным элементам ведущего столбца. По минимуму этих отношений найден ведущий элемент, он во всех таблицах выделен.

99

100

Таблица 19

В табл. 19 заполнены только клетки заключительной строки и заключительного столбца. Так как все элементы заключительной строки табл. 19 оказались положительными, то максимум достигнут, и нет нужды вычислять прочие элементы таблицы. Оптимальное решение содержится в заключительном столбце, а именно:

x2=0,54; y4=12,36; y3=19,92; x6=3,30; x3=3,48.

Остальные переменные (верхние) все равны нулю: x1=x4=y5=y1=x5=y2=0.

Таким образом, оптимальный план будет таким:

x1=0; x2=0,54; x3=3,48; x4=0; x5=0; x6=3,30.

Оптимальное значение максимизируемой функции Zmax=57,02.